Thou cannot solve this!
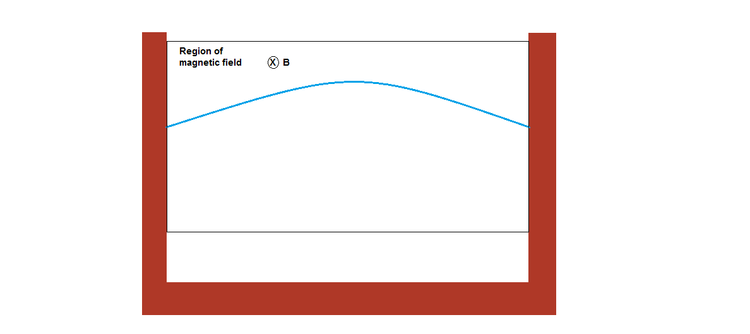 A thin conducting wire of length
, resistance
made of a non-magnetic material of uniform linear mass density
is fitted between two metal walls which are connected to each other via a thick metal strip. A tension
is maintained in the wire.
A thin conducting wire of length
, resistance
made of a non-magnetic material of uniform linear mass density
is fitted between two metal walls which are connected to each other via a thick metal strip. A tension
is maintained in the wire.
The wire is made to vibrate in its fundamental mode. At an instant when the wire is at one of the extreme positions, a uniform magnetic field of magnitude perpendicular to the plane of vibration is turned on in the area between the walls. This magnetic field damps the vibration of the wire.
Find the time taken(in seconds) for the amplitude of vibration to become half its initial value.
Details and Assumptions:
-
, , , ,
-
Assume tension to be uniform throughout the string
-
Assume that the wave oscillates in fundamental mode throughout the experiment.
You may use any computer resource to solve the problem. If you genuinely feel that this is incorrect, feel free to report.
The answer is 43.323.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we find the total energy of the wire.
When it is in mean position, potential energy =0.
At a distance x,
∣ v ∣ = 2 A ω sin ( ω t ) sin ( k x )
Clearly, asis it at mean position, cos ( ω t ) = 0
Now, kinetic energy = total energy = 2 1 ∫ 0 π / k μ ( 2 A ω sin ( k x ) ) 2 d x
We get total energy as E = μ A 2 ω 2 L
Now, induced voltage,
V = ∫ 0 L 2 A ω sin ω t sin ( L π x ) B d x
= π 4 A B ω L sin ω t
Hence, energy dissipated per second = R V 2
Also, this energy comes from loss of energy from wire, which equals − 2 μ ω 2 L A d t d A
Hence, − 2 μ ω 2 L d t d A = ( π 4 A B ω L ) 2 R sin 2 ω t
Hence, A d A = − π 2 μ R 8 B 2 L sin 2 ω t d t
Hence,we get 2 t − 4 ω sin 2 ω t = 8 B 2 L π 2 μ R ln 2
ω = 2 π f = 2 π λ v = L π μ T = 2 0 π
Using this value, we get t = 4 3 . 3 2 3