Three Aces

Let $ABC$ be the triangle in discussion, with $a=b=1$ . Let $I$ and $O$ be the incenter and the circumcenter of the triangle respectively. Denote by $r$ and $R$ the inradius and the circumradius respectively.

For the area $A$ of $\triangle ABC$ we have $A=\dfrac{abc}{4R}=sr$ where $s$ is the semiperimeter of the triangle. Thus, we get $\dfrac{1\cdot 1\cdot c}{4R}=\dfrac{1+1+c}{2}r\Leftrightarrow rR=\dfrac{c}{2c+4} \ \ \ \ \ (1)$

According to Euler's theorem in geometry it holds that $I{{O}^{2}}=R\left( R-2r \right)$ From this we get

${{R}^{2}}-2rR=1\Rightarrow {{R}^{2}}=1+2rR\overset{\left( 1 \right)}{\mathop{\Rightarrow }}\,{{R}^{2}}=1+2\dfrac{2}{2c+4}\Rightarrow R=\sqrt{\dfrac{2c+2}{c+2}} \ \ \ \ \ (2)$ On our way to build an equation for $c$ , we have

$\begin{aligned} \left. \begin{matrix} A=\dfrac{1}{2}ab\sin C \\ A=\dfrac{abc}{4R} \\ \end{matrix} \right\} & \Rightarrow \dfrac{1}{2}ab\sin C=\dfrac{abc}{4R} \\ & \overset{\left( 2 \right)}{\mathop{\Rightarrow }}\,\dfrac{\sin C}{2}=\dfrac{c}{4\sqrt{\dfrac{2c+2}{c+2}}} \\ & \Leftrightarrow 4{{\sin }^{2}}C=\dfrac{{{c}^{2}}\left( c+2 \right)}{2c+2} \\ & \Leftrightarrow 4\left( 1-{{\cos }^{2}}C \right)=\dfrac{{{c}^{3}}+2c}{2c+2} \ \ \ \ \ (3)\\ \end{aligned}$

From Cosine Rule

$\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\Rightarrow \cos C=\dfrac{2-{{c}^{2}}}{2} \ \ \ \ \ (4)$

Combining,

$\left( 3 \right),\left( 4 \right)\Rightarrow 4\left( 1-{{\left( \dfrac{2-{{c}^{2}}}{2} \right)}^{2}} \right)=\dfrac{{{c}^{3}}+2c}{2c+2}$ Rearranging, we get

$\begin{aligned} 2{{c}^{5}}+2{{c}^{4}}-7{{c}^{3}}-6{{c}^{2}}=0 & \overset{c\ne 0}{\mathop{\Leftrightarrow }}\,2{{c}^{3}}+2{{c}^{2}}-7c-6=0 \\ & \Leftrightarrow \left( c+2 \right)\left( 2{{c}^{2}}-2c-3 \right)=0 \\ & \overset{c>0}{\mathop{\Leftrightarrow }}\,c=\dfrac{1+\sqrt{7}}{2} \\ \end{aligned}$ Plugging this value in $A=\dfrac{abc}{4R}=\dfrac{c}{4\sqrt{\dfrac{2c+2}{c+2}}}$ yields $\boxed{A=\dfrac{3}{8}}$ . For the answer, $p+q=3+8=\boxed{11}$ .

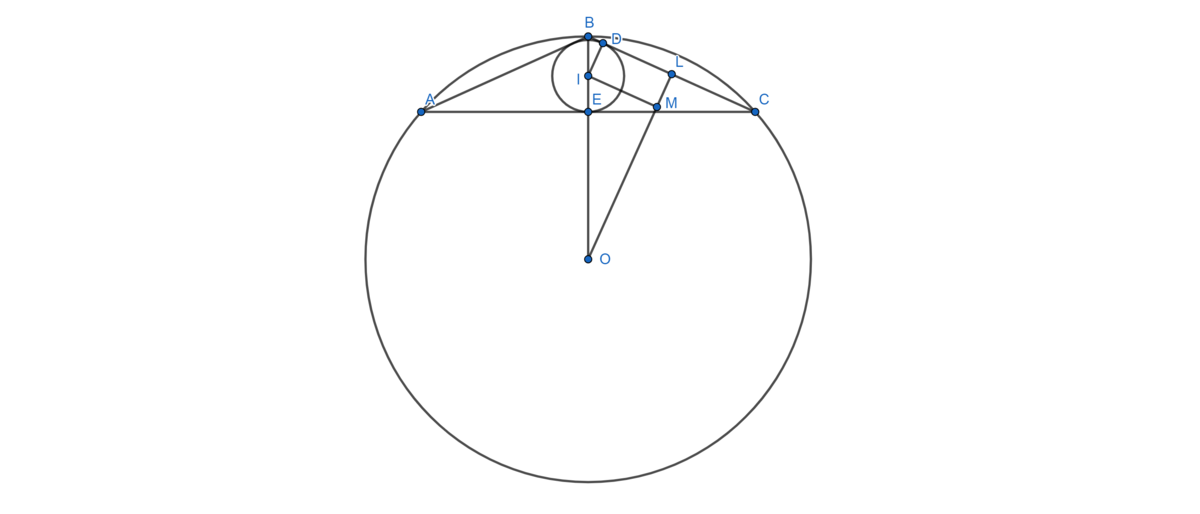
Let the incircle of $\bigtriangleup BAC$ touch sides $\overline{\rm BC}$ & $\overline{\rm CA}$ at points $D$ & $E$ respectively. Draw $\overline{\rm ID}$ & $\overline{\rm IE}$ . Drop perpendicular from $O$ on $\overline{\rm BC}$ meeting $\overline{\rm BC}$ at $L$ . Points $B$ , $I$ , $E$ & $O$ will be collinear since $\bigtriangleup BAC$ is isosceles. Draw the line containing them.

Drop perpendicular from $I$ on $\overline{\rm OL}$ meeting $\overline{\rm OL}$ at $M$ .

Observe that, in $\bigtriangleup IMO$ & $\bigtriangleup BEC$ , $\overline{\rm IO}$ $=$ $\overline{\rm BC}$ $=$ $1$ , $\angle IMO$ $=$ $\angle BEC$ & $\angle MIO$ $=$ $\angle EBC$ . Thus $\bigtriangleup IMO$ $\cong$ $\bigtriangleup BEC$ by $A$ $-$ $S$ $-$ $A$ criterion of congruency.
$\Rightarrow$ $\overline {\rm BE}$ $=$ $\overline {\rm IM}$

Let $\overline {\rm CA}$ $=$ $2a$ . $\Rightarrow$ $\overline {\rm EC}$ $=$ $\frac {1}{2}$ $\cdot$ $2a$ $=$ $a$

$\overline {\rm IM}$ $=$ $\overline {\rm DL}$ [ Since $IMLD$ is a rectangle ]

$=$ $\overline {\rm DC}$ $-$ $\overline {\rm LC}$

$=$ $\overline {\rm EC}$ $-$ $\frac {1}{2}$ $\overline {\rm BC}$ $=$ $a$ $-$ $\frac{1}{2}$

Thus, $\overline {\rm BE}$ $=$ $\overline {\rm IM}$ $=$ $a$ $-$ $\frac{1}{2}$

Applying the Pythagorean theorem on $\bigtriangleup BEC$ gives ,

$BE^2$ $+$ $EC^2$ $=$ $BC^2$

$\Rightarrow$ $(a-\frac{1}{2})^2$ $+$ $a^2$ $=$ $1$ $\Rightarrow$ $2a^2$ $-$ $a$ $=$ $\frac {3}{4}$

Therefore, area of $\bigtriangleup ABC$ $=$ $\frac {1}{2}$ $\cdot$ $\overline {\rm AC}$ $\cdot$ $\overline {\rm BE}$ $=$ $\overline {\rm EC}$ $\cdot$ $\overline {\rm BE}$ $=$ $a$ $(a-\frac{1}{2})$ $=$ $\frac{1}{2}$ $(2a^2 -a)$ $=$ $\frac{1}{2}$ $\times$ $\frac{3}{4}$ $=$ $\frac{3}{8}$

$p$ $=$ $3$ , $q$ $=$ $8$ $\Rightarrow$ $p+q$ $=$ $\boxed {11}$

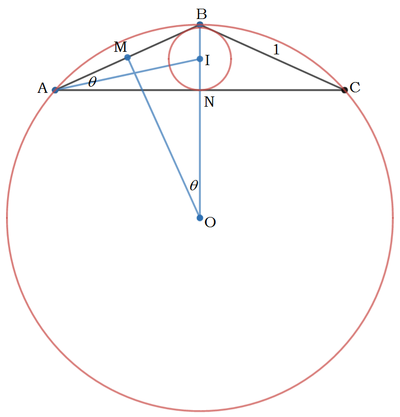
Let the isosceles triangle be $ABC$ with $AB=BC=1$ , the midpoints of $AB$ and $AC$ be $M$ and $N$ , the incenter be $I$ , and the circumcenter be $O$ . We note that $OM$ is perpendicular to $AB$ and $IO$ bisects $AC$ perpendicularly at $N$ .

We note that $\angle BAC = \angle BOM = \theta$ . Then $IN = AN \cdot \tan \dfrac \theta 2 = \cos \theta \tan \dfrac \theta 2$ . And $BO = BM \cdot \csc \theta = \dfrac 1{2\sin \theta}$ . Then we have:

$\begin{aligned} IO & = BO-BN + IN \\ 1 & = \frac 1{2\sin \theta} - \sin \theta + \cos \theta \tan \frac \theta 2 & \small \blue{\text{Let }t=\tan \frac \theta 2} \\ 1 & = \frac {1+t^2}{4t} - \frac {2t}{1+t^2} + \frac {t(1-t^2)}{1+t^2} \\ 1 & = \frac {1+t^2}{4t} - t \\ 4t & = 1 +t^2 - 4t^2 \\ \implies 3t^2 & = 1-4t \end{aligned}$

The area of $\triangle ABC$ :

$\begin{aligned} [ABC] & = \sin \theta \cos \theta = \frac {2t}{1+t^2} \cdot \frac {1-t^2}{1+t^2} = \frac {18t(1-t^2)}{(3+3t^2)^2} = \frac {18t(1-t^2)}{16(1-t)^2} = \frac {9t(1+t)}{8(1-t)} = \frac {9t+9t^2}{8(1-t)} = \frac {3-3t}{8(1-t)} = \frac 38 \end{aligned}$

Therefore $p+q = 3+8 = \boxed{11}$ .