Three circles and a triangle
Three circles with equal radii are centered at ( 1 , 0 ) , ( 0 , 0 ) , and ( 0 , 1 ) .
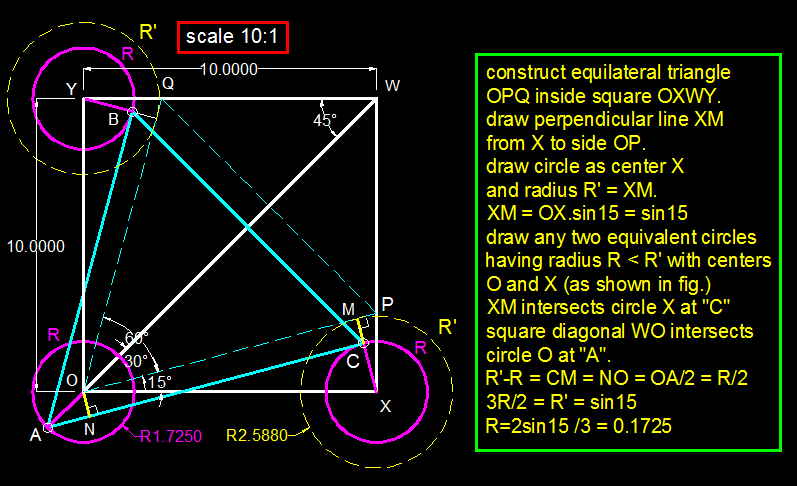
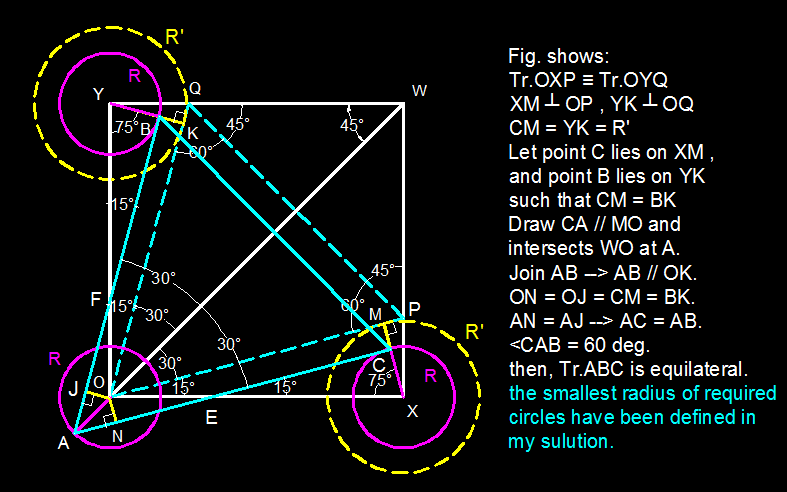
To 4 decimal places, what is the smallest radius of the circles such that we can pick a point within each circle--like A, B, C in the diagram--and connect them to form an equilateral triangle?
The answer is 0.1725.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You seem to be making some assumptions about similarity / symmetry. It's not obviously clear to me that they are justified.
Log in to reply
can u please post a solution to this problem?
F
o
r
m
i
n
i
m
u
m
,
Δ
A
B
C
m
u
s
t
f
i
t
i
n
t
h
e
g
i
v
e
n
s
y
m
m
e
t
r
y
a
b
o
u
t
y
=
x
.
∴
w
i
t
h
a
l
t
i
t
u
d
e
A
G
o
n
y
=
x
,
s
l
o
p
o
f
T
a
n
4
5
,
a
n
d
s
i
n
c
e
A
C
a
n
d
A
G
a
t
3
0
o
i
n
e
q
u
i
l
a
t
e
r
a
l
Δ
A
B
C
,
s
l
o
p
o
f
A
C
i
s
T
a
n
(
4
5
−
3
0
)
=
T
a
n
1
5
.
A
B
w
i
l
l
b
e
s
y
m
m
e
t
r
i
c
a
l
l
y
o
n
t
h
e
t
o
p
o
f
A
G
.
S
o
w
e
h
a
v
e
e
q
u
i
l
a
t
e
r
a
l
Δ
A
B
C
w
i
t
h
A
G
a
s
a
l
t
i
t
u
d
e
.
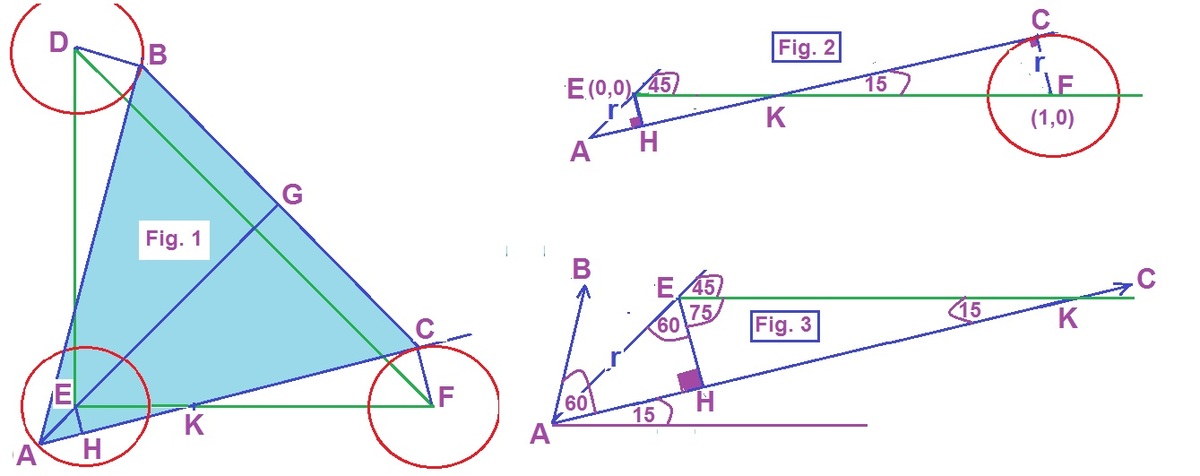
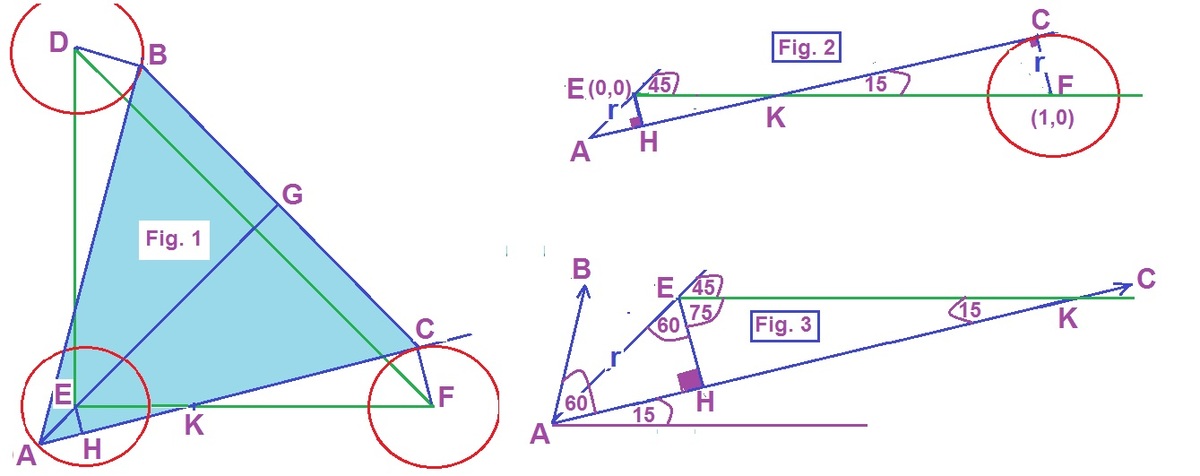
F
i
g
.
1
.
P
l
e
a
s
e
r
e
f
e
r
t
o
t
h
e
F
i
g
.
s
.
F
r
o
m
F
i
g
.
3
w
e
c
a
n
e
a
s
i
l
y
o
b
t
a
i
n
t
h
e
v
a
r
i
o
u
s
a
n
g
l
e
s
.
E
A
i
s
t
h
e
c
o
m
m
o
n
r
a
d
i
u
s
r
.
C
F
=
r
.
F
o
r
m
i
n
i
m
u
m
A
C
m
u
s
t
b
e
t
a
n
g
e
n
t
t
o
c
i
r
c
l
e
a
t
(
1
,
0
)
w
i
t
h
C
a
s
p
o
i
n
t
o
f
t
a
n
g
e
n
c
y
.
L
e
t
E
H
b
e
⊥
A
C
a
n
d
∴
E
H
∣
∣
C
F
.
I
n
3
0
−
6
0
−
9
0
Δ
E
A
H
,
E
H
=
r
/
2
.
r
t
.
Δ
E
H
C
∼
r
t
.
Δ
F
C
K
,
E
H
∣
∣
C
F
,
r
t
.
∠
,
a
n
g
l
e
1
5
o
.
∴
K
F
E
K
=
C
F
E
H
=
r
r
/
2
=
2
.
⟹
K
F
E
F
=
2
2
+
1
=
2
3
.
B
u
t
E
F
=
1
,
s
o
K
F
=
3
/
2
.
I
n
r
t
.
Δ
C
K
F
r
=
2
/
3
∗
S
i
n
1
5
=
0
.
1
7
2
5
.
Log in to reply
This is a quite tidy solution which you should add as a separate thread. It's also quite easy to resolve using numerical methods.
Log in to reply
Numerical methods? Like you're talking about some monte carlo approach? Even still, isn't that a non-rigorous solution because you didn't prove that the answer is exactly 3 2 sin 1 5 ∘ ?
How is ON = 2 O A ?
Log in to reply
<CAB = 60 deg. , CA//MO , <CAW = <MOW = 30 deg.
ON is perpendicular to AC
Tr.ONA is 30-60-90 ---> ON/OA = sin30 = 1/2
I managed to come up with a solution with a smaller radius, 0.1645. My solution has B and C on the segment joining (1, 0) and (0, 1). In fact, B and C are the intersections of that segment and the the two circles. Here are details: A is (-R, -R), B is (R/sqrt(2), 1 - R/sqrt(2)) C is (1 - R/sqrt(2), R/sqrt(2))
Log in to reply
But A is not within the circle then.
Log in to reply
Thanks for checking this for me, Geoff. You are right, A should have been (-R/sqrt(2), -R/sqrt(2)), which gives me R = 0.1895.
All these solutions seem to hold some great wisdom that eludes me. I can see that the 75 degree angle features but ended up equating sides of the triangles which results in solving the quadratic
[2 * sqrt (6) + sqrt (2) - sqrt (14 + 8 * sqrt (3))]/6.
Easy with a calculator, unwieldy with pen and paper.