Three circles, one triangle and a pink area
We have an equilateral triangle of side a (its height will be labelled as h ). If each side's midpoint is a circumcentre for a circle of radius 3 1 h , find the triangle's area that is not overlapped by any of the circles (pink area on the image below).
If m , n are both positive integers, then the area can be presented as: n m 3 − π a 2
Submit answer as: ∣ m − n ∣
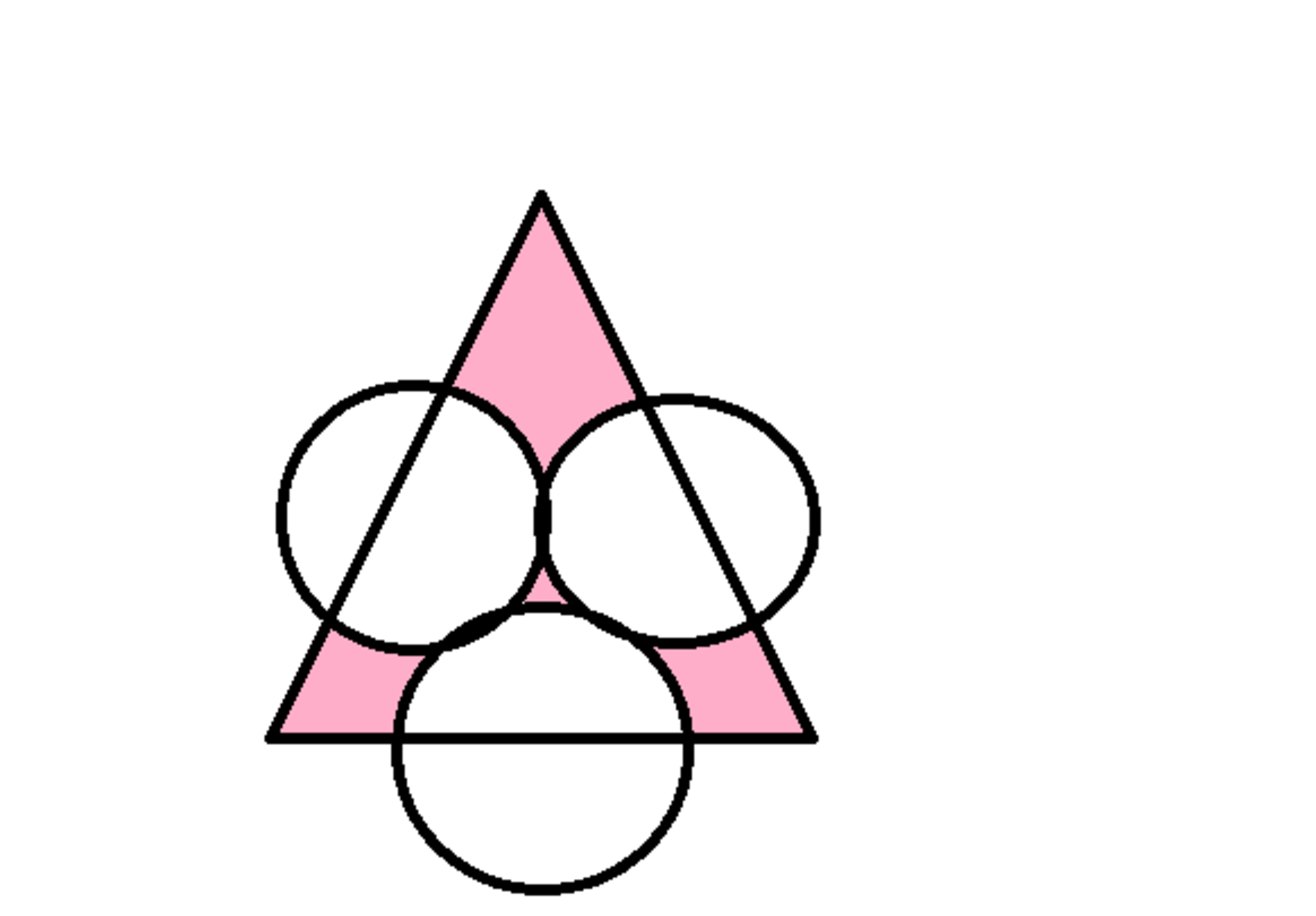
Note: keep in mind that this image is done in paint , therefore it is very inaccurate.
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
What a diagram! Nice than the solution. (Solution is also good one.)
With apology to you, I am using your diagram. Thanks. How do you draw ?
Log in to reply
No need to apologise to me. All the more, I am glad that my diagram was helpful. I use certain program called "GeoGebra". You can use that program even online. It is really good for geometry, but it can be used for other "mathematical" needs. By the way, saw your solution, up voted it. Keep up the good work!
With the help of diagram by Milan Milanic , Blue area=6 * Eqvilateral triangles side 1/3 * h = 6 ∗ 4 3 ∗ ( 3 h ) 2 = 6 ∗ 4 3 ∗ ( 2 3 ∗ 3 1 ) 2 ∗ a 2 = 8 3 ∗ a 2 . 6 Red areas are sector of a circle with 30 degrees at the center with radius h \3 = 6 ∗ 3 0 = 1 8 0 d e g r e e s , h a l f c i r c l e , = 2 π ∗ ( 3 h ) 2 = 2 π ∗ ( 2 3 ∗ 3 1 ) 2 ∗ a 2 = 2 4 π ∗ a 2 . N o t o v e r l a p p i n g a r e a = 4 3 ∗ a 2 − ( 8 3 ∗ a 2 + 2 4 π ∗ a 2 . ) = 2 4 3 3 − π ∗ a 2 . 2 1 − 3 = 2 1
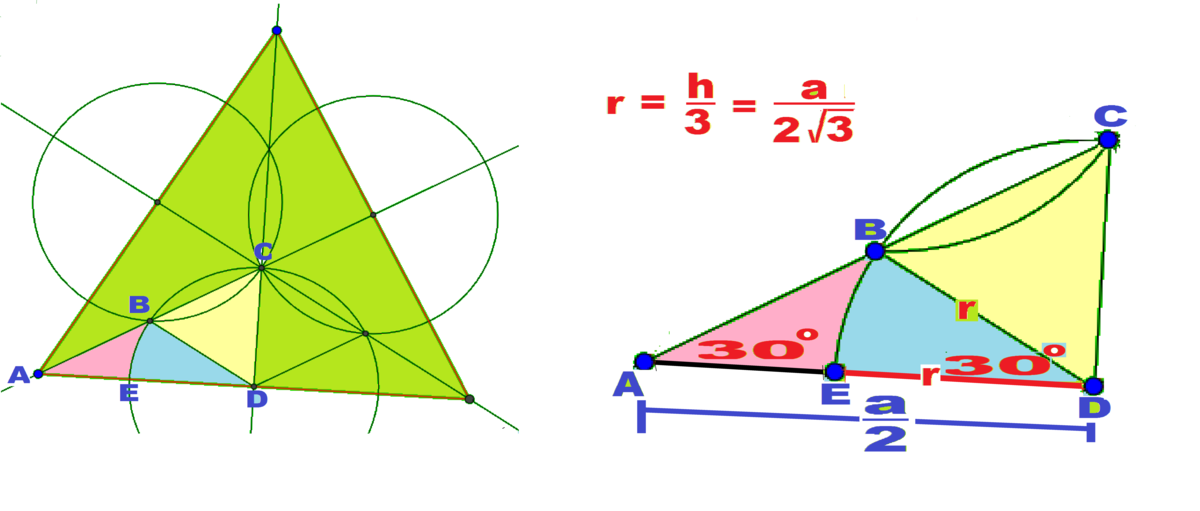
Thanks to Milan Milanic, and I got a good sketch that suggested simpler method given below.
A equilateral triangle is divided into six congruent triangles by the line that is the median, angle bisector, altitude …..One such triangle is ACD . All circles pass through centroid C. Each has a radius r.
G
i
v
e
n
h
=
2
3
a
.
∴
r
=
2
3
a
.
BCDE is the shaded part of the bottom circle in this triangle ACD.
We are interested only in the nonoverlapping pink area ABE.
Area ABE = Area triangle ACD – (sector of the circle BDE that substances 30^o
at its center.
=
2
1
∗
2
a
∗
r
S
i
n
3
0
−
π
∗
r
2
∗
3
6
0
3
0
=
4
a
∗
2
3
a
∗
2
1
−
1
2
π
∗
a
2
∗
1
2
1
=
4
8
1
∗
(
3
−
3
π
)
∴
n
o
n
o
v
e
r
l
a
p
p
i
n
g
p
i
n
k
a
r
e
a
=
6
∗
4
8
1
∗
(
3
−
3
π
)
=
2
4
3
3
−
π
∗
a
2
.
2
1
−
3
=
2
1
You mean of course: 24-3=21.
Solution:
Area of the equilateral triangle - (Red + Blue Area).
Blue Area: △ A C E = 4 1 of the Equilateral area. Therefore Blue Area = a half of the Equilateral Area. Which is 8 a 2 3
Red Area: It consists of 6 same arcs and each is 1 2 1 ( 3 6 0 ° 3 0 ° ) of whole circle. Therefore, red area = 2 1 × ( 3 1 h ) 2 × π = 2 4 π a 2 .
Not overlapped area : 2 4 3 3 − π . Answer 2 1 .