Three Circles touching each other
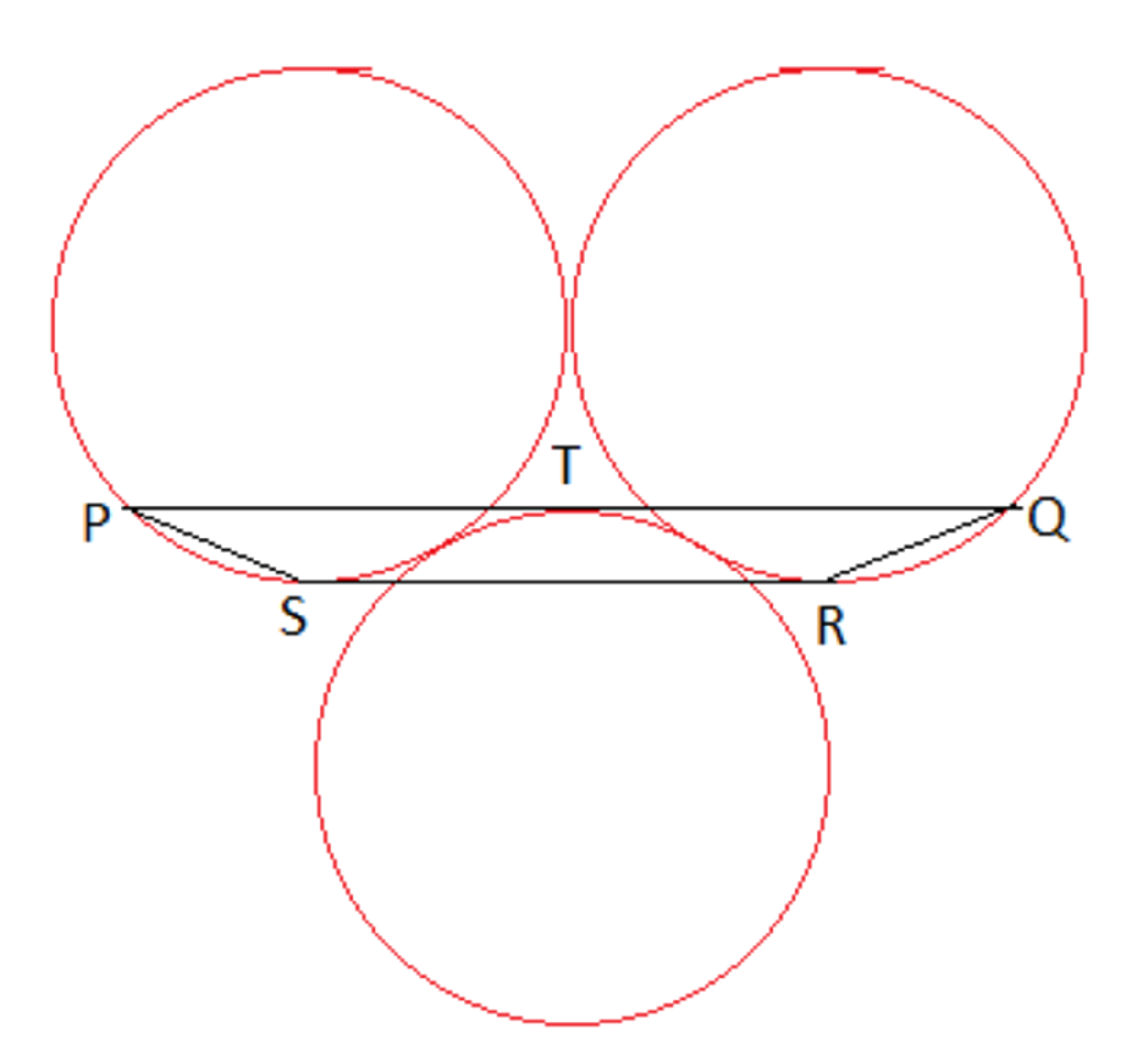
The three circles are congruent with radius . Line is tangent to the lower circle at point such that it is parallel to the line joining the centers of the above two circles. Line is a direct common tangent between the two circle shown in the figure.
If area of quadrilateral is . Then find integer nearest to
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Place the circles on a coordinate plane so that the center between the three circles is at (0, 0). Then the left circle has an equation of ( x + R ) 2 + ( y − 3 3 R ) 2 = R 2 , the right circle ( x − R ) 2 + ( y − 3 3 R ) 2 = R 2 , and the bottom circle x 2 + ( y + 3 2 3 R ) 2 = R 2 .
The y -coordinate of T can be found by solving 0 2 + ( T y + 3 2 3 R ) 2 = R 2 , which is T y = ( 1 − 3 2 3 ) R .
The x -coordinate of Q can be found by solving ( Q x − R ) 2 + ( T y − 3 3 R ) 2 = R 2 , which is Q x = ( 2 3 − 3 + 1 ) R
The x -coordinate of R is R x = R .
The y -coordinate of R can be found by solving R x 2 + ( R y + 3 2 3 R ) 2 = R 2 , which is R y = ( 3 3 − 1 ) R .
The height of the trapezoid is then h = T y − R y = ( 2 − 3 ) R .
The median of the trapezoid is then m = 2 1 ( 2 Q x + 2 R x ) = ( 2 3 − 3 + 2 ) R
The area of the trapezoid is A = ( 2 − 3 ) ( 2 3 − 3 + 2 ) R 2 = 1 0 , which solves to R 2 ≈ 1 3 . 9 1 9 ≈ 1 4 .