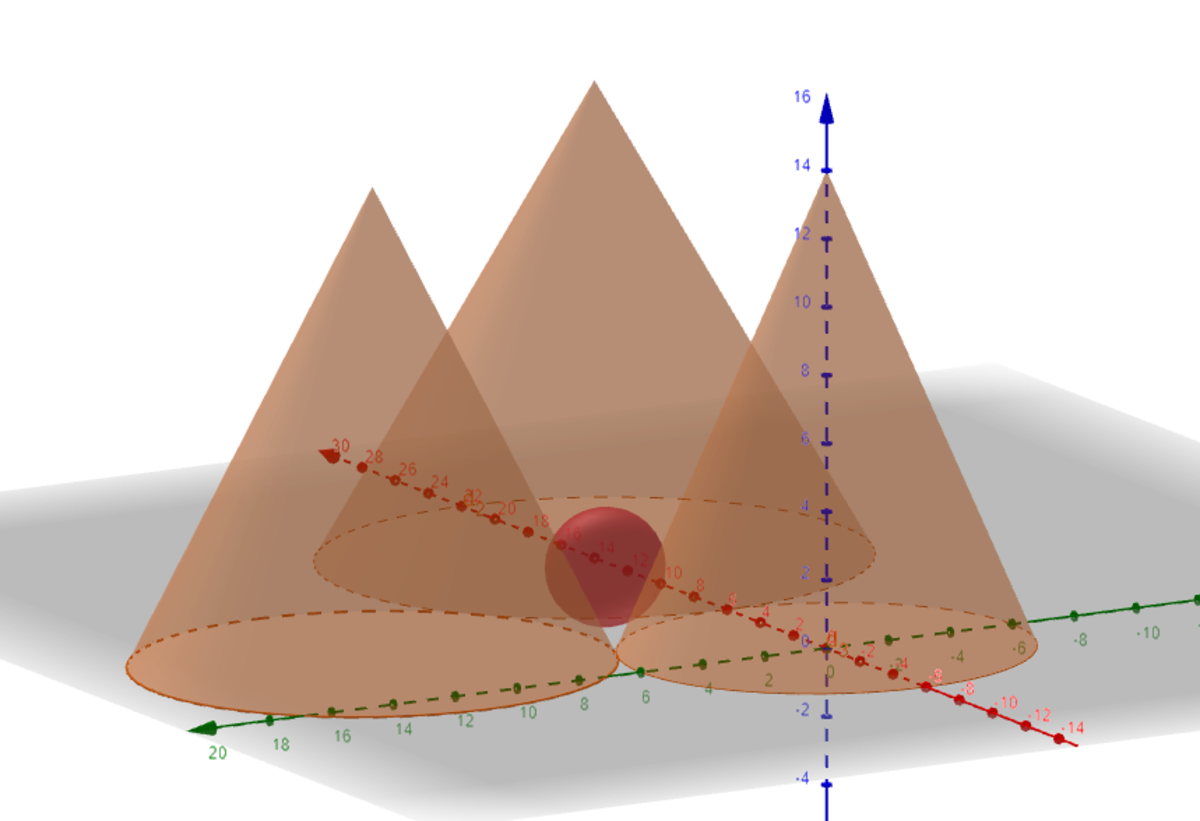
Three cones and a sphere - Unknown radius

Taking each cone separately, and viewing a cut through the cone and the sphere in a cutting plane that includes the axis of the cone and the center of the sphere, we obtain the above figure. The radius of cone base is $r$ and the radius of the sphere is $R$ . The height of the cone is $H$ . The semi-vertical angle of the cone is $\theta = \tan^{-1} \left( \dfrac{r}{H} \right)$ . Let $A$ be the apex of the cone, and $P$ be the point of tangency between the cone and the sphere. Further, let $s = | AP |$ . Finally, point $B = (x_1, y_1, z_1)$ is the center of the sphere, and $z_1 = R$ . Writing two expressions for horizontal separation and vertical separation between point $C$ (the cone base center) and point $B$ , we obtain the following:

$\sqrt{ (x_1 - C_x)^2 + (y_1 - C_y)^2 } = s \sin \theta + R \cos \theta$

$H - s \cos \theta + R \sin \theta = z_1$

Eliminating $s$ , we obtain a single equation in $x_1, y_1, z_1$ ,

$\sqrt{ (x_1 - C_x)^2 + (y_1 - C_y)^2 } = \tan \theta (H + R \sin \theta - z_1) + R \cos \theta$

Since $z_1 = R$ , this last equation becomes,

$\sqrt{ (x_1 - C_x)^2 + (y_1 - C_y)^2 } = \tan \theta H + R ( \tan \theta (\sin \theta - 1) ) + \cos \theta )$

Applying this equation for each of the three cones results in three simultaneous equations in $x_1, y_1, R$ . These solve numerically to,

$x_1 = 5.925692639, y_1= 3.984234786, R= 1.729742283 \approx \boxed{1.7297}$