Three Congruent Circles
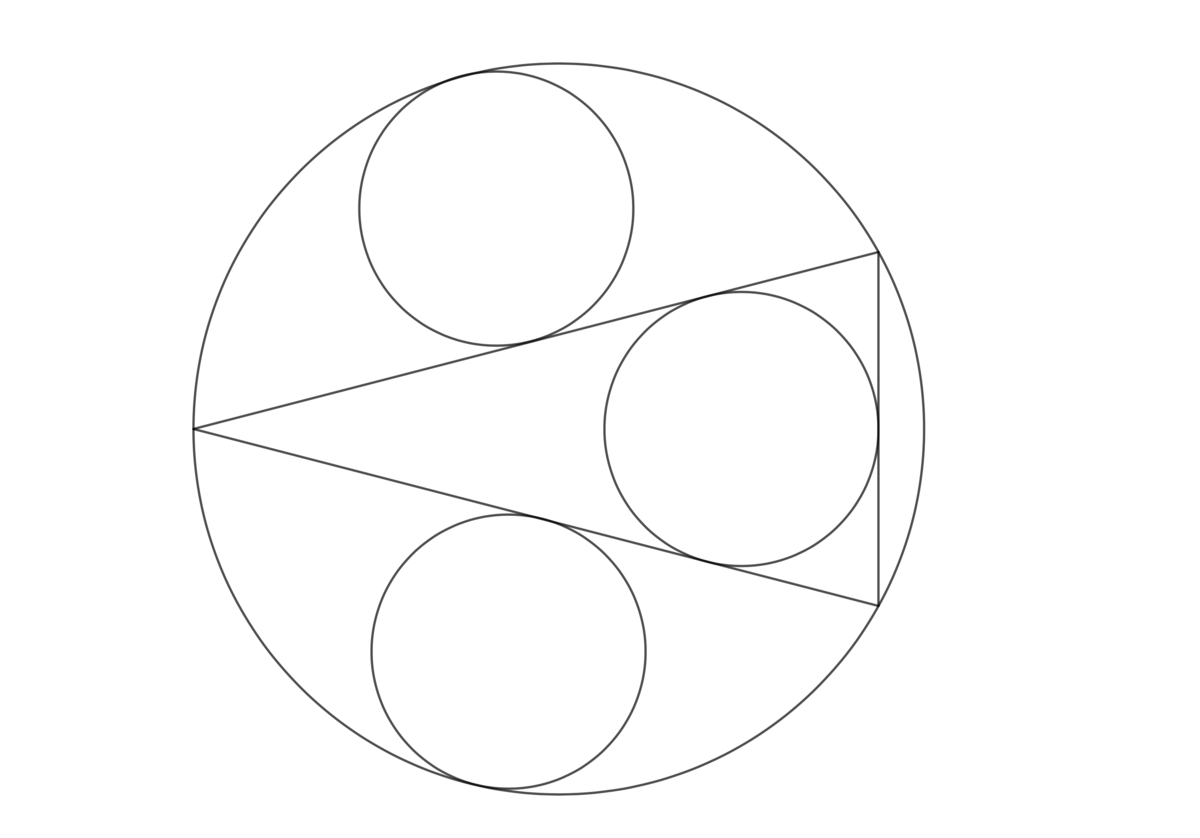
The three small circles shown in the figure are congruent. If the ratio of the radius of a small circle to the radius of the large circle can be expressed as b a , where a and b are positive coprime integers, submit a + b .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Label the diagram as below:
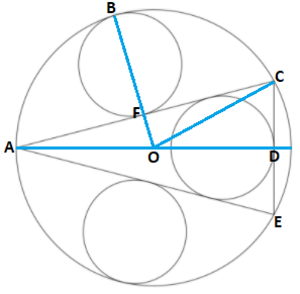
Let the radius of the large circle be 1 and the radius of the small circle be r , so that the ratio we are looking for will be r .
Also, let 2 x = ∠ C O D . Then ∠ A O C = 1 8 0 − 2 x and ∠ O C F = x .
By trigonometry on △ O C F , O F = sin x and C F = cos x .
By trigonometry on △ C O D , C D = sin 2 x and O D = cos 2 x .
From O B we know that O B = O F + F B = sin x + 2 r = 1 .
The small circle is also the incircle of △ A C E , so r = s △ A C E A △ A C E = 2 1 ( 2 A C + C E ) 2 1 ⋅ C E ⋅ A D = 2 1 ( 2 ⋅ 2 cos x + 2 sin 2 x ) 2 1 ⋅ 2 sin 2 x ⋅ ( 1 + cos 2 x ) = 2 sin x ( 1 − sin x ) .
The equations sin x + 2 r = 1 and r = 2 sin x ( 1 − sin x ) solve to r = 8 3 , so a = 3 , b = 8 , and a + b = 1 1 .
Assume radius of large circle as x and small circles as y, the sides of triangle as a,a,b. Now write the following relations from figure.
x^2-(x-2y)^2=(a^2)/4
a(x-2y)=(b/2)x
y=(b/2)[(2a-b)/(2a+b)]^0.5; inscribed circle radius
y=1
Solve using WolframAlpha get x=8/3
Answer = 8+3 =11
Vinod, I can't follow this. For example, why is the first equation true?
Log in to reply
I had more options, but chose this visual relation for a right triangle. After drawing the figure on geometry app, figure was showing the ratio as 8/3 and matching with WolframAlpha solution.
Let the radius of the large circle be 1 and the radius of the small circle be r . Then the ratio of radii is r . Let the apex angle of the isosceles triangle be θ . Let the centers of the large and small circles be O and C respectively.
We note that the length E O = 1 also equal to 2 r + sin 2 θ ⟹ r = 2 1 − sin 2 θ .
Now consider the length of the median A B :
A C + B C = A B sin 2 θ r + r r + r sin 2 θ 2 1 ( 1 − sin 2 θ ) ( 1 + sin 2 θ ) 1 − s 2 4 s 3 − s 2 − 4 s + 1 ( s − 1 ) ( s + 1 ) ( s − 4 1 ) ⟹ s ⟹ r = A O + B O = A B = 1 + cos θ = sin 2 θ + sin 2 θ ( 1 − 2 sin 2 2 θ ) = 2 sin 2 θ − 2 sin 3 2 θ = 4 s − 4 s 3 = 0 = 0 = 4 1 = 2 1 − s = 8 3 Note that r = 2 1 − sin 2 θ Let s = sin 2 θ Since θ is acute.
Therefore a + b = 3 + 8 = 1 1 .