Three Externally Tangent Circles
Geometry
Level
2
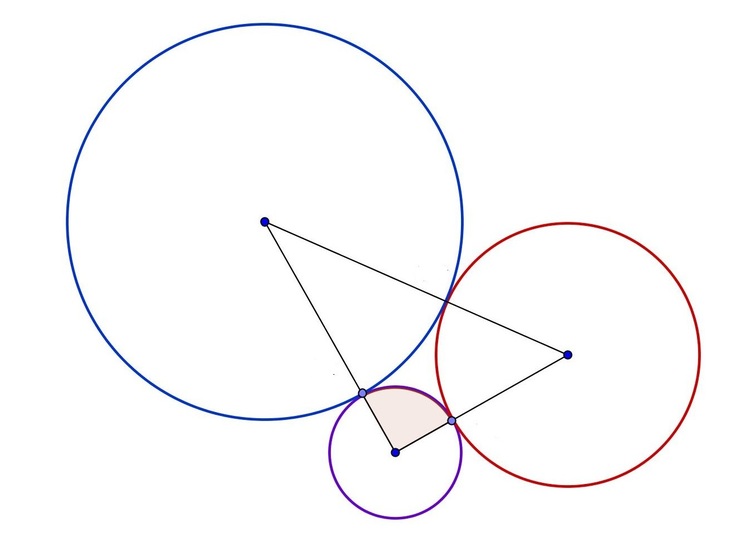The distances between any two centers of the three coplanar circles that are externally tangent to each other are 20, 24, and 28 cm. Find the area of the smallest circle.
57π cm²
49π cm²
64 π cm²
68π cm²
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Suppose r1 < r2 < r3. Then we get
r1 + r2 = 20 (1)
r1 + r3 = 24 (2)
r2 + r3 = 28 (3)
Solving the three linear equations simultaneously will yield the following results.
r1 = 8cm, r2 = 12cm and r3 = 16cm.
The area of the smallest circle is therefore,
A = π(8)² = 64 π cm²