Three externally touching circles tangent to two paralle lines by HCR
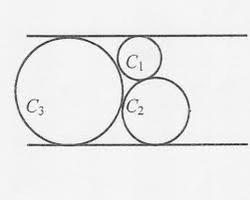 Three externally touching circles C1, C2 & C3 are tangent to two parallel lines (as shown in the figure above). The radii of circles C1 & C2 are 6 & 12 units respectively. If the distance between the parallel tangent lines is a√b where a & b are positive integers (b is square free) find out the value of a+b
Three externally touching circles C1, C2 & C3 are tangent to two parallel lines (as shown in the figure above). The radii of circles C1 & C2 are 6 & 12 units respectively. If the distance between the parallel tangent lines is a√b where a & b are positive integers (b is square free) find out the value of a+b
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
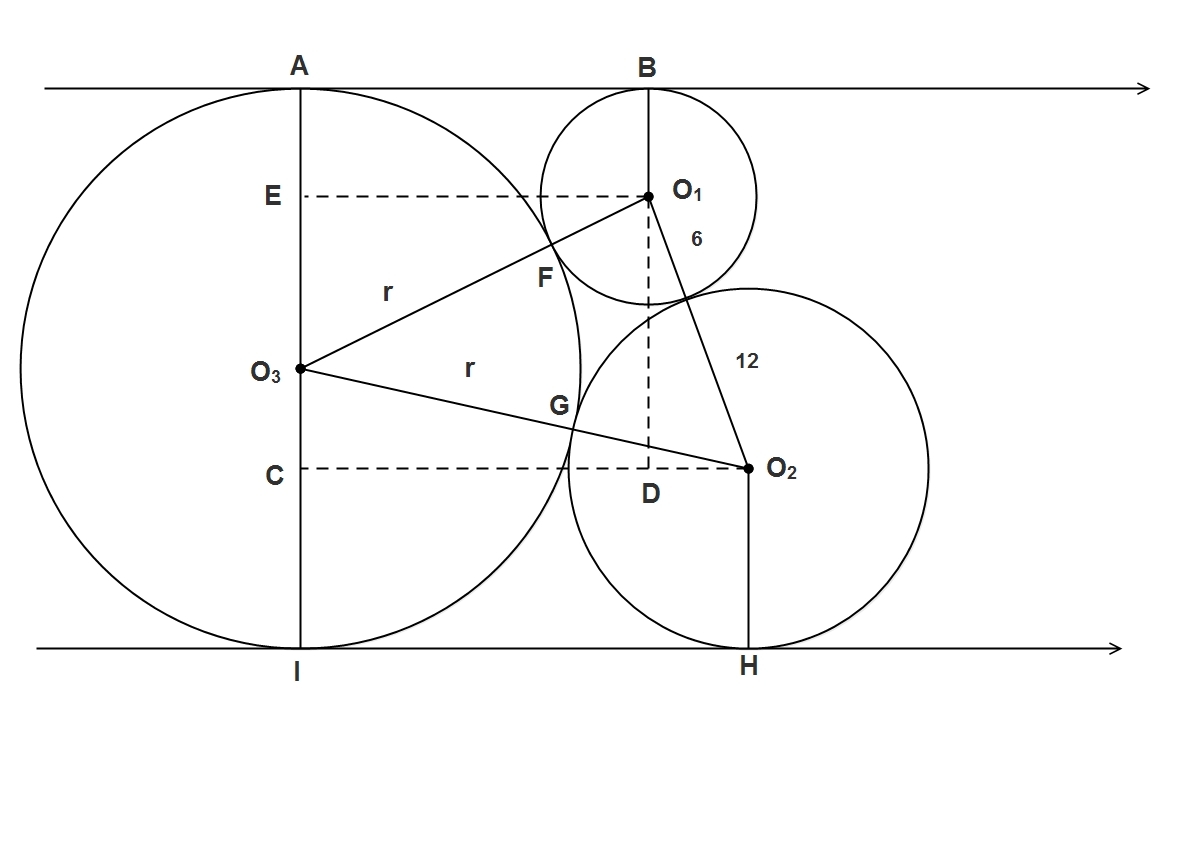

Excellent diagram, Nibedan.
@nibedan mukherjee : Here is a greatly helpful link for general formula: Three externally touching circles by HCR
Log in to reply
Thanks! for the info @mukul avasthi . Unfortunately I know this, but I have tried to solve it using the most basic theorem used in Euclidean geometry! no offense! cheers!
Let the centers of circles C 1 , C 2 , C 3 be P 1 , P 2 , P 3 , respectively, and let the radius of C 3 be r . We are thus looking for 2 r .
Draw lines L 1 and L 2 parallel to the given two parallel lines through P 1 and P 2 , respectively, and lines V 2 and V 3 perpendicular to the given two parallel lines through P 2 and P 3 , respectively.
Now let L 1 intersect V 3 and V 2 at A and B , respectively, and L 2 intersect V 3 and V 2 at D and E , respectively.
Then Δ A P 1 P 3 is a right triangle with hypotenuse P 1 P 3 length 6 + r and vertical leg A P 3 length r − 6 . By Pythagoras we then have that horizontal leg A P 1 has length
( 6 + r ) 2 − ( r − 6 ) 2 = 2 4 r .
Next, we see that Δ D E P 3 is a right triangle with hypotenuse E P 3 length 1 2 + r and vertical leg D P 3 length r − 1 2 . By Pythagoras we then have that horizontal leg D E has length
( 1 2 + r ) 2 + ( r − 1 2 ) 2 = 4 8 r .
Finally, we see that Δ B E P 1 is a right triangle with hypotenuse E P 1 length 1 8 , vertical leg B E length 2 r − 1 8 and horizontal leg B P 1 length
∣ D E ∣ − ∣ A P 1 ∣ = 4 8 r − 2 4 r = ( 2 − 1 ) 2 4 r .
By Pythagoras, we then have that
1 8 2 = ( 2 r − 1 8 ) 2 + ( 2 − 1 ) 2 ( 2 4 r )
⟹ 1 8 2 = 4 r 2 − 7 2 r + 1 8 2 + ( 3 − 2 2 ) ( 2 4 r )
⟹ 4 r 2 − 4 8 2 r = 0 ⟹ 4 r ( r − 1 2 2 ) = 0 .
Now since r = 0 we see that r = 1 2 2 , and thus the distance between the original two parallel lines is 2 4 2 , giving us a + b = 2 4 + 2 = 2 6 .
https://brilliant.org/problems/find-the-areaonly-your-logic-can-help-you/?group=3UHxOzwinQpA&ref_id=384997
PLEASE TRY TO DO THIS AWSOME PROBLEM TOO..post a solution if you get......................i am waiting for an awesome solution that i made while creating this problem
In general, if r 1 a n d r 2 are radii of small circles C 1 & C 2 then the radius R of largest circle C 3 inscribed in a rectangle , is given by the general formula
R = 2 r 1 r 2
As per given problem, setting r 1 = 6 , r 2 = 1 2 the radius of largest circle is given as R = 2 6 ⋅ 1 2 = 2 7 2 = 1 2 2
hence the distance between the parallel lines 2 R = 2 ⋅ 1 2 2 = 2 4 2 = a b
∴ a + b = 2 4 + 2 = 2 6