Three Incircles and a Rectangle
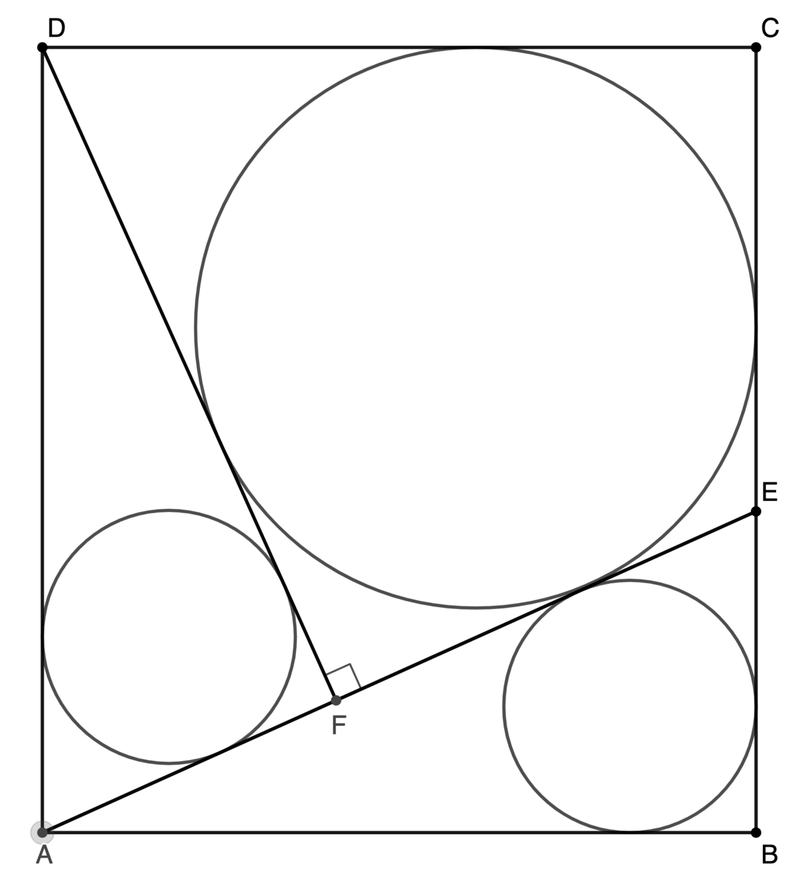
Rectangle A B C D has integer sides. E is chosen on B C so that the incircles of △ A B E and △ A F D are congruent. A E is perpendicular to D F . If the radius of the incircle of the quadrilateral F E C D is 4 3 , what is the minimum area of the rectangle?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
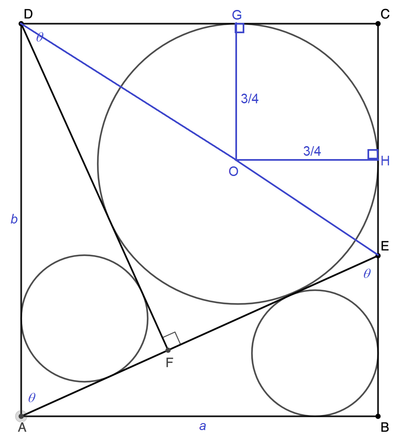
Let A B = C D = a and B C = D A = b . We note that △ A D F and △ A B E are congruent. Let the center of the incircle of F E C D be O , O G = 4 3 and O H = 4 3 be perpendicular to C D and B C respectively, and ∠ C D F = ∠ D A F = ∠ A E B = θ . Then we have:
C D a a ⟹ t = D G + G C = 4 3 cot 2 θ + 4 3 = 4 3 ( t 1 + 1 ) = 4 a − 3 3 Let t = tan 2 θ
From the congruent triangles,
b ⟹ 6 b = a csc θ = a ⋅ 2 t 1 + t 2 = a ( t 1 + t ) = 2 a ( 3 4 a − 3 + 4 a − 3 3 ) = 4 a 2 − 3 a + 4 a − 3 9 a
Putting in integer values for a it is found that the smallest integer solution is when a = 3 , then b = 5 and the area of the rectangle is a b = 1 5 .
A technicality, but I believe that to show that 6 b is an integer you also need to show that 4 a − 3 9 is also not a factor of a 1
b only increases with a when b > 1 . 2 4 3 .
You could split up 4 a − 3 9 a to 4 9 + 4 ( 4 a − 3 ) 2 7 , so that 6 b = 4 a 2 − 3 a + 4 a − 3 9 a becomes 2 4 b = 1 6 a 2 − 1 2 a + 9 + 4 a − 3 2 7 . Then from there you just need to test factors of 2 7 .
Since △ A B E ∼ △ D F A by AA similarity, and their incircles are congruent, △ A B E ≅ △ D F A .
Let a = A F = B E , b = F D = A B , and c = A D = A E , and extend D C and A E to meet at G :
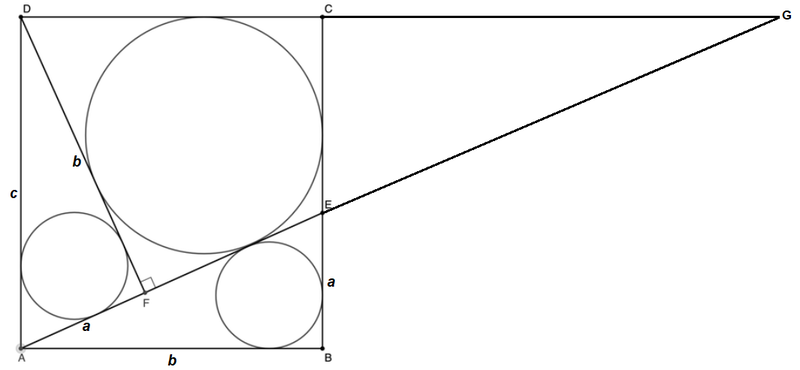
Then △ G F D ∼ △ D F A by AA similarity, G F = F D ⋅ A F F D = b ⋅ a b = a b 2 and G D = F D ⋅ F D A D = b ⋅ a c = a b c .
The inradius r of right △ G F D is r = 2 1 ( F D + G F − G D ) = 2 1 ( b + a b 2 − a b c ) = 4 3 .
By the Pythagorean Theorem, a = c 2 − b 2 , and substituting this into 2 1 ( b + a b 2 − a b c ) = 4 3 and rearranging gives ( 4 b − 3 ) ( 2 4 c − 1 6 b 2 + 1 2 b − 9 ) = 2 7 .
Since rectangle A B C D has integer sides, b and c must be positive integers, which means 4 b − 3 is a positive integer, and from the equation above, 4 b − 3 must also be a factor of 2 7 , so either 4 b − 3 = 1 , 4 b − 3 = 3 , 4 b − 3 = 9 , or 4 b − 3 = 2 7 .
If 4 b − 3 = 1 , then b = 1 , but c = 3 5 , a non-integer.
If 4 b − 3 = 3 , then b = 2 3 , a non-integer.
If 4 b − 3 = 2 7 , then b = 2 1 5 , a non-integer.
If 4 b − 3 = 9 , then b = 3 and c = 5 , both integers.
Therefore, b = 3 , c = 5 , and the area of rectangle A B C D is 1 5 .
Suppose that A D = a and A B = b , where a > b are positive integers. Then A F = B E = a 2 − b 2 , D F = D C = b and F E = C E = a − a 2 − b 2 . Thus the quadrilateral C D F E has an incircle with radius r , where 2 1 ( b + a − a 2 − b 2 ) r = 2 1 b ( a − a 2 − b 2 ) Since r = 4 3 we deduce that 3 ( a + b − a 2 − b 2 ) ( 4 b − 3 ) a 2 − b 2 ( 4 b − 3 ) 2 ( a 2 − b 2 ) 8 b 3 − 1 2 b 2 − 1 2 a b + 9 a + 9 b = 4 b ( a − a 2 − b 2 ) = 4 a b − 3 a − 3 b = ( 4 a b − 3 a − 3 b ) 2 = 0 From this it follows that b = 3 c is divisible by 3 , and hence that 0 a = 2 4 c 3 − 1 2 c 2 − 4 a c + 3 c + a = 4 c − 1 2 4 c 3 − 1 2 c 2 + 3 c = 6 c 2 − 4 c − 1 3 c ( 2 c − 1 ) and hence 4 c − 1 must divide 3 c ( 2 c − 1 ) . SInce 4 × c − ( 4 c − 1 ) = 1 , c and 4 c − 1 are coprime. Since ( 4 c − 1 ) − 2 ( 2 c − 1 ) = 1 , 2 c − 1 and 4 c − 1 are coprime. Thus we deduce that 4 c − 1 must divide 3 , and hence that c = 1 .
Thus the only solution is given by a = 5 , b = 3 , and so the area of the rectangle is 1 5 .