Three inside Ten
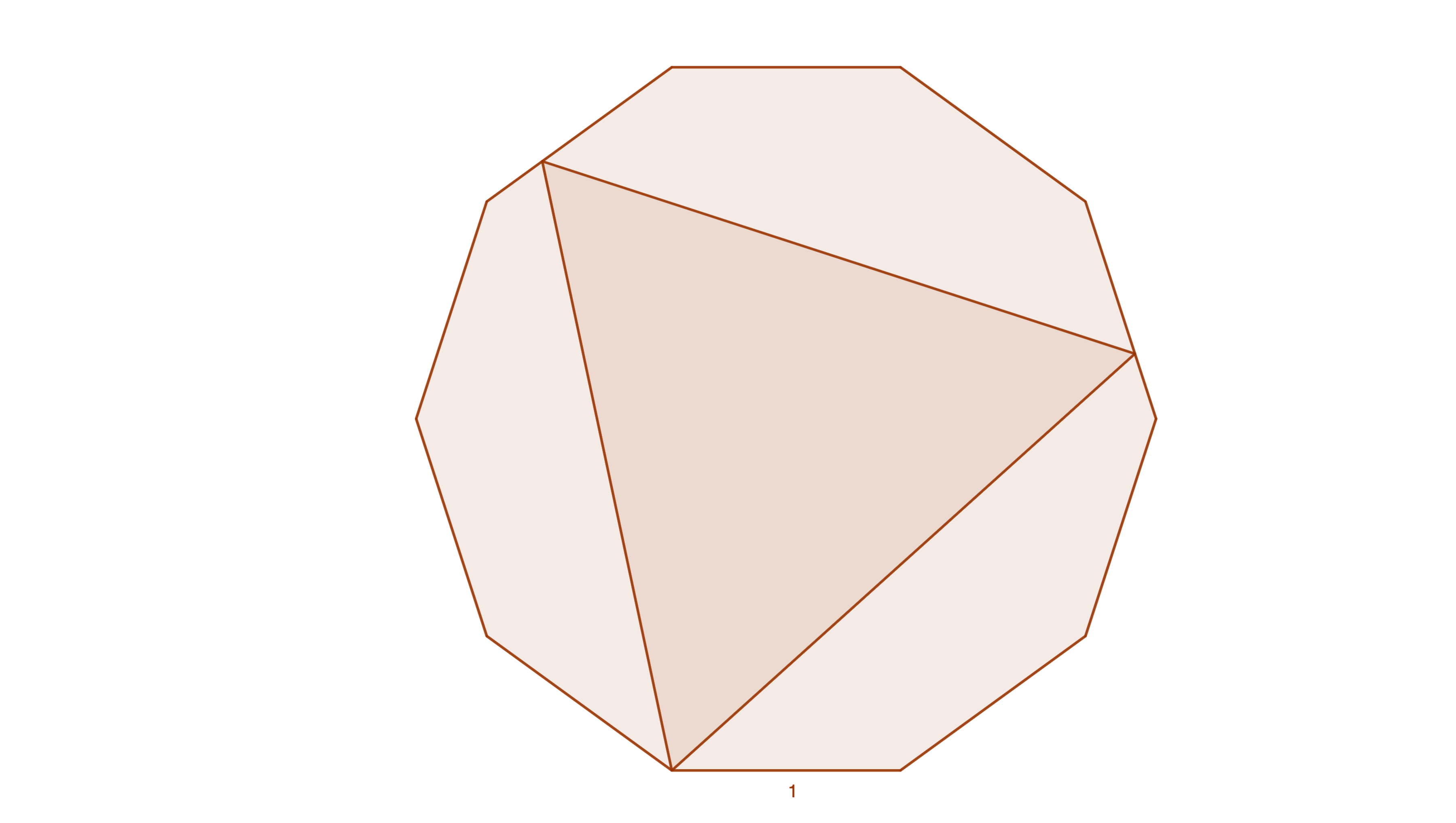
An equilateral triangle is inscribed in a regular decagon of side length 1 such that a triangle vertex and decagon vertex are coincident. What is the shortest distance between one of the other triangle vertices and a vertex of the decagon? Find a closed-form of this distance, , convert it to decimal, and submit .
The answer is 29955714.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The closest decagon vertex to E is either D or the other vertex from the decagon side. Let E D = s .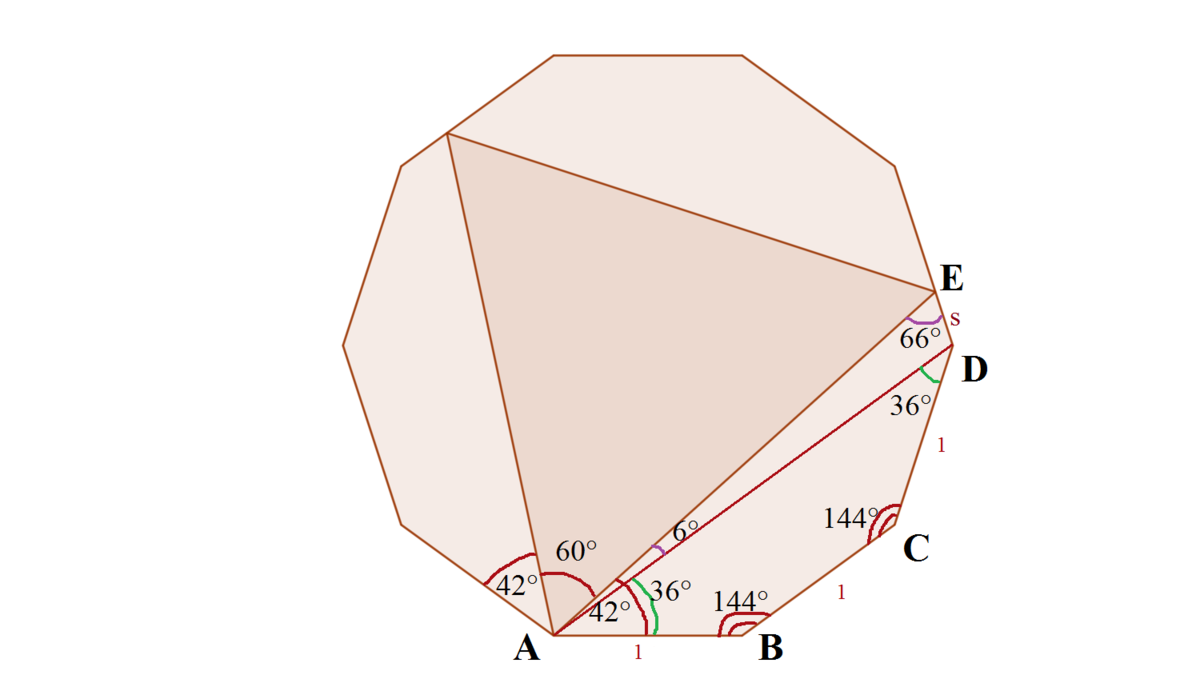 It's not hard to find that the central angle of a regular decagon is
1
0
2
π
=
5
π
, from where we find the internal angle to be
π
−
5
π
=
5
4
π
=
1
4
4
o
. From the symmetry at vertex
A
we have
2
∠
B
A
E
+
6
0
o
=
1
4
4
o
and so
∠
B
A
E
=
4
2
o
. The sum of the angles of the pentagon
A
B
C
D
E
is
5
4
0
o
, from which we find
∠
A
E
D
=
6
6
o
.
Now let's connect points
A
and
D
. Obviously
A
B
C
D
is a trapezoid with equal legs of a unit length, so it's an isosceles trapezoid. Then
∠
B
A
D
=
∠
C
D
A
=
3
6
o
. Also
∠
E
A
D
is
6
o
. Drawing heights from
B
and
C
to the base
A
D
splits the trapezoid to two congruent right triangles and a rectangle. Then it's easily found that
A
D
=
1
+
2
cos
3
6
o
Consider
△
A
D
E
. The Law of Sines gives:
sin
6
6
o
A
D
=
sin
6
o
s
Substituting for
A
D
and rearranging results in:
s
=
sin
6
6
o
sin
6
o
(
1
+
2
cos
3
6
o
)
≈
0
.
2
9
9
5
5
7
1
4
5
5
5
5
3
9
1
8
7
s
<
0
.
5
so it will be the desired distance. Note that the original drawing gives the intuition that
s
=
D
E
is indeed the desired length but sometimes this can be misleading. Finally:
⌊
1
0
8
s
⌋
=
2
9
9
5
5
7
1
4
It's not hard to find that the central angle of a regular decagon is
1
0
2
π
=
5
π
, from where we find the internal angle to be
π
−
5
π
=
5
4
π
=
1
4
4
o
. From the symmetry at vertex
A
we have
2
∠
B
A
E
+
6
0
o
=
1
4
4
o
and so
∠
B
A
E
=
4
2
o
. The sum of the angles of the pentagon
A
B
C
D
E
is
5
4
0
o
, from which we find
∠
A
E
D
=
6
6
o
.
Now let's connect points
A
and
D
. Obviously
A
B
C
D
is a trapezoid with equal legs of a unit length, so it's an isosceles trapezoid. Then
∠
B
A
D
=
∠
C
D
A
=
3
6
o
. Also
∠
E
A
D
is
6
o
. Drawing heights from
B
and
C
to the base
A
D
splits the trapezoid to two congruent right triangles and a rectangle. Then it's easily found that
A
D
=
1
+
2
cos
3
6
o
Consider
△
A
D
E
. The Law of Sines gives:
sin
6
6
o
A
D
=
sin
6
o
s
Substituting for
A
D
and rearranging results in:
s
=
sin
6
6
o
sin
6
o
(
1
+
2
cos
3
6
o
)
≈
0
.
2
9
9
5
5
7
1
4
5
5
5
5
3
9
1
8
7
s
<
0
.
5
so it will be the desired distance. Note that the original drawing gives the intuition that
s
=
D
E
is indeed the desired length but sometimes this can be misleading. Finally:
⌊
1
0
8
s
⌋
=
2
9
9
5
5
7
1
4