Three level maxima

Algebra Level pending

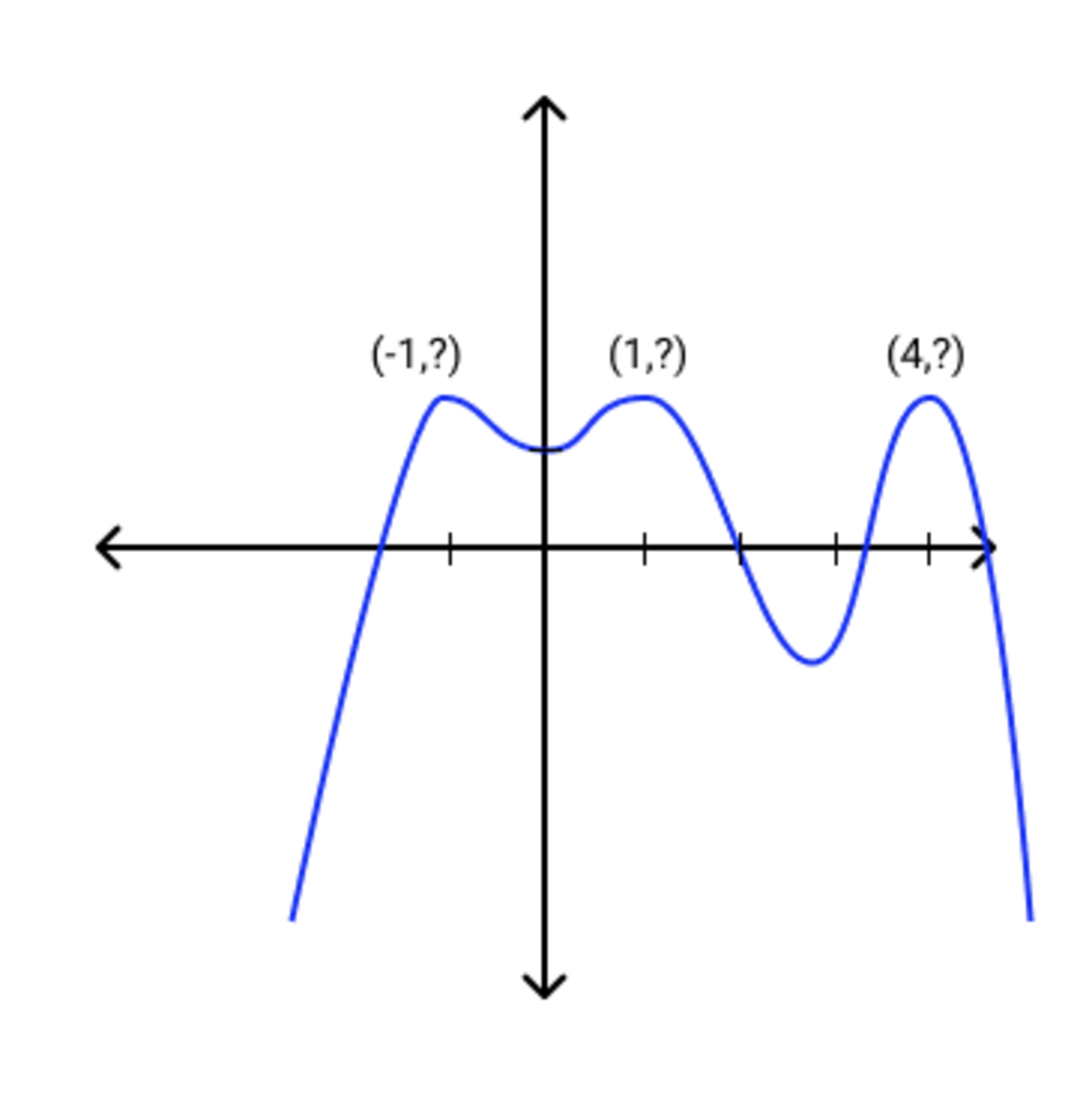
A $6^\text{th}$ degree polynomial has $y$ -intercept $1,$ and attains its absolute maximum value when $x$ is $-1,1,$ and $4$ . One of its $x$ -intercepts is $2$ . Determine the polynomial's maximum value.

1.8

1.6

1.4

1.5

1.2

1 solution

Michael Nasti
Mar 17, 2017

Call the polynomial $P(x)$ and its maximum value $k$ . Define a new 6th degree polynomial $Q(x)=P(x)-k$ . Then $Q(x)$ is tangent to the $x$ -axis at $-1,1,$ and $4$ so it has double roots at each of these values and thus has the form $Q(x) = a(x+1)^2(x-1)^2(x-4)^2$ for some constant $a$ .

This means $P(x) = a(x+1)^2(x-1)^2(x-4)^2+k$ and using the given intercepts $(0,1)$ and $(2,0)$ we get two equations:

$P(0)=1=16a+k \\ P(2)=0=36a+k$

Solving yields $a=\frac{-1}{20}$ and $k=\frac{9}{5}=1.8$

Why not Q(x) can be lke this

$Q(x)=a(x+1)(x-1)(x-4)^4 + k$

Kushal Bose - 4 years, 2 months ago

This is where the fact that the graph of $Q(x)$ is tangent to the $x$ -axis comes in. If a polynomial has a root of odd multiplicity, the graph passes through the $x$ -axis at that $x$ value, while if the root has even multiplicity, the graph touches but then remains on the same side of the $x$ -axis there. One way to think about this is a factor of the form $(x-r)^n$ will change signs as $x$ increases from less than $r$ to greater than $r$ when $n$ is odd, but have the same sign when $n$ is even.

So since the multiplicity of each root must be even, and they must add up to $6$ , each root must have multiplicity $2$ .

Michael Nasti - 4 years, 2 months ago

Okk I got it

Kushal Bose - 4 years, 2 months ago

Three level maxima

1 solution

0 pending reports