Three Lines, Three Circles
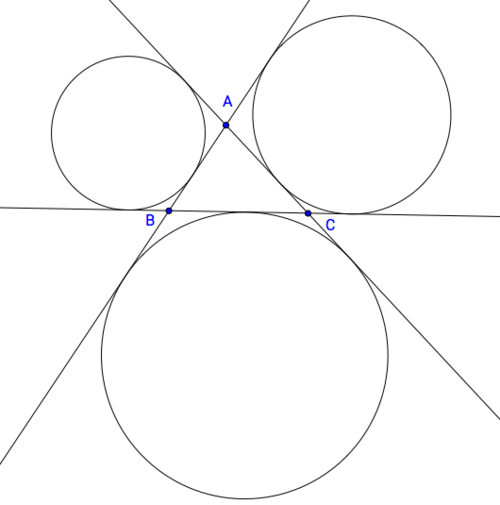 Lines
l
,
m
,
n
in the same plane are such that
l
∩
m
=
A
,
m
∩
n
=
B
,
l
∩
n
=
C
,
and
A
=
B
=
C
.
The three circles that are tangent to
l
,
m
,
and
n
but not in the interior of
A
B
C
have radii
3
,
4
,
and
5
.
If
A
B
+
B
C
+
C
A
=
p
q
,
for positive integers
p
and
q
such that
q
is not divisible by the square of any prime, find
p
+
q
.
Lines
l
,
m
,
n
in the same plane are such that
l
∩
m
=
A
,
m
∩
n
=
B
,
l
∩
n
=
C
,
and
A
=
B
=
C
.
The three circles that are tangent to
l
,
m
,
and
n
but not in the interior of
A
B
C
have radii
3
,
4
,
and
5
.
If
A
B
+
B
C
+
C
A
=
p
q
,
for positive integers
p
and
q
such that
q
is not divisible by the square of any prime, find
p
+
q
.
Notes:
Assume that such a configuration described in the problem is possible.
a ∩ b means the intersection of lines a and b .
See the next problem here .
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wish You a Merry Christmas and a Happy New Year
Steven, @Michael Enright would like to know how you arrived at the formula
r a r b + r b r c + r c r a = s 2
Log in to reply
@Calvin Lin @Michael Enright : Here it is.
 Upgrade to IE 1 to view this content.
Upgrade to IE 1 to view this content.
First, we will prove that
[ A B C ] = r a ( s − a ) ,
where [ A B C ] is the area of A B C , r a is the radius of the A-excircle, and s is the semiperimeter. (Skip to the black square if you want to get to the main proof.)
Let X be the tangent point of the A-excircle with B C , as shown above. Also, let B 1 be the tangent to A B and C 1 be the tangent to A C .
We will find the area of A B C as the area of right triangles A B 1 I A and A C 1 I A minus the area of B 1 B C C 1 I A .
First, B X = s − c and C X = s − b , as shown in this wiki . Because tangents from a point to a circle are equal, we also have B B 1 = s − c and C C 1 = s − b . Thus, A B 1 = s = A C 1 and
[ A B 1 I A ] + [ A C 1 I A ] = 2 ( A B 1 ) ( B 1 I A ) + ( A C 1 ) ( C 1 I A ) = 2 s r a + s r a = s r a .
To find [ B 1 B C C 1 I A ] , we note that △ B X I A ≅ △ B B 1 I A and △ C X I A ≅ △ C C 1 I A . So,
[ B 1 B C C 1 I A ] = [ B X I A ] + [ B B 1 I A ] + [ C X I A ] + [ C C 1 I A ] = 2 ( [ B X I A ] + [ C X I A ] ) = 2 [ B C I A ] = a r a .
Finally,
[ A B C ] = [ A B 1 I A ] + [ A C 1 I A ] − [ B 1 B C C 1 I A ] = s r a − a r a = r a ( s − a ) ,
as desired. ■
We have r a = s − a [ A B C ] . Similarly, r b = s − b [ A B C ] and r c = s − c [ A B C ] . Also, [ A B C ] = s ( s − a ) ( s − b ) ( s − c ) .
Thus, we have
r a r b + r b r c + r c r a = ( s − a ) ( s − b ) [ A B C ] 2 + ( s − b ) ( s − c ) [ A B C ] 2 + ( s − c ) ( s − a ) [ A B C ] 2 = ( s − a ) ( s − b ) ( s − c ) ( ( s − c ) + ( s − a ) + ( s − b ) ) [ A B C ] 2 = ( s − a ) ( s − b ) ( s − c ) ( 3 s − 2 s ) ( s ( s − a ) ( s − b ) ( s − c ) ) = s 2 .
Did the same way.
It is clear that the circles described in the problem are the excircles of A B C . Let r a , r b , and r c be the radii of these excircles. It can be proven that
r a r b + r b r c + r c r a = s 2 ,
where s represents the semiperimeter of A B C . Plugging our radii lengths in, we get
s 2 s 2 s 2 A B + B C + C A A B + B C + C A = 3 ( 4 ) + 4 ( 5 ) + 5 ( 3 ) = 4 7 = 4 7 = 4 7 = 2 4 7 .
Thus, p = 2 , q = 4 7 , and p + q = 4 9 .