Three Lines, Three Circles v2
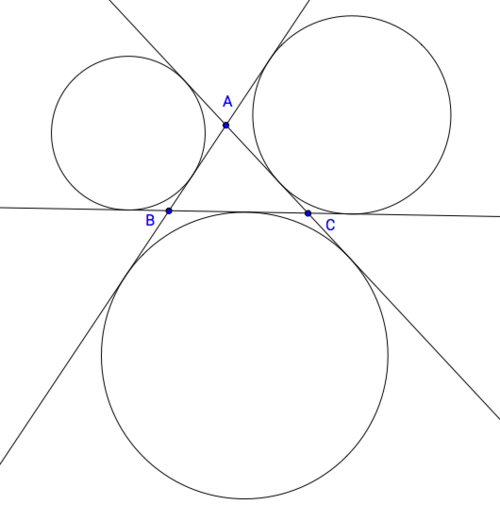 Lines
l
,
m
,
n
in the same plane are such that
l
∩
m
=
A
,
m
∩
n
=
B
,
l
∩
n
=
C
,
and
A
=
B
=
C
.
The three circles that are tangent to
l
,
m
,
and
n
but not in the interior of
A
B
C
have radii
3
,
4
,
and
5
.
If the area of
A
B
C
can be represented by
Lines
l
,
m
,
n
in the same plane are such that
l
∩
m
=
A
,
m
∩
n
=
B
,
l
∩
n
=
C
,
and
A
=
B
=
C
.
The three circles that are tangent to
l
,
m
,
and
n
but not in the interior of
A
B
C
have radii
3
,
4
,
and
5
.
If the area of
A
B
C
can be represented by
r p q ,
where p , q and r are positive integers such that p and r are relatively prime and q is not divisible by the square of any prime, find p + q + r .
Notes:
Assume that such a configuration described in the problem is possible.
a ∩ b means the intersection of lines a and b .
See the first problem here .
The answer is 154.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It is clear that the circles described in the problem are the excircles of A B C . Let r a , r b , and r c be the radii of these excircles. Also, let r be the inradius of A B C . It can be proven that
[ A B C ] = r r a r b r c ,
where [ A B C ] denotes the area of A B C . We already know the exradii lengths. To get the inradius, we use the fact that
r a 1 + r b 1 + r c 1 = r 1 .
From this, we get
r = r a 1 + r b 1 + r c 1 1 = 3 1 + 4 1 + 5 1 1 = 6 0 4 7 1 = 4 7 6 0
and
[ A B C ] = r r a r b r c = ( 4 7 6 0 ) ( 3 ) ( 4 ) ( 5 ) = 4 7 6 0 = 4 7 6 0 4 7 .
Thus, p = 6 0 , q = 4 7 , and r = 4 7 , and p + q + r = 1 5 4 .
Same solution.
same analysis, you post it well