Three Logs
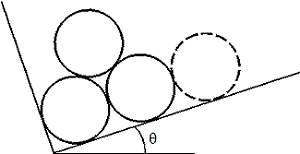
Smooth, identical logs are piled in a stake truck. The truck is forced off the highway and comes to rest on an even keel lengthwise but with the bed at an angle of with the horizontal.
As the truck is unloaded, the removal of the dotted log leaves the remaining three in a condition where they are just ready to slide. That is, if were any smaller, the logs would fall down.
Find such
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Substituting ( 2 ) in ( 1 ) and solving for θ , we obtain the desired result: θ = tan − 1 ( 3 3 1 ) ≈ 1 1 ∘