Three Magnetically Coupled Coils
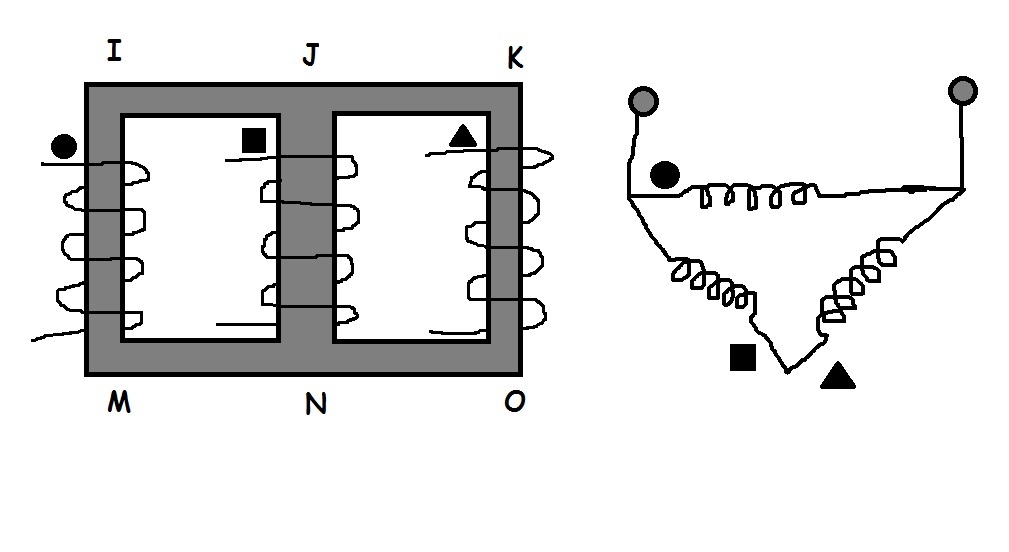
The frame shown on the left is made of material with magnetic permeability . The magnetic field in each segment of the frame is uniform and parallel to that segment. Coil circle has turns, coil square has turns, and coil triangle has turns, where is an even integer. The dimensions of each segment of the frame are listed in the table below, where :
| Segment | Length | Cross-sectional Area |
The coils are connected as shown on the right to form a single equivalent inductance. The equivalent inductance can be expressed as:
where and are coprime positive integers. Determine .
The answer is 203.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From Gauss' Law for Magnetic Fields, we have:
B N M A = B M I A
B M I A = B I J A
B N O A = B O K A
B O K A = B K J A
B I J A + B N J ( 2 A ) + B K J A = 0 [EQUATION 1]
Thus, we can let:
B 1 = B N M = B M I = B I J
B 2 = B N J
B 3 = B N O = B O K = B K J
Rewriting and simplifying [EQUATION 1], we get:
B 1 + 2 B 2 + B 3 = 0 [EQUATION 2]
Let I 1 be the current through coil circle that flows from the marked end to the unmarked end.
Let I 2 be the current through coil square that flows from the marked end to the unmarked end.
Let I 3 be the current through coil triangle that flows from the marked end to the unmarked end.
Applying Ampere's Law to loops N J I M and O K J N :
N I 2 − 2 N I 1 = μ B 2 4 L − μ B 1 9 L [EQUATION 3]
2 N I 3 − N I 2 = μ B 3 9 L − μ B 2 4 L [EQUATION 4]
From [EQUATION 2], [EQUATION 3], and [EQUATION 4], it can be shown that:
⎣ ⎡ B 1 B 2 B 3 ⎦ ⎤ = L μ N ⎣ ⎡ 1 1 7 2 2 − 1 3 1 − 1 1 7 4 − 1 3 1 1 3 1 − 1 3 1 − 1 1 7 1 − 5 2 1 2 3 4 1 1 ⎦ ⎤ ⎣ ⎡ I 1 I 2 I 3 ⎦ ⎤
Applying Faraday's Law to each coil:
V 1 = d t d ( 2 N B 1 A )
V 2 = d t d ( N B 2 ( 2 A ) )
V 3 = d t d ( 2 N B 3 A )
Thus, we get:
⎣ ⎡ V 1 V 2 V 3 ⎦ ⎤ = L μ N 2 A ⎣ ⎡ 1 1 7 4 4 − 1 3 2 − 1 1 7 2 − 1 3 2 1 3 2 − 2 6 1 − 1 1 7 2 − 2 6 1 4 6 8 1 1 ⎦ ⎤ d t d ⎣ ⎡ I 1 I 2 I 3 ⎦ ⎤ [EQUATIONS 5]
The equivalent inductance is defined as:
V t e r m i n a l = L e q d t d I t e r m i n a l [EQUATION 6]
From Kirchhoff's Loop Rule, we have:
V t e r m i n a l = V 1 = − V 2 + V 3 [EQUATION 7]
From Kirchhoff's Junction Rule, we have:
I t e r m i n a l = I 1 − I 2 = I 1 + I 3 [EQUATION 8]
I 2 = − I 3 [EQUATION 9]
Applying [EQUATIONS 5] on [EQUATION 7] and noting [EQUATION 9] to relate the currents yields:
d t d I 3 = 5 5 1 1 2 d t d I 1 = − d t d I 2 [EQUATION 10]
Applying [EQUATION 10] on [EQUATION 7] yields:
V t e r m i n a l = 5 5 3 6 L μ N 2 A d t d I 1 [EQUATION 11]
Applying [EQUATION 10] on [EQUATION 8] yields:
d t d I t e r m i n a l = 5 5 1 6 7 d t d I 1 [EQUATION 12]
Using [EQUATION 6], [EQUATION 11], and [EQUATION 12]:
L e q = 1 6 7 3 6 L μ N 2 A