Three mutually tangent circles in a triangle

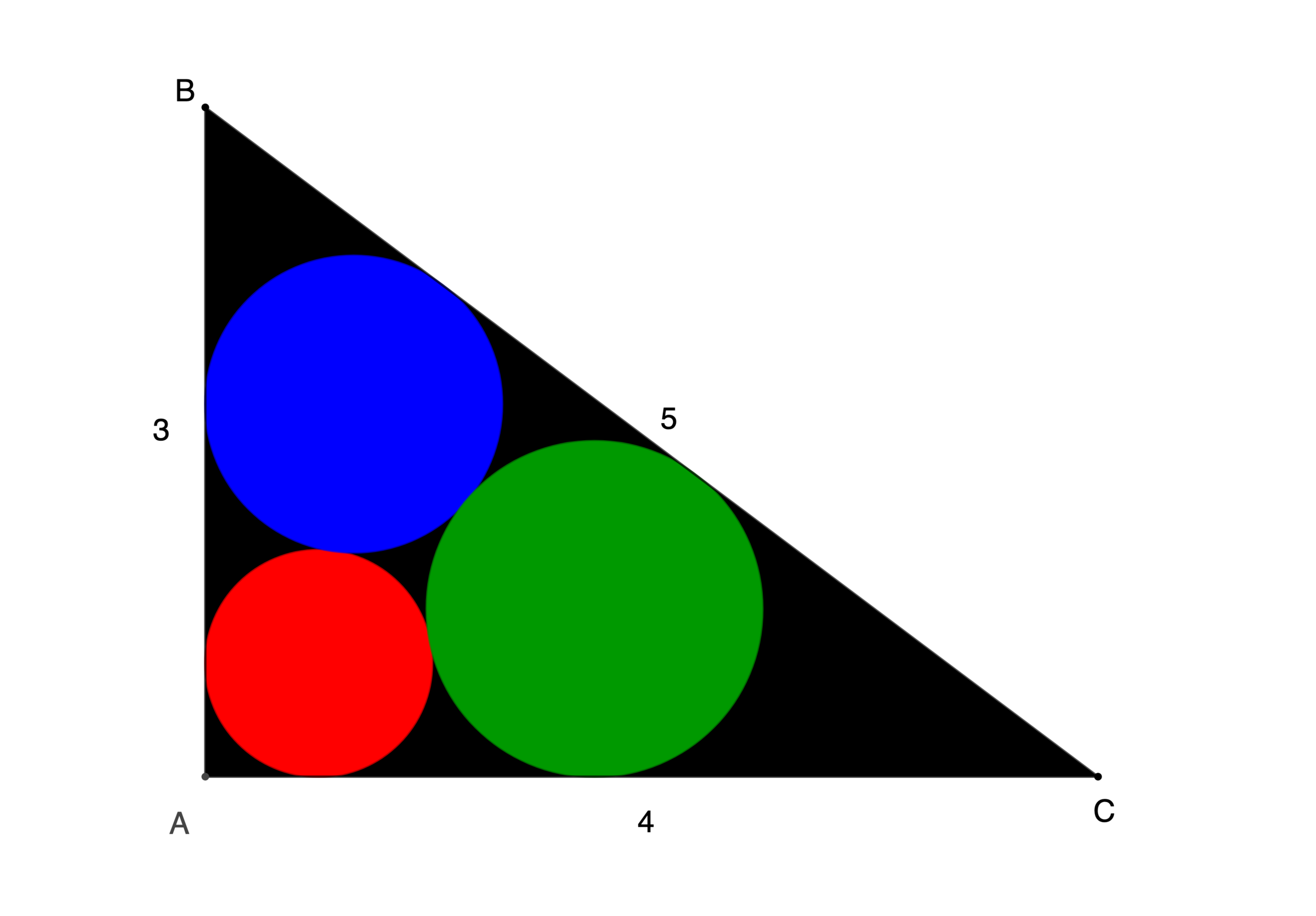
There is exactly one way to inscribe three mutually tangent circles in a triangle. Such circles are called Malfatti circles and have an interesting history. There are several formulae (which I won't prove) for calculating their radii, but perhaps the most convenient are described here . Call the three radii $r_a, r_b,$ and $r_c$ , and take $r_a$ as the red circle.

$r_a = \dfrac{ r(1+\tan \frac{B}{4}) (1+\tan \frac{C}{4}) }{2(1+\tan \frac{A}{4} )} , \enspace$ $r_b = \dfrac{ r(1+\tan \frac{A}{4}) (1+\tan \frac{C}{4}) }{2(1+\tan \frac{B}{4}) } , \enspace$ $r_c = \dfrac{ r(1+\tan \frac{A}{4}) (1+\tan \frac{B}{4}) }{2(1+\tan \frac{C}{4}) }$

Where $r$ is the inradius of $\triangle{ABC} = \dfrac{2\cdot\text{area}}{\text{perimeter}} = \dfrac{12}{12} = 1$

Let $A = \angle{CAB},\enspace B = \angle{ABC},\enspace C = \angle{BCA}$

$A = \frac{\pi}{2} \implies \tan (\frac{A}{4} )= \sqrt{2} - 1, \hspace{2mm} B = \cos^{-1}(\frac{4}{5})\implies \tan\frac{B}{4} = \sqrt{10} - 3, \hspace{2mm} C = \cos^{-1}(\frac{3}{5}) \implies \tan(\frac{C}{4}) = \sqrt{5} - 2$

Thus $r_a = \dfrac{(1+\sqrt{10}-3)(1+\sqrt{5}-2)}{2(1+\sqrt{2}-1)} = \dfrac{5 + \sqrt{2} - \sqrt{5} -\sqrt{10}}{2} \approx 0.5079$

So $\dfrac{a + \sqrt{b} - \sqrt{a} - \sqrt{c}}{b} \implies a=5, b=2, c=10, \text{and }a+b+c = \boxed{17}$

Let the radii of the red, blue, and green circles be $r_1$ , $r_2$ , and $r_3$ respectively. Then we note that for side $AB$ :

$\begin{aligned} r_1 + \sqrt{(r_2+r_1)^2 - (r_2-r_1)^2} + r_2 \blue{\cot \frac B2} & = AB & \small \blue{\text{Since }\tan \frac B2 = \frac 12} \\ \implies r_1 + 2\sqrt{r_1r_2} + 2r_2 & = 3 \end{aligned}$

We get similar equations for the other two sides and we have the three equations as follows:

$\begin{cases} \begin{aligned} r_1 + 2\sqrt{r_1r_2} + 2r_2 & = 3 & ...(1) \\ r_1 + 2\sqrt{r_3r_1} + 3r_3 & = 4 & ...(2) \\ 2r_2 + 2\sqrt{r_2r_3} + 3r_2 & = 5 & ...(3) \end{aligned} \end{cases}$

Solving the quadratic equation $(1)$ for $\sqrt{r_2}$ , we have $\sqrt{r_2} = \dfrac {\sqrt{6-r_1}-\sqrt{r_1}}2$ . Solving equation $(2)$ , $r_3 = \dfrac {\sqrt{12-2r_1}-\sqrt{r_1}}3$ .

From $(1)+(2)-(3)$ :

$\begin{aligned} r_1 + (\sqrt{r_2}+\sqrt{r_3})\sqrt{r_1} - \sqrt{r_2r_3} & = 1 \\ r_1 + \frac {(3+2\sqrt 2)\sqrt{r_1(6-r_1)}- 5r_1}6 - \frac {6\sqrt 2-(1+\sqrt 2)\sqrt{r_1(6-r_1)}+(1-\sqrt 2)r_1}6 & = 1 \\ \sqrt 2 r_1 + (4+3\sqrt 2)\sqrt{r_1(6-r_1)} - 6\sqrt 2 & = 6 \end{aligned}$

$\begin{aligned} \implies (4+3\sqrt 2)\sqrt{r_1(6-r_1)} & = 6(1+\sqrt 2) - \sqrt 2 r_1 \\ (34+24\sqrt 2)(6r_1 - r_1^2) & = 108 + 72\sqrt 2 - 12(\sqrt 2 + 2)r_1 + 2r_1^2 \\ (18+12 \sqrt 2)r_1^2 - 6(19+13\sqrt 2)r_1 + 54 + 36\sqrt 2 & = 0 \\ (3+2 \sqrt 2)r_1^2 - (19+13\sqrt 2)r_1 + 9 + 6\sqrt 2 & = 0 \\ r_1^2 - (5+\sqrt 2)r_1 + 3 & = 0 \end{aligned}$

$\begin{aligned} \implies r_1 & = \frac {5+\sqrt 2 - \sqrt{27+10\sqrt 2-12}}2 = \frac {5+\sqrt 2 - \sqrt{5(3+2\sqrt 2)}}2 \\ & = \frac {5+\sqrt 2 - \sqrt 5 - \sqrt{10}}2 \end{aligned}$

Therefore $a+b+c = 5+2+10 = \boxed{17}$

Let x be red, y be blue and z be green circle radius. Write the following

x+2√(xz)+z/[tan(C/2)]=4, tan(C)=3/4

x+2√(xy)+y/[tan(B/2)]=3, tan(B)=4/3

y/[tan(B/2)]+z/[tan(C/2)]+2√(yz)=5

Solve using WolframAlpha

x=(1/2)[5+√2−√5−√10]

Answer=17