Three pentagons
In the diagram below, we have 3 regular pentagons and 5 identical circles with the following properties:
- The 5 circles centered at A , B , C , D , E are tangent to one another, and pentagon A B C D E has area S ( 5 ) .
- K L , L M , M N , N O , O K are tangent to circles centered at A , B , C , D , E respectively, and pentagon K L M N O has area S M ( 5 ) .
- R Q , Q P , P T , T S , S R are tangent to circles centered at A , B , C , D , E respectively, and pentagon P Q R S T has area S m ( 5 ) .
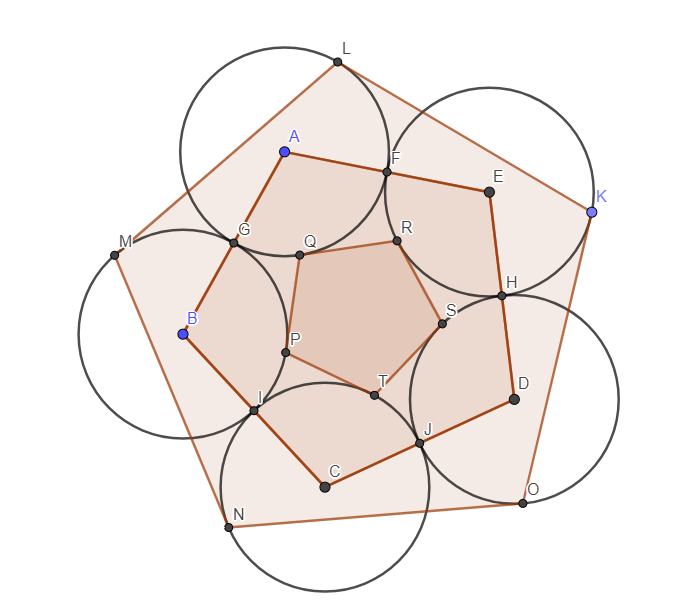
Find the expression S ( 5 ) S M ( 5 ) + S m ( 5 ) = Z U + V W , where U , V , W , Z are coprime positive integers and W is square-free.
What is the value of U + V + W + Z ?
Note: The above problem can be considered as the regular n -gon equivalent of this problem with n = 5 .
Bonus: Generalize for a regular n -gon and find the limit n → ∞ lim S ( n ) S M ( n ) + S m ( n ) .
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Suppose that the original polygon has side 2 . Extend the lines A E and L K to meet at X . Then, using the right-angled triangle A L X and using the Sine Rule in the triangle K E X , we deduce that A X = sec θ and E X = cos α sec θ , and hence 2 = ( 1 − cos α ) sec θ , where α is the exterior angle of the polygon.
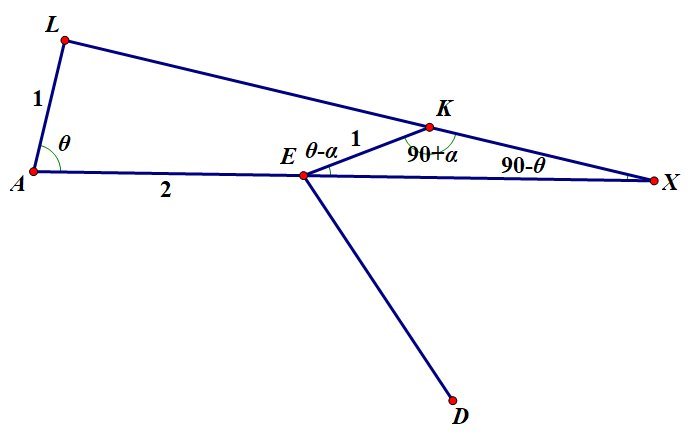
Similarly, L X = tan θ and K X = sin ( θ − α ) sec θ , and hence L K = tan θ − sin ( θ − α ) sec θ = ( 1 − cos α ) tan θ + sin α = ( 3 − cos α ) ( 1 + cos α ) + sin α A similar set of calculations shows that Q R = ( 3 − cos α ) ( 1 + cos α ) − sin α Thus S S M + S m = 4 L K 2 + Q R 2 = 2 1 [ ( 3 − cos α ) ( 1 + cos α ) + sin 2 α ] = 2 + cos α − cos 2 α This argument works for any regular polygon, and so S ( n ) S M ( n ) + S m ( n ) = 2 + cos n 2 π − cos 2 n 2 π for any integer n ≥ 5 . The argument can be adjusted to cope with n = 3 , 4 - in these cases θ < α . The formula for the fraction is the same, however. When n = 5 (this problem) we obtain the ratio 8 1 ( 1 1 + 3 5 ) , giving the answer 2 7 . In addition n → ∞ lim S ( n ) S M ( n ) + S m ( n ) = 2
A regular polygon with n sides of length s has interior angles of θ = π − n 2 π , an apothem of a = 2 tan n π s , a radius of R = 2 sin n π s , and area of A = 2 n R 2 sin n 2 π . Therefore, if r is the length of the radius of each circle, the regular polygon made from the centers of the circles have sides of s = 2 r and therefore an area of S ( n ) = 2 n R 2 sin n 2 π = 2 n ( 2 sin n π 2 r ) 2 sin n 2 π or S ( n ) = n r 2 cot n π
Let Z be the center of all the regular polygons. Then we can find the radius of the small regular polygon by examining △ A Q Z .
As the radius of one of the circles, A Q = r . As the radius of the regular polygon with sides 2 s , A Z = sin n π r . Finally, as the sum of a right angle (from the tangent line) and half the interior angle of the regular polygon, ∠ A Q Z = 2 π + 2 1 ( π − n 2 π ) = π − n π . Using the law of cosines, we have ( sin n π r ) 2 = r 2 + Q Z 2 − 2 r Q Z cos ( π − n π ) which after solving using the quadratic formula and simplifying means Q Z = − cos n π + cot n π sin 2 n π + 1 . Since Q Z is the radius of the small regular polygon, its area is S m ( n ) = 2 n R 2 sin n 2 π = 2 n ( − cos n π + cot n π sin 2 n π + 1 ) 2 sin n 2 π or S m ( n ) = n r 2 cot 2 π ( cos 2 n π ( 3 − 2 cos 2 n π ) − 2 cos 2 n π sin n π sin 2 n π + 1 )
We can find the radius of the large regular polygon by examining △ A L Z .
As the radius of one of the circles, A L = r . As from before, A Z = sin n π r . Finally, ∠ A L Z is the interior angle of the large regular polygon minus half the interior angle of the large regular polygon ( ∠ K L Z ) minus the difference of the interior angle of the large regular polygon and a right angle from the tangent line ( ∠ A L M = ∠ K L M − ∠ K L A ), which means ∠ A L Z = ( π − n 2 π ) − 2 1 ( π − n 2 π ) − ( ( π − n 2 π ) − 2 π ) = n π . Using the law of cosines, we have ( sin n π r ) 2 = r 2 + L Z 2 − 2 r L Z cos ( n π ) which after solving using the quadratic formula and simplifying means L Z = cos n π + cot n π sin 2 n π + 1 . Since L Z is the radius of the large regular polygon, its area is S M ( n ) = 2 n R 2 sin n 2 π = 2 n ( cos n π + cot n π sin 2 n π + 1 ) 2 sin n 2 π or S M ( n ) = n r 2 cot 2 π ( cos 2 n π ( 3 − 2 cos 2 n π ) + 2 cos 2 n π sin n π sin 2 n π + 1 )
Therefore, the ratio S ( n ) S M ( n ) + S m ( n ) = 2 cos 2 n π ( 3 − 2 cos 2 n π )
Since lim n → ∞ cos n π = 1 , n → ∞ lim S ( n ) S M ( n ) + S m ( n ) = 2 ⋅ 1 2 ( 3 − 2 ⋅ 1 2 ) = 2 .
When n = 5 , cos 5 π = 4 1 + 5 , and the ratio is 2 ( 4 1 + 5 ) 2 ( 3 − 2 ( 4 1 + 5 ) 2 ) = 8 1 1 + 3 5 , so U = 1 1 , V = 3 , W = 5 , and Z = 8 , and U + V + W + Z = 2 7 .