Three-phase induction motor

Electricity and Magnetism Level 4

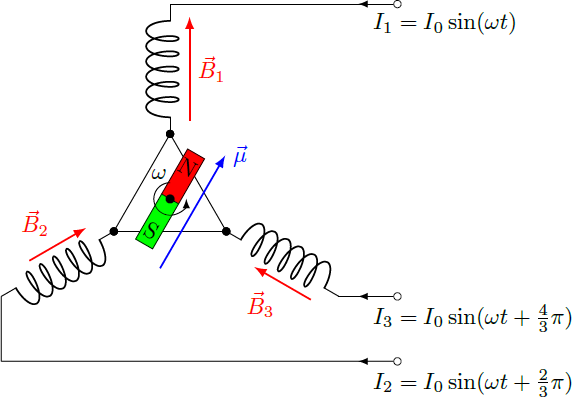
In an induction motor three coils are arranged symmetrically about a permanent magnet, which is rotatably mounted. The coils are operated with a three-phase alternating current, so that the currents have a phase difference of $120^\circ$ relative to each other. At the location of the permanent magnet, the $k$ -th coil generates a magnetic field $\vec B_k (t) = B_0 \sin (\omega t + \phi_k) \vec e_k, \quad k = 1,2,3$ with an amplitude $B_0 = 20 \, \text{mT}$ . The unit vectors $\vec e_k$ are parallel to the corresponding coil axis and have an angle of $120^\circ$ relative to each other. The permanent magnet with the magnetic moment $\mu = 1000 \, \text{Nm} / \text{T}$ is set in uniform rotation by the magnetic field.

What is the maximum torque $T_\text{max}$ , that the three-phase induction motor can produce?

T_\text{max} = 60 \,\text{Nm}

T_\text{max} = 10 \,\text{Nm}

T_\text{max} = 30 \,\text{Nm}

T_\text{max} = 40 \,\text{Nm}

T_\text{max} = 20 \,\text{Nm}

T_\text{max} = 50 \,\text{Nm}

1 solution

Markus Michelmann
May 8, 2018

The unit vectors of the coil directions are $\begin{aligned} \vec e_k &= \left(\begin{array}{c} - \sin( \phi_k ) \\ \cos( \phi_k ) \end{array} \right)= \left(\begin{array}{c} - \sin( \frac{2}{3} \pi (k-1) ) \\ \cos( \frac{2}{3} \pi (k-1) ) \end{array} \right), \quad k = 1,2,3 \\ &= \left(\begin{array}{c} 0 \\ 1 \end{array} \right), \quad \left(\begin{array}{c} -^{\sqrt{3}}\!/_2 \\ -^1\!/_2 \end{array} \right), \quad \left(\begin{array}{c} ^{\sqrt{3}}\!/_2 \\ -^1\!/_2 \end{array} \right) \end{aligned}$ where the angle $\phi_k = \frac{2}{3} \pi (k-1)$ corresponds also to the phase angle of the currents $I_k = I_0 \sin(\omega t + \phi_k)$ . The total magnetic field is calculated via a vector sum: $\begin{aligned} \vec B(t) &= \sum_{k = 1}^3 \vec B_k(t) \\ &= \sum_{k = 1}^3 B_0 \sin(\omega t + \phi_k) \vec e_k \\ &= \sum_{k = 1}^3 B_0 [\sin(\omega t) \cos(\phi_k) + \cos(\omega t) \sin(\phi_k)] \left(\begin{array}{c} - \sin( \phi_k ) \\ \cos( \phi_k ) \end{array} \right) \\ &= B_0 \sin(\omega t) \left(\begin{array}{c} - \sum_{k = 1}^3 \cos(\phi_k) \sin( \phi_k ) \\ \sum_{k = 1}^3 \cos^2( \phi_k ) \end{array} \right) + B_0 \cos(\omega t) \left(\begin{array}{c} - \sum_{k = 1}^3 \sin^2(\phi_k) \\ \sum_{k = 1}^3 \sin(\phi_k)\cos( \phi_k ) \end{array} \right)\\ &= B_0 \sin(\omega t) \left(\begin{array}{c} 0 \\ \frac{3}{2} \end{array} \right) + B_0 \cos(\omega t) \left(\begin{array}{c} \frac{3}{2} \\ 0 \end{array} \right) \\ &= \frac{3}{2} B_0 \left(\begin{array}{c} \cos(\omega t) \\ \sin(\omega t) \end{array} \right) \end{aligned}$ In line three, we used the addition theorem of sine. The total magnetic field $\vec B$ has an amplitude of $|\vec B| = \frac {3} {2} B_0$ and makes a circular motion with the frequency $\omega$ of the alternating current. At idle, the magnet simply follows the circular motion of the magnetic field, so that $\vec \mu \parallel \vec B$ . Under load, both vectors point in different directions with an angle $\alpha = \angle (\vec B, \vec \mu)$ between the two. The torque exerted by the engine results $T = |\vec \mu \times \vec B| = \frac{3}{2} \mu B_0 \sin(\alpha)$ A right angle $\alpha = 90^\circ$ results in a maximal torque $T_\text{max} = \frac{3}{2} \mu B_0 = \frac{3}{2} \cdot 1000 \cdot 2\cdot 10^{-2} \,\mathrm{Nm} = 30 \,\mathrm{Nm}$

Three-phase induction motor

1 solution

0 pending reports