Three-Phase Transmission Line

Electricity and Magnetism Level pending

An unbalanced three-phase voltage source feeds a balanced set of load resistors through a transmission line. The three phases of the transmission line are magnetically coupled, which can be modeled using self and mutual impedances as follows:

V A S − Z S I A − Z M I B − Z M I C = V A R V B S − Z M I A − Z S I B − Z M I C = V B R V C S − Z M I A − Z M I B − Z S I C = V C R V_{AS} - Z_S I_A - Z_M I_B - Z_M I_C = V_{AR} \\ V_{BS} - Z_M I_A - Z_S I_B - Z_M I_C = V_{BR} \\ V_{CS} - Z_M I_A - Z_M I_B - Z_S I_C = V_{CR}

In the circuit, the star (neutral) point of the voltage sources is taken as the voltage reference. By convention, the currents flow across the transmission line from left to right. The system parameters are:

V A S = 70 e j 0 V B S = 100 e − j 2 π / 3 V C S = 120 e j 2 π / 3 Z S = 1 + j 10 Z M = 1 + j 5 R = 10 R N = 2 V_{AS} = 70 \, e^{j 0} \\ V_{BS} = 100 \, e^{-j 2 \pi/3} \\ V_{CS} = 120 \, e^{j 2 \pi/3} \\ Z_S = 1 + j 10 \\ Z_M = 1 + j 5 \\ R = 10 \\ R_N = 2

What is the magnitude of the current flowing in phase A A of the transmission line?


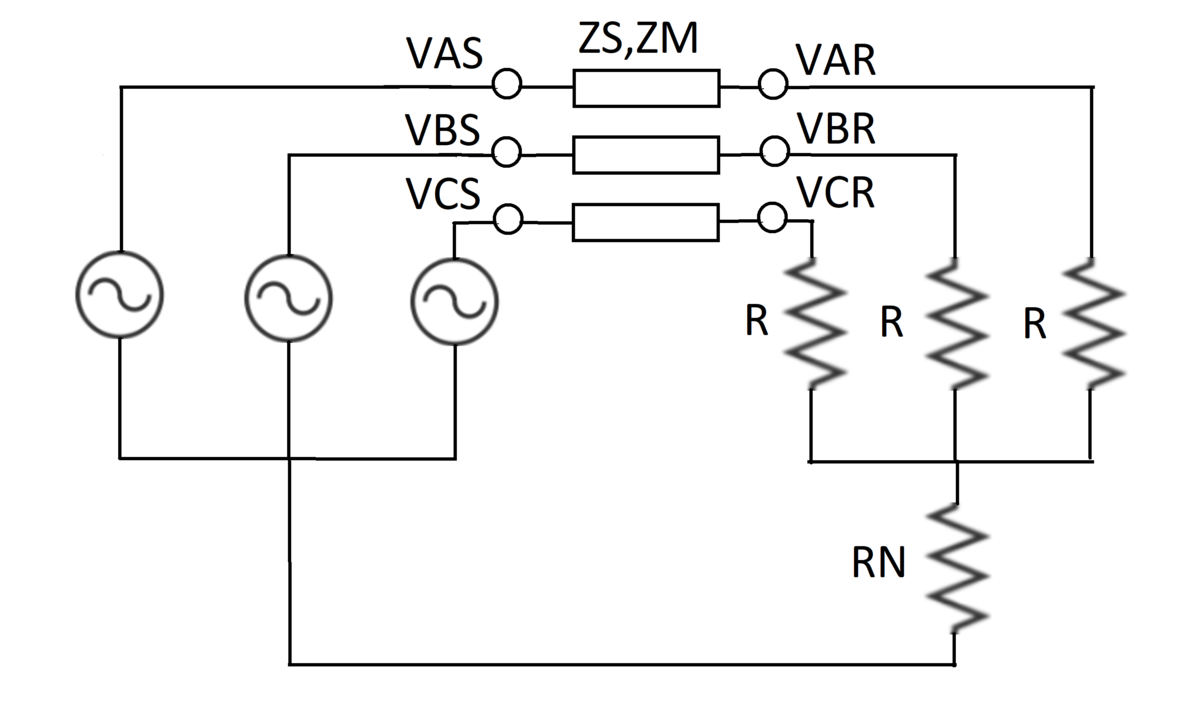
The answer is 7.07.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Karan Chatrath
Oct 31, 2019

The first step is writing down the circuit equations by applying Kirchoff's laws.

V A S = ( V A S − V A R ) + I A R + ( I A + I B + I C ) R N V_{AS} = (V_{AS} - V_{AR}) + I_AR + (I_A + I_B + I_C)R_N V B S = ( V B S − V B R ) + I B R + ( I A + I B + I C ) R N V_{BS} = (V_{BS} - V_{BR}) + I_BR + (I_A + I_B + I_C)R_N V C S = ( V C S − V C R ) + I C R + ( I A + I B + I C ) R N V_{CS} = (V_{CS} - V_{CR}) + I_CR + (I_A + I_B + I_C)R_N

Replacing the equation V A S − V A R V_{AS} - V_{AR} by the given transmission line model, in each equation, re-writing and simplifying gives:

[ V A S V B S V C S ] = [ D N N N D N N N D ] [ I A I B I C ] ⟹ V = Z I \left[\begin{matrix} V_{AS} \\V_{BS} \\V_{CS} \end{matrix}\right] = \left[\begin{matrix} D&N&N\\N&D&N\\N&N&D \end{matrix}\right] \left[\begin{matrix} I_{A} \\I_{B} \\I_{C} \end{matrix}\right] \implies V = ZI

Where:

N = Z M + R N N = Z_M + R_N D = Z S + R N + R D = Z_S + R_N+R

Let, Z Z be referred to as an 'impedance matrix'. From here, the currents can be computed by:

I = Z − 1 V \boxed{I = Z^{-1}V}

The above computation is done using a computer to save time.

Finally, the first element of the column matrix I I is extracted and its modulus is computed which is the answer. The current magnitude I A ≈ 7.072 \boxed{I_A \approx 7.072}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

With my limited exposure to electrical circuits, I have never come across such a model describing transmission lines. Apart from this steady-state analysis, It would be interesting to see how the behaviour of the circuit evolves with time (with the inclusion of other electrical elements -inductors etc. that make up the impedances).

Karan Chatrath - 1 year, 7 months ago

Log in to reply

This is a typical representation for an overhead 3-phase transmission line. Indeed, we could make a time-domain version of this. That's a fun exercise. In that case, there are three resistive drop terms and three inductive drop terms for each phase of the T-line.

Steven Chase - 1 year, 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...