Three-Phase with Floating Neutrals

Electricity and Magnetism Level 5

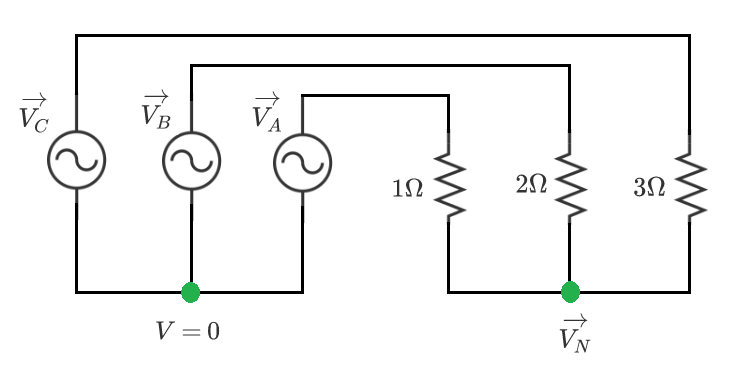
A three-phase AC circuit contains three ideal sinusoidal voltage sources and a load consisting of three resistors. The voltage sources share a common neutral, and the resistors share a common neutral. The two neutrals are floating, and are not directly connected to each other.

The voltage sources have values ( V A ⃗ , V B ⃗ , V C ⃗ ) = ( 1 ∠ 0 ∘ , 1 ∠ − 120 ∘ , 1 ∠ 12 0 ∘ ) (\vec{V_A},\vec{V_B},\vec{V_C}) = (1\angle0 ^\circ, \, 1\angle{-120} ^\circ, 1\angle120 ^\circ) . The resistor values are shown in the diagram.

Consider the source neutral to be the voltage reference for the circuit ( V = 0 ) (V = 0) . Let V N ⃗ \vec{V_N} be the voltage at the load neutral with respect to the source neutral.

What is the magnitude of V N ⃗ \vec{V_N} , to 3 decimal places?

Note: All voltage magnitudes are given in RMS, and the answer is expected in the same format. The symbol " ∠ \angle " indicates the complex phase angle of a sinusoid.

Hint: The answer can be found by writing and solving one complex equation, equivalent to two real-valued equations.


The answer is 0.328.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chew-Seong Cheong
Mar 16, 2017

Similar solution with Steven Chase 's

Consider the current sum of the common neutral of the load and using Ohm's law for the currents.

V A ⃗ − V N ⃗ 1 + V B ⃗ − V N ⃗ 2 + V C ⃗ − V N ⃗ 3 = 0 V A ⃗ + 1 2 V B ⃗ + 1 3 V C ⃗ = ( 1 + 1 2 + 1 3 ) V N ⃗ 1 ∠ 0 ∘ + 1 2 ∠ − 12 0 ∘ + 1 3 ∠ 12 0 ∘ = 11 6 V N ∠ θ 1 + 1 2 ( − 1 2 − 3 2 i ) + 1 3 ( − 1 2 + 3 2 i ) = 11 6 V N ∠ θ 7 12 − 3 12 i = 11 6 V N ∠ θ 7 − 3 i = 22 V N ∠ θ ⟹ V N ∠ θ = 7 − 3 i 22 = 13 11 ∠ − tan ⁡ − 1 3 7 ⟹ V N ≈ 0.328 \begin{aligned} \frac {\vec{V_A}-\vec{V_N}}1 + \frac {\vec{V_B}-\vec{V_N}}2 + \frac {\vec{V_C}-\vec{V_N}}3 & = 0 \\ \vec{V_A} + \frac 12 \vec{V_B} + \frac 13 \vec{V_C} & = \left(1+\frac 12+\frac 13\right) \vec{V_N} \\ 1\angle 0^\circ + \frac 12 \angle -120^\circ + \frac 13 \angle 120^\circ & = \frac {11}6 V_N \angle \theta \\ 1 + \frac 12 \left(-\frac 12 - \frac {\sqrt 3}2i \right) + \frac 13 \left(-\frac 12 + \frac {\sqrt 3}2i \right) & = \frac {11}6 V_N \angle \theta \\ \frac 7{12} - \frac {\sqrt 3}{12}i & = \frac {11}6 V_N \angle \theta \\ 7 - \sqrt 3 i & = 22 V_N \angle \theta \\ \implies V_N \angle \theta & = \frac {7 - \sqrt 3i}{22} \\ & = \frac {\sqrt{13}}{11} \angle - \tan^{-1} \frac {\sqrt 3}7 \\ \implies V_N & \approx \boxed{0.328} \end{aligned}

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Steven Chase
Mar 16, 2017

The currents through the three resistors must sum to zero at the neutral. These currents can be calculated using Ohm's Law as follows:

V N ⃗ − V A ⃗ 1 + V N ⃗ − V B ⃗ 2 + V N ⃗ − V C ⃗ 3 = 0 V N ⃗ ( 1 + 1 2 + 1 3 ) = V A ⃗ + V B ⃗ 2 + V C ⃗ 3 \large{\frac{\vec{V_N} - \vec{V_A}}{1} + \frac{\vec{V_N} - \vec{V_B}}{2} + \frac{\vec{V_N} - \vec{V_C}}{3} = 0 \\ \vec{V_N}(1 + \frac{1}{2} + \frac{1}{3}) = \vec{V_A} + \frac{\vec{V_B}}{2} + \frac{\vec{V_C}}{3}}

Plugging in numbers gives V N ⃗ ≈ 0.328 ∠ − 13. 9 ∘ \vec{V_N} \approx 0.328\angle -13.9^\circ .

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...