Three Points
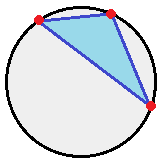
Three points are chosen randomly, uniformly, and independently on the circumference of a circle.
If there is a probability that the triangle formed by the three points has an obtuse angle that is greater or equal to , what is (in degrees)?
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let A , B , and C be the points on the circle and let O be the center of the circle. Then without loss of generality, the points can be rotated so that A is on the positive x -axis. Then let x be the central angle between A and B and y be the central angle between A and C . Then both x and y are such that 0 ≤ x < 3 6 0 ° and 0 ≤ y < 3 6 0 ° .
△ A O B , △ B O C , and △ A O C are isosceles triangles because each have two sides that are radii of the circle.
If y > x , the base angles of these triangles are 9 0 ° − 2 x , 9 0 ° − 2 y + 2 x , and 9 0 ° − 2 y , which makes ∠ B A C = 2 y − x , ∠ A B C = 1 8 0 ° − 2 y , and ∠ A C B = 2 x . For any one of these angles to be greater or equal to an obtuse angle α , either 2 y − x ≥ α or y ≥ x + 2 α , 1 8 0 ° − 2 y ≥ α or y ≤ 3 6 0 ° − 2 α , or 2 x ≥ α or x ≥ 2 α , which is shaded in green in the graph below:
By symmetry, if x > y , for any one of these angles to be greater or equal to an obtuse angle α , either y ≤ x − 2 α , x ≤ 3 6 0 ° − 2 α , or y ≥ 2 α , which is shaded in green in the graph below:
Combining these graphs gives a visual representation of all the possible triangles that can be made by three points on the circumference of a circle, with the green regions showing the triangles that have at least one angle that is greater or equal to an obtuse angle α :
The green regions have a combined area A G equivalent to 3 squares with sides of 3 6 0 ° − 2 α , so A G = 3 ( 3 6 0 ° − 2 α ) 2 , and the total area A T is a square with sides of 3 6 0 ° , so A T = 3 6 0 ° 2 . The probability P of the triangle having an obtuse angle that is greater or equal to α is therefore P = A T A G = 3 6 0 ° 2 3 ( 3 6 0 ° − 2 α ) 2 or P = 1 8 0 ° 2 3 ( 1 8 0 ° − α ) 2 , and when P = 1 2 1 , this solves to α = 1 5 0 ° .