Three roots in equation
Let K , L , and M be the roots of the equation 4 x 3 + 5 x 2 − 9 x + 1 2 = 0 .
Find K 8 + L 8 + M 8 .
The answer is 1939.3330.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The problem can be solved using Newton's sums method. Since the roots of 4 x 3 + 5 x 2 − 9 x + 1 2 = 0 are K , L , M , and d . Then by Vieta's formula , S 1 = K + L + M = − 4 5 , S 2 = K L + L M + M K = − 4 9 , S 3 = K L M = − 3 . Let P n = K n + L n + M n , where n is a positive integer and we need to find P 8 . Then we have:
P 1 = S 1 P 2 = S 1 P 1 − 2 S 2 P 3 = S 1 P 2 − S 2 P 1 + 3 S 3 P 4 = S 1 P 3 − S 2 P 2 + S 3 P 1 P 5 = S 1 P 4 − S 2 P 3 + S 3 P 2 P 6 = S 1 P 5 − S 2 P 4 + S 3 P 3 P 7 = S 1 P 6 − S 2 P 5 + S 3 P 4 P 8 = S 1 P 7 − S 2 P 6 + S 3 P 5 = − 4 5 = 1 6 9 7 = − 6 4 1 2 4 1 = 2 5 6 1 0 6 5 7 = − 1 0 2 4 1 1 6 5 8 5 = 4 0 9 6 1 2 0 4 8 4 9 = − 1 6 3 8 4 1 2 2 6 7 4 4 9 = 6 5 5 3 6 1 2 7 0 9 6 1 2 9
Therefore P 8 = 6 5 5 3 6 1 2 7 0 9 6 1 2 9 ≈ 1 9 3 9 . 3 3 3 . We can do the computation easily with an Excel spreadsheet.
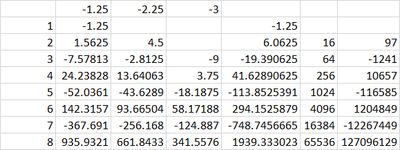
First solving it for general.
K + L + M = α
K L + L M + K M = β
K L M = γ
( K + L + M ) 2 = K 2 + L 2 + M 2 + 2 ( K L + L M + K M )
⇒ K 2 + L 2 + M 2 = α 2 − 2 β ( = α 1 )
( K L + L M + K M ) 2 = K 2 L 2 + L 2 M 2 + K 2 M 2 + 2 K L M ( K + L + M )
⇒ K 2 L 2 + L 2 M 2 + K 2 M 2 = β 2 − 2 α γ ( = β 1 )
K 2 L 2 M 2 = ( K L M ) 2 = γ 2 ( = γ 1 )
So, now we have
K 2 + L 2 + M 2 = α 1
K 2 L 2 + L 2 M 2 + K 2 M 2 = β 1
K 2 L 2 M 2 = γ 1
Doing the same thing again and again we can get
K 2 n + L 2 n + M 2 n for any n ≥ 0 , n ∈ Z
Taking α = 4 − 9
β = 4 − 5
γ = − 3
Doing the same procedure for 3 times we can get
K 8 + L 8 + M 8 = 2 5 6 2 1 2 7 0 9 6 1 2 9 ≈ 1 9 3 9 . 3 3 3