Three Square Problem
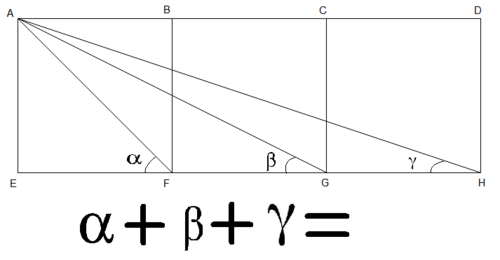 In the image above, have 3 squares
A
B
E
F
,
D
C
F
G
and
C
D
G
H
. Find the sum of the angles
α
,
β
and
γ
. Put you answer in degree.
In the image above, have 3 squares
A
B
E
F
,
D
C
F
G
and
C
D
G
H
. Find the sum of the angles
α
,
β
and
γ
. Put you answer in degree.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
great; love numberphile
F G A F = 2
A G A H = 5 1 0 = 2
A F F H = 2 2 = 2
△ A F H is similar to △ A F H then F A G = γ
β = G A C
α = F A E
α + β + γ = F A E + G A C + F A G = 9 0
∠ AGH = 45 (DIAGONALS BISECT THE ANGLES = 90/2).....
tan ∠ AFH= 1/2.....
tan ∠ AEH=1/3......
tan[ ∠ AFH+ ∠ AEH]= tan ∠ AFH+tan ∠ AEH/1-tan ∠ AFH tan ∠ AEH} = 1 − 1 / 2 ∗ 1 / 3 1 / 2 + 1 / 3 = 5 / 6 5 / 6 = 1........
So ∠ AFH+ ∠ AEH=45........
SO ∠ AGH+ ∠ AFH+ ∠ AEH = 45 + 45 = 9 0
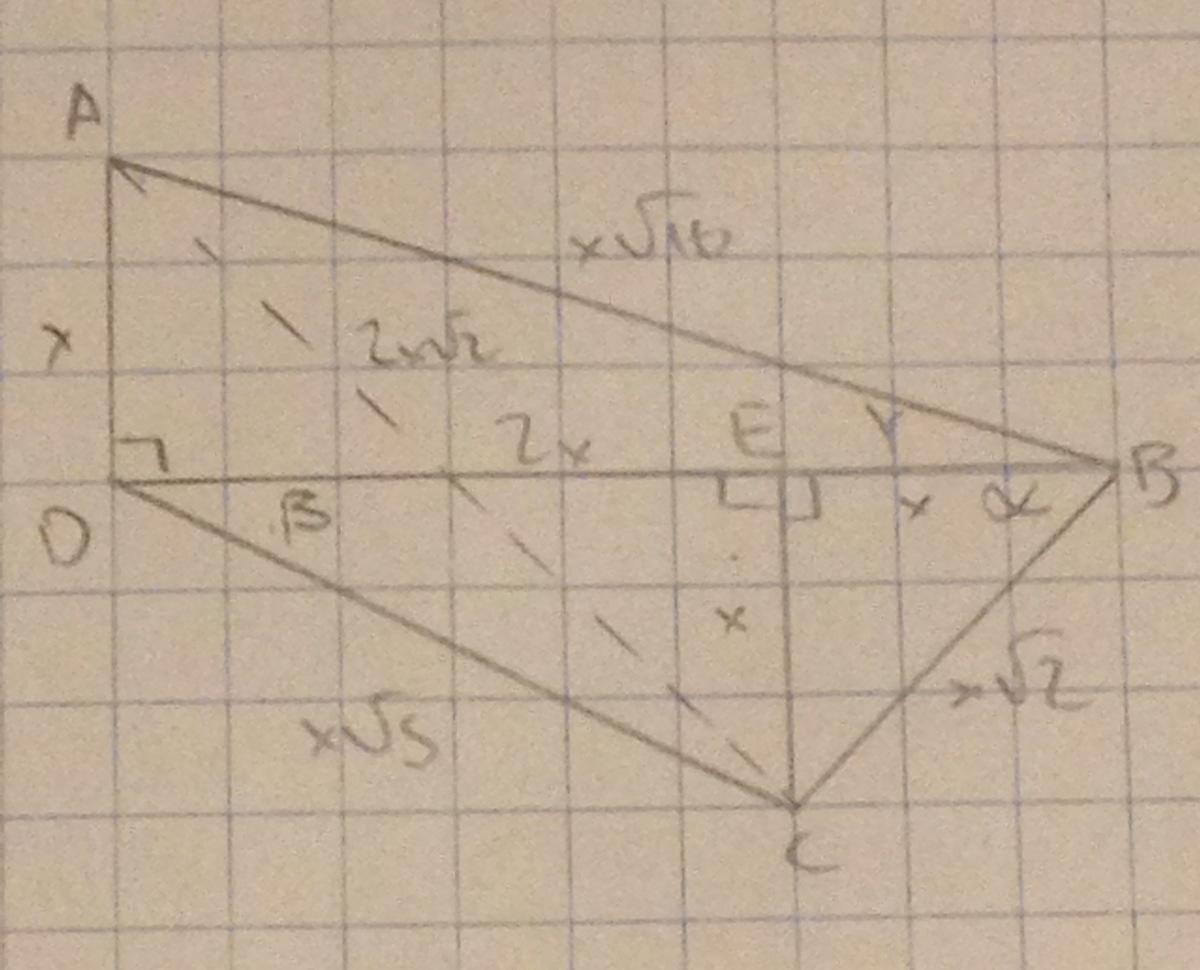 Rearrange the triangles as shown. If we let the original square have a side length of
x
, we can get the lengths shown by given measurements, the Pythagorean Theorem, or the Distance Formula. Note that the quadrilateral satisfies the converse of Ptolemy's Theorem. Therefore, this quadrilateral is a cyclic quadrilateral, so the opposite angles add to
1
8
0
∘
. This gives
α
+
β
+
γ
+
9
0
∘
=
1
8
0
∘
α
+
β
+
γ
=
9
0
∘
.
Rearrange the triangles as shown. If we let the original square have a side length of
x
, we can get the lengths shown by given measurements, the Pythagorean Theorem, or the Distance Formula. Note that the quadrilateral satisfies the converse of Ptolemy's Theorem. Therefore, this quadrilateral is a cyclic quadrilateral, so the opposite angles add to
1
8
0
∘
. This gives
α
+
β
+
γ
+
9
0
∘
=
1
8
0
∘
α
+
β
+
γ
=
9
0
∘
.
Alpha=45 ......angle made by diagonal Tan(beta)=1/2 Tan (gamma)=1/3 Now use property, tan (A+B)=(tanA+tanB) /1-tanAtanB Get the answer
Type on YouTube "The Three Square Geometry Problem - Numberphile"