Three Squares in Two Parallel Lines
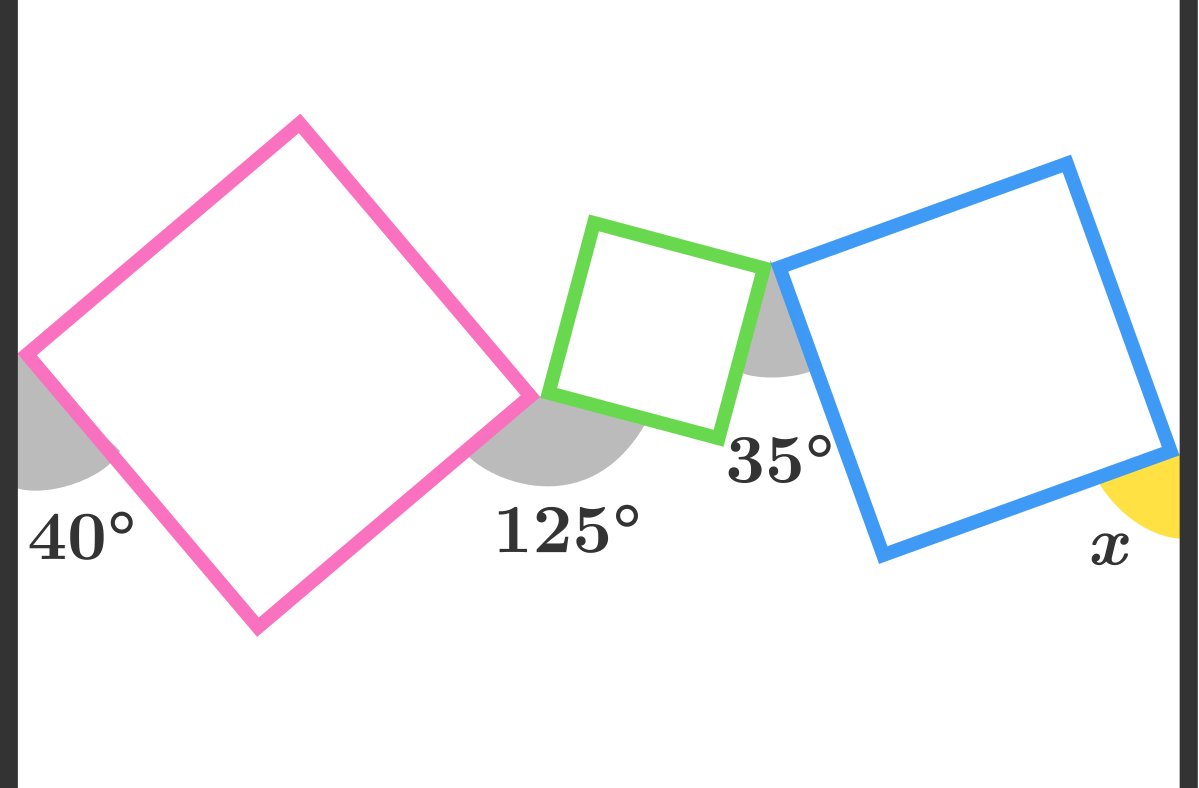
As shown in the diagram above, there lie 3 squares between 2 parallel lines such that each pair--(line, square) or (square, square)--just meet at a vertex. Find the measure of angle x in degrees.
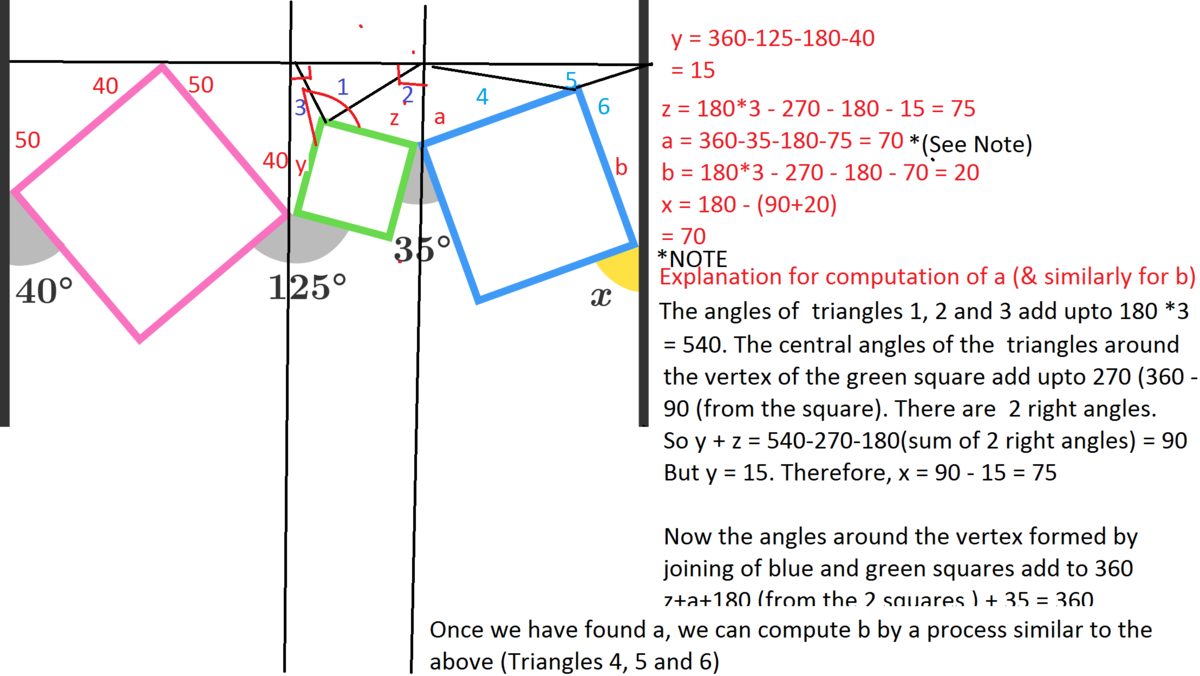
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
I don't really know geometry but I still go the answer doing something else. It was a bit like bearings. I said the parallel lines had bearing zero and could ten calculate the bearing of each line in every square in succession moving from right to left. Is that also ok? I down know this subtended rule thing :)
Log in to reply
Yes, that's a possible approach. Like in the above image, working out that the other angle between the vertical and the pink square is equal to 5 0 ∘ .
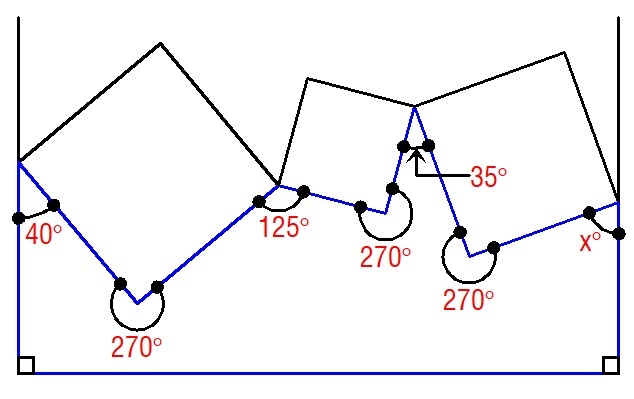 Draw a straight line perpendicular to the two parallel lines to have a nine-sided polygon. The sum of the interior angles of a nine sided polygon is
s
=
1
8
0
(
n
−
2
)
=
1
8
0
(
9
−
7
)
=
1
2
6
0
∘
. Considering my diagram,
x
=
1
2
6
0
−
4
0
−
2
7
0
−
1
2
5
−
2
7
0
−
3
5
−
2
7
0
−
9
0
−
9
0
=
7
0
∘
Draw a straight line perpendicular to the two parallel lines to have a nine-sided polygon. The sum of the interior angles of a nine sided polygon is
s
=
1
8
0
(
n
−
2
)
=
1
8
0
(
9
−
7
)
=
1
2
6
0
∘
. Considering my diagram,
x
=
1
2
6
0
−
4
0
−
2
7
0
−
1
2
5
−
2
7
0
−
3
5
−
2
7
0
−
9
0
−
9
0
=
7
0
∘
This is the best solution so far.
No where can I find that this formula works for concave polygons. Is this really ok?
nice answer, it makes me want to learn more.
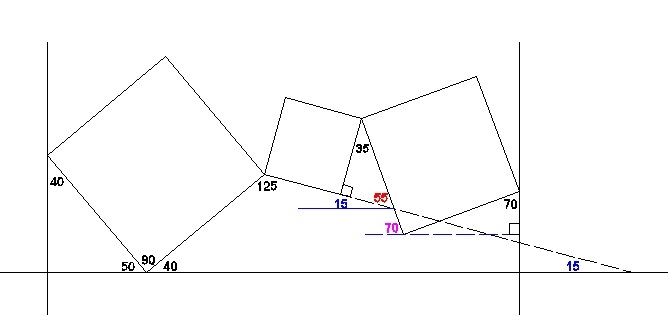 This is the conventional approach. I started from 40 degrees until I reached 70 degrees.
This is the conventional approach. I started from 40 degrees until I reached 70 degrees.
40 through 70 solutions
Connect the two parallel lines with prependicular line (under the squares) , then the shape constructed is a nonagon which have sum of internal angles of a nonagon = (9-2) x 180 = x + 270 +35 +270 + 125 + 270 + 40 + 90 + 90 , x = 70
all the opposite angles must add up to the same value for the 2 lines to be parallel
so 40+125+35+x must be equal to the sum of their complementary angles opposite angles are (left to right): 50, 55, 145 and 180-90-x
so 200+x=340-x
2x = 140
x+70
Draw a horizontal line at the bottom of the diagram connecting the 2 vertical parallel lines to form a 9-sided polygon.
Sum of the interior angles = (9 - 2) * 180 = 1260
Sum of known angels in the diagram = 40 + 270 + 125 + 270 + 35 + 270 + 90 + 90 = 1190
Angle x = 1260 - 1190 = 70
You can find the alternate angles not given by subtracting from 360 the two 90 degree angles inside the adjacent squares, and the angle given. One set of alternate angles adds up to 200, while the others adds to 250, for a difference of 50 degrees. There is 180 degrees on the right parallel line, minus 90 degrees for the angle inside the square. In order for both sets of alternate angles to be equal, the final pair of alternate angles must have a difference of 50 degrees, giving us 70 and 20 degrees for angle x and its corresponding alternate angle pair, respectively.
90 - 40 = 50
125 - 50 = 75
90 - 75 = 15
35 - 15 = 20
90 - 20 = 70
We need to consider added lines of up to 180 degrees only.
Answer: 7 0
I got stuck so ended up thinking it through as a physical object, specifically considering the impact of the specified bottom angles vs their top counterparts.
I did this because intuitively it made sense to me that if you consider a line going from the left corner of the pink square to the right corner of the blue square (shown below in orange), it may not be perpendicular at the moment.
Each angle specified (40, 125, 35) will cause the orange line to shift up or down. If the right side is going to be parallel to the left, then we should be able to work out what the difference between the top angles and bottom angles, and then the difference between x and y shown below is what is going to 'correct' any difference.
The sum of the angles specified are 40 + 125 + 35 + x = 200 + x
The sum of the opposite angles to those will be 50 + 55 + 145 + y = 250 + y (you can just take away the 90 degree angles as required from 180 or 360)
If the lines on each side are parallel, these two must balance out, so 200 + x = 250 + y, so x = y + 50 (this is equation A)
Now we know that x + y + 90 = 180 as they lie on a straight line, so x + y = 90 (this is equation B)
Substitute equation A into B and you get:
(y + 50) + y = 90
=> 2y = 40
=> y = 20
Substitute this into equation A and you get x = 20 + 50 = 70.
I think thats wrong. George. it's actually pretty easy. it goes like this: x = 989 + 333° = 70°,
Log in to reply
we have 0. so, x = 70°, and on top of that. we can add ( x ) ( x ).
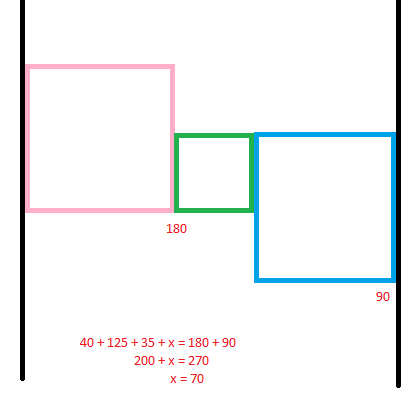
If we draw parallel lines between the opposite corners of a square, then the angles subtended at the lines equal to 90. We can see that this is true, by drawing in the vertical angle in the in-between corner, and see that by alternate angles, these 2 angles sum up to the internal angle of a square, which is 90. (Do you see why? Draw the parallel line at the corner, and by alternate angles these 2 angles can be moved to the internal angle.)
So, if we draw in parallel lines at the point of contact, then all of these angles add up to 9 0 × 3 = 2 7 0 .
Then we have, 1 2 5 + 3 5 + 4 0 + x = 2 7 0 , so x = 7 0 .