Three tangent circles in a triangle
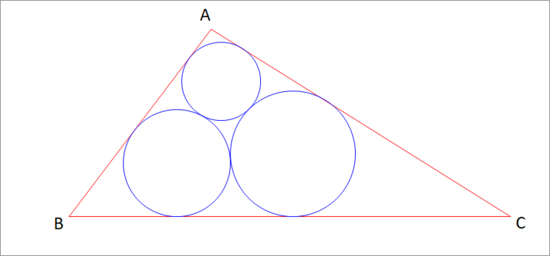
In , . Three tangent circles are to be inscribed in the triangle as shown in the figure above. If is the sum of their radii, enter
The answer is 528360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radii of the three circles be r A , r B , r C . Label the points of tangency along B C as P , Q as below:
Since the centre of the circle nearest B lies on the bisector of ∠ B , we have B P = r B cot 2 B . Similarly, C Q = r C cot 2 C .
By Pythagoras, P Q 2 = ( r B + r C ) 2 − ( r B − r C ) 2 , so that P Q = 2 r B r C .
Putting all these together, B C = r B cot 2 B + 2 r B r C + r C cot 2 C
We can use the same approach on the other two sides to find C A = r C cot 2 C + 2 r C r A + r A cot 2 A and A B = r A cot 2 A + 2 r A r B + r B cot 2 B
Since we know the sides of Δ A B C , we can work out the required angles as well. I didn't find a nice algebraic solution so plugged the equations into Wolfram|Alpha to find r A = 1 . 3 3 5 9 6 … , r B = 1 . 8 1 8 2 7 … , r C = 2 . 1 2 9 3 7 …
giving an answer of 5 2 8 3 6 0 .