Tic Tac Toe- part 1
In the game of
tic tac toe
, also called "dot and cross" game, there is a
grid, and (say that) the player who makes first move makes a "cross". The player who plays next makes a "dot" . A player wins if his marks (dot or cross) come three in a row, that could be diagonally or vertically or horizontally.
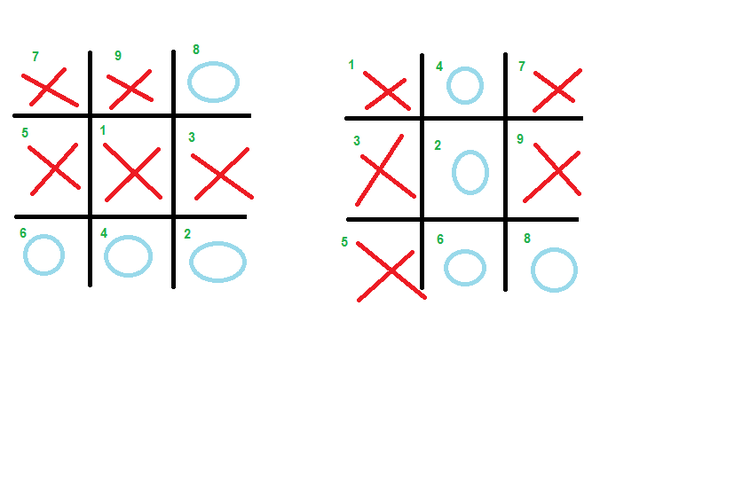
If the players just play for completing the whole grid ,i.e play even after any 1 wins, then how many Final positions of the game are possible ?
Two of such examples are given in figure, players are not playing for winning, they are playing just to fill all the boxes.
(There will be 5 crosses and 4 dots in the final position as the player who makes first move will play 1 turn more.)
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Not very difficult, the final position will have 5 c r o s s e s , and 4 d o t s . Thus there will be
( 5 9 ) = ( 4 9 ) = 1 2 6 different final positions .