Tic-Tac-Toe without the middle square

Relevant wiki: Tic Tac Toe

Suppose the first player, controlling X's were to win a game. Then, the turn before he wins, he would need to create a 'double threat', as otherwise his attack would have been blocked. In order to create a double threat, X will need to place his piece on a corner square, as edge squares can only threaten 1 row or column at a time, since they are only on 1 row or column. From this position, X will need to create 2 threats, one in the same column, and one in the same row. (Some ways X can do so are depicted below)

Now, to create a double threat in the top and left rows, O must have no pieces in these rows. Hence, O can guarantee X's defeat by using the first 2 turns to take 2 different corners. So the first player cannot win.

Additionally, it is clear that the second player cannot win, as we can use the same strategy. Hence, if both players play optimally, there can be no winner.

( $O$ and $X$ ) no one of them haven't any force to win the game

The above $(GIF)$ shows a scenario for our condition.

• The central cell is the most stratigical cell of the game.

• If we block the central cell of the game then no body won't be can win the game. Each play only can avoid from losing.

Note: The above Theory only respond for that each player play optimally the game.

Relevant wiki: Tic Tac Toe

The only way to win even if both players play optimally is to force a trap, where two two-in-a-rows are created at once. There are many ways to do this, but they all fall into one of the three types shown below:

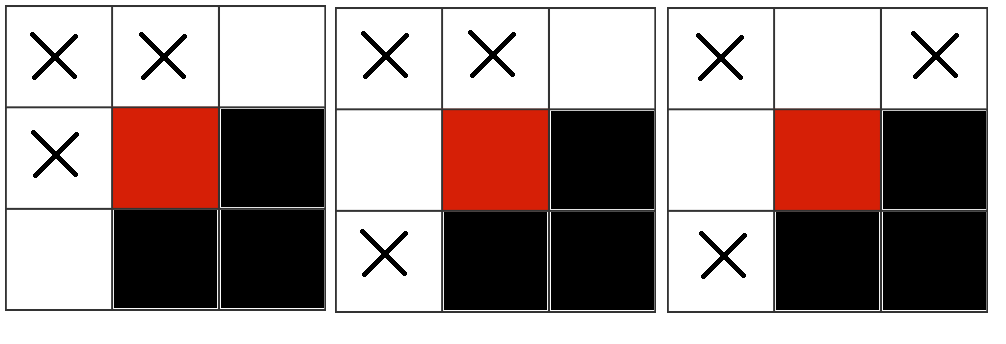
The white squares must also be empty, and the X in the top-left corner must be placed last. O has to block the trap before X places their final piece.

If X places their piece in a square between two corners (options 1 and 2), O can simply block that entire row by placing their piece in an adjacent square. If X places their piece on a corner square (options 2 and 3), O can play in the opposite corner, which must also be part of the trap. Therefore, O can block any trap X tries to make and vice versa. The game must end in a draw.

I propose to consider another modified version of tic-tac-toe, which I'll call the n-circular modified tic-tac-toe, for lack of a better name: The rules of placement and winning are the same, whoever got first their three marks in a row, win. 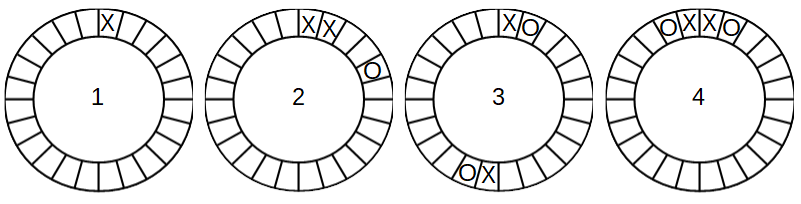I assume the first player (mark X) have the advantage because he is the first to put its mark. Any place where he puts the first mark (fig.1), he creates a single segment of unoccupied places limited only by its mark, which for convenience I call a XX segment . The second player (mark O) must answer with a connected mark to the first because if not, next time, the first player will build a -XX- configuration where we can win by marking one the two placeholders "-" (fig.2). But by answer with a connected mark, the segment XX will be converted into a XO one, one terminated by two different marks.

The aim of the first player is to get marks dispositions like X-X (a XX segment) or XX- and playing in the placeholder -, win the game. The strategy to defend against this is simple: Each time the first player puts his mark into a XO segment (like X----O),...

1) ...creating an XX segment (like in X--X-O), the second player answers with a connected mark to the previous in such a way that it converts that XX segment into a XO one (like X-OX-O). This way, the first player never gets the chance to play into a XX segment, since the second player will destroy them as fast as the first creates them. (fig.3)

2) ...connected with its own mark (like in XX----O), the second will again connect this mark with his own, converting the XX segment into a OO. The roles are reversed, and now, the first player must be the one in the defensive. This happens because, since the defender player are always connecting to the previous move, all segments are terminated by pairs OX, and extending it with a X (OXX_) doesn't creates a double threat. (fig.4)

The tic-tac-toe of the problem is the same as an 8-circular modified tic-tac-toe with the following difference: the set of winning configurations of the former is a subset of the later. So, if it is not possible to warrant a winning configuration in the 8-circular modified tic-tac-toe, it is not possible to get it in the modified tic-tac-toe of the problem either.

We might however question if by having less winning configurations, this allows the second player to ignore certain threats and win the initiative. But this doesn't do it, since we already saw that to won the advantage is not enough to win the game.

Once the center is blocked, there are only two types of plays: corner and edge. It is obvious that player 2 cannot win because if there is a strategy, player 1 can execute that strategy. So the question boils down to: can player 1 win? Because there are 4 edges, there are 4 conditions to win: left, right, top, bottom. Each corner play creates/eliminates 2 possibilities and each edge play creates/eliminates 1 possibility to win. So here is player 2's strategy:

First play: play a corner where the opposite corner is not occupied and there is a shared edge between this play and player 1's first play. It must be possible because there are 2 pairs of opposite corners and player 1 has only made 1 play. If player 1 made an edge play, that play becomes useless because the possibility has been taken out, so player 1's optimal strategy would be to make a corner play.

Second play: If opposite corner is not occupied, play it. Game over because there is no way to win for player 1. If it is occupied, it must be the last play of player 1. The board will look like this

There is only one sensible play for player 2 now, which is block player 1.

Third play: the question marks are unoccupied after the second play. So for the third play, player 2 needs to take at least one of the question mark and the game becomes unwinnable. Because there are two question marks, player 1 cannot occupy both in one play. Hence the game is unwinnable. QED.

This is a bad question. It's theoretically possible for either to win or a stale. If the question is about the optimal tic tac toe strategy than nothing changes by blocking out one space. Doing so confused the purpose of the puzzle.

Since there is an even number of boxes to play, each player will get the same number of moves during the game. Therefore if both players play optimally, neither the first nor second player has a greater chance of winning.

No one can win if both people are decent. If x goes bottom corner of just has to go opposite and no one can win, Henceforth the game being undoable.

The middle is the best place for moves. Blocking it means that the second player just has to block all the time or he loses. If he blocks all the time, it will be a draw.

A player requires three chances to win but a opponent player can stop other player to win in 2 chances by marking on the diagonal squares .

More columns got blocked, less possibility for anyone to win or loose. Hope this helps.

If the game is played optimally, it will be always a draw because there are no diagonal wins.

Actually, if the game is played optimally, nobody can win as the players are of equal calibre and it doesn't really matter whoever plays first.

Let’s say x starts first. X puts it on one corner. O puts it next to it. If they keep on outing it next to each other, nobody would win.

El jugador 2 bloqueará los intentos del jugador 1 y este no puede hacer ningún truco porque la parte fundamental es la diagonal y está bloqueada.

Imagine taking the grid and arranging the boxes so that they are in a line.

Winning the game is now reduced to one-lined "connect 3".

The grid can be shifted back and forth, which is just another possible arrangement.

eg. [O][X][O][X][X][O][O][X]

Neither player can win, because it takes 3 turns to connect 3, but only 2 turns to block both sides of a symbol.

You can think of it as neither player having enough tempo.