Tick Tack Toe #1

Relevant wiki: Tic Tac Toe

Hence $\color{#3D99F6} \boxed{\text{O can force a win}}$

Relevant wiki: Tic Tac Toe

First put O in any corner. Then, X is forced to be in the opposite corner. Now, put O in any other corner. Because there are now one row and one diagonal missing one, any one X picks will remain the other row or diagonal missing one.

O can go in any corner. Obviously, X is forced to block the win. If O went in a top corner, he is forced to go in the bottom corner in the same column, thereby creating a fork. If O went in a bottom corner, he can force a win by playing in either of the other two cells in the same column.

Yet another way to win is to take the left or right edge cell and then an adjacent corner. In other words, O can force a win by going anywhere except the top.

Side comment: I was taught as a child that O goes first, but a lot of resources take the position that X goes first (or that there's no set rule about it). This is one of the few instances I've seen in recent times of O going first. (I wonder if there's any correlation between this and whether people call the game "noughts and crosses", "tic-tac-toe" or some other name.)

The trick is to create a situation where there are two ways for O to win, but X can only block one. For instance, imagine O plays the following move:

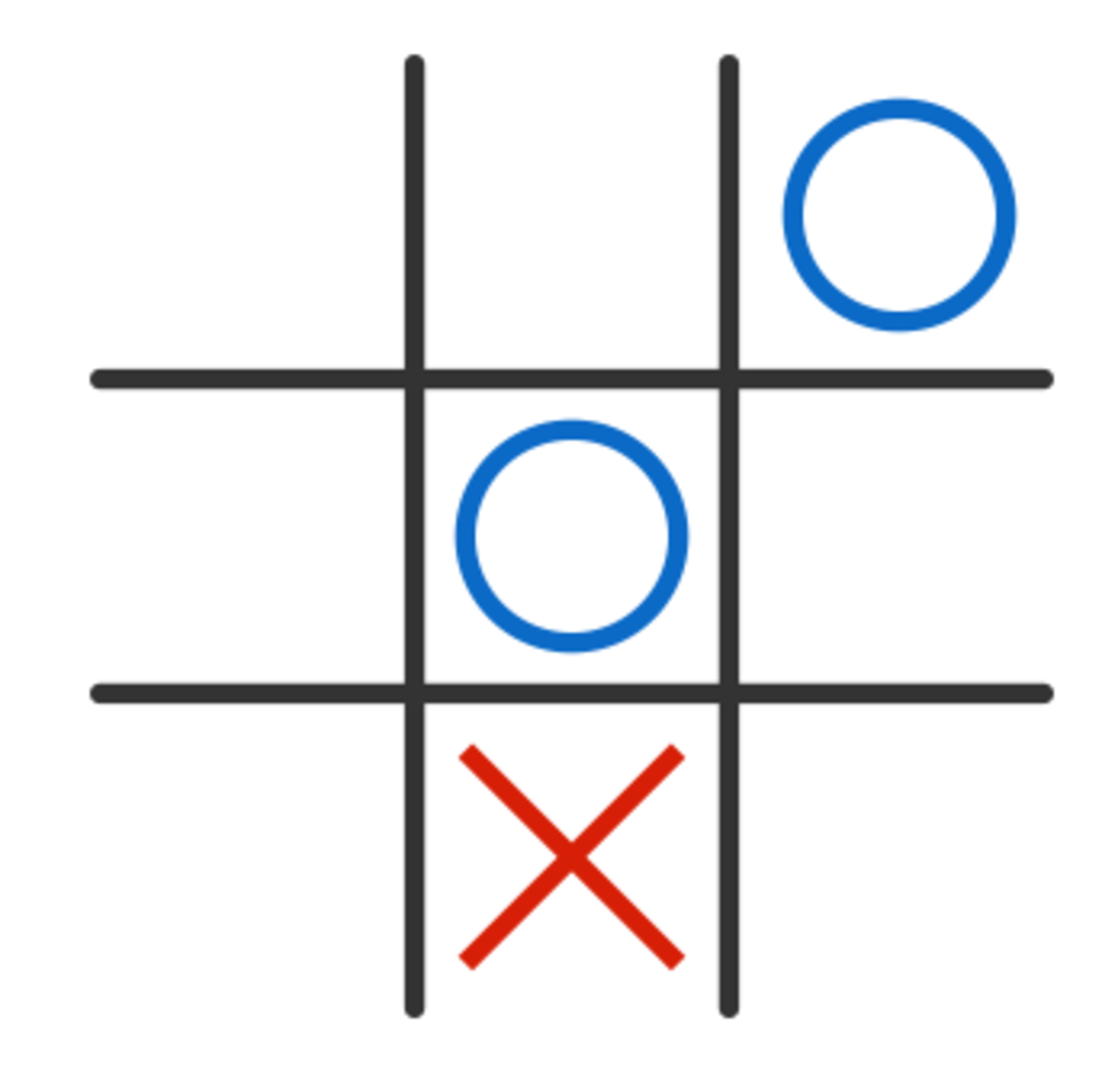
Now X is forced to play in the bottom left to prevent a three in a row:

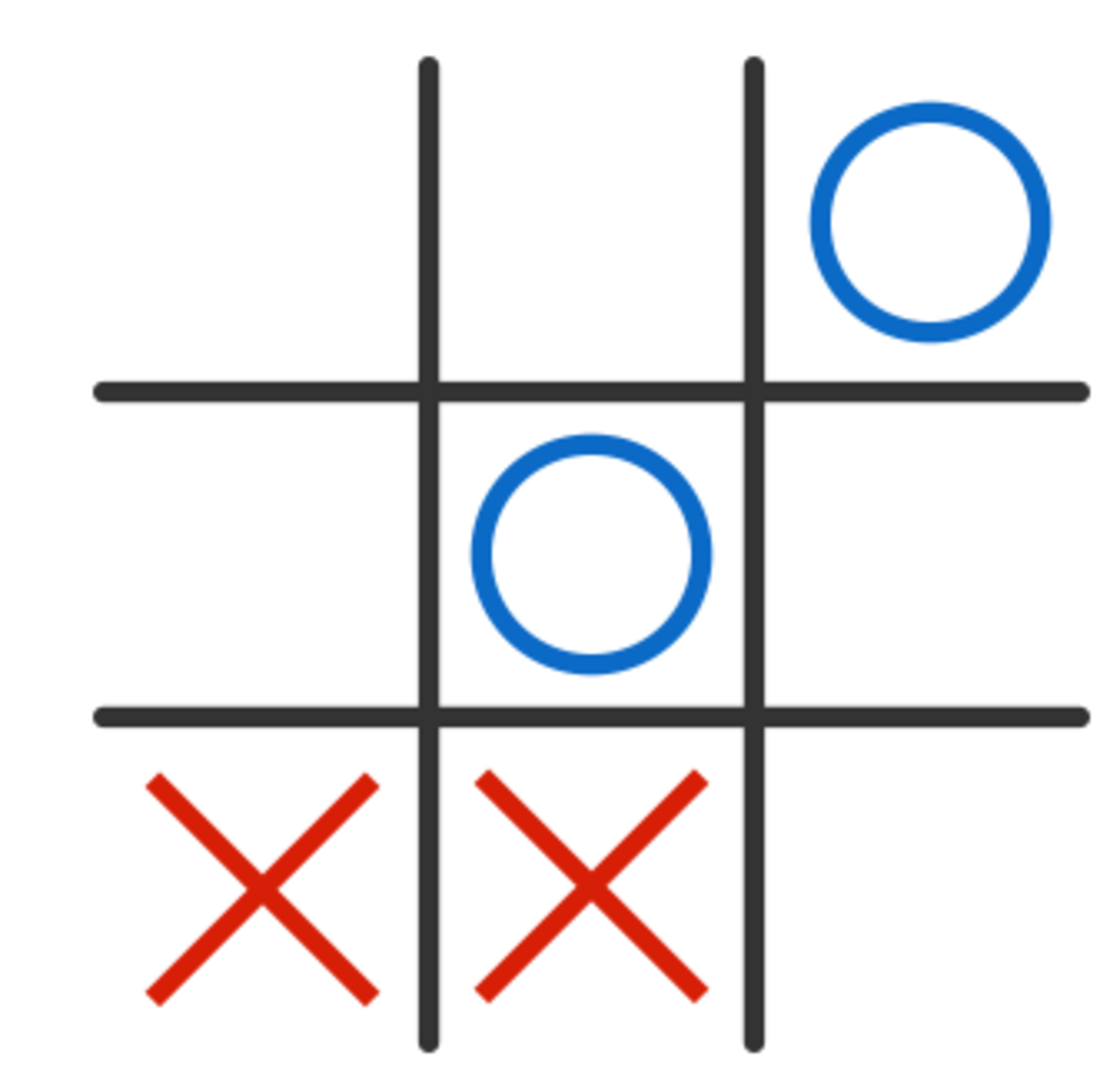
Now O plays this move:

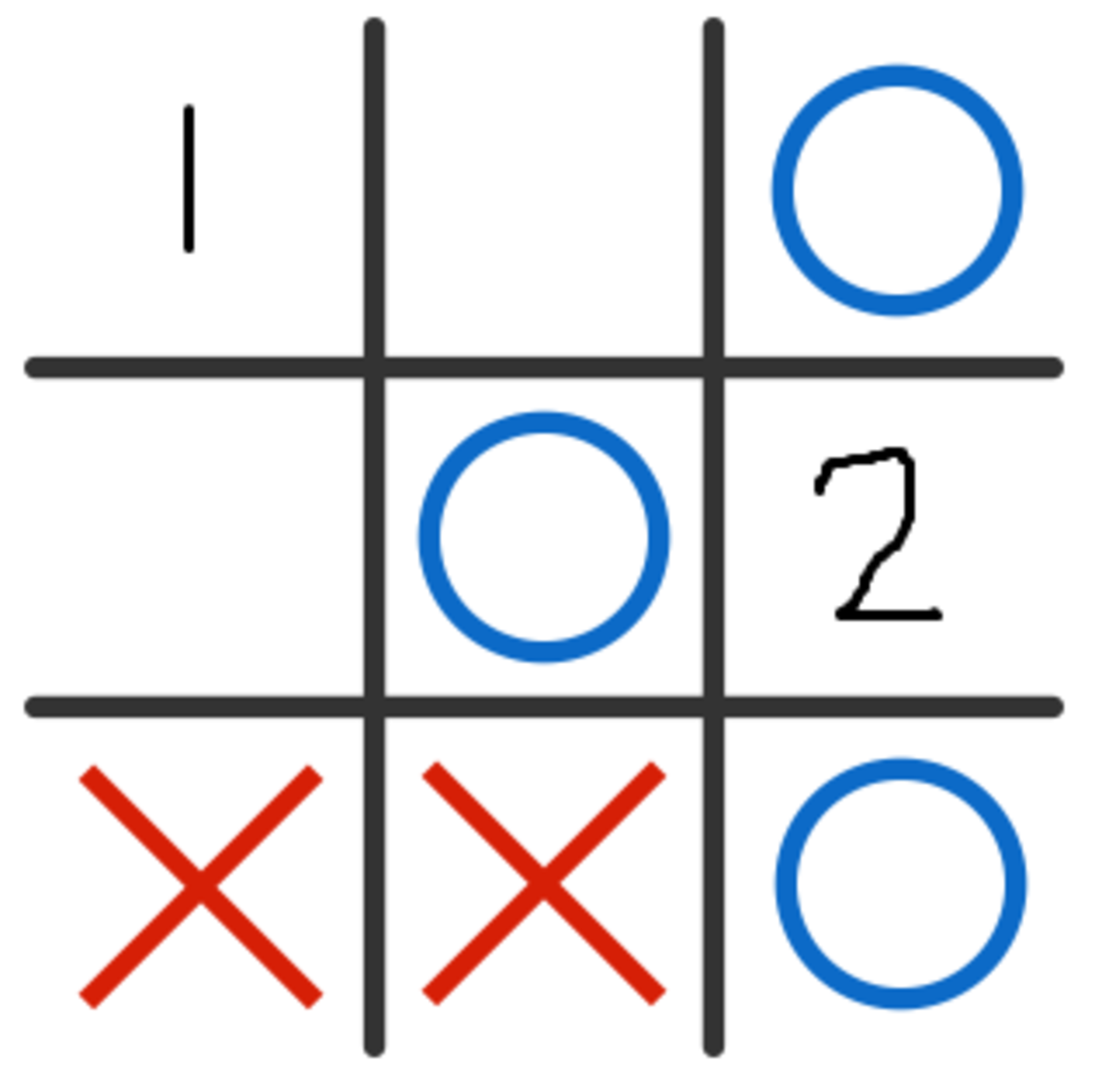
If X puts their move on square 1, O plays their move on square 2. If X puts their move on square 2, O plays their move on square 1. Therefore, O forced X into a loss.

The answer is YES , because if the first player (the O) moves to any of the upper corners, regardless of the side, the other player (the X) is forced to defend, hence leaving the attacker (O) two choices. Here is a visual representation:

First Move

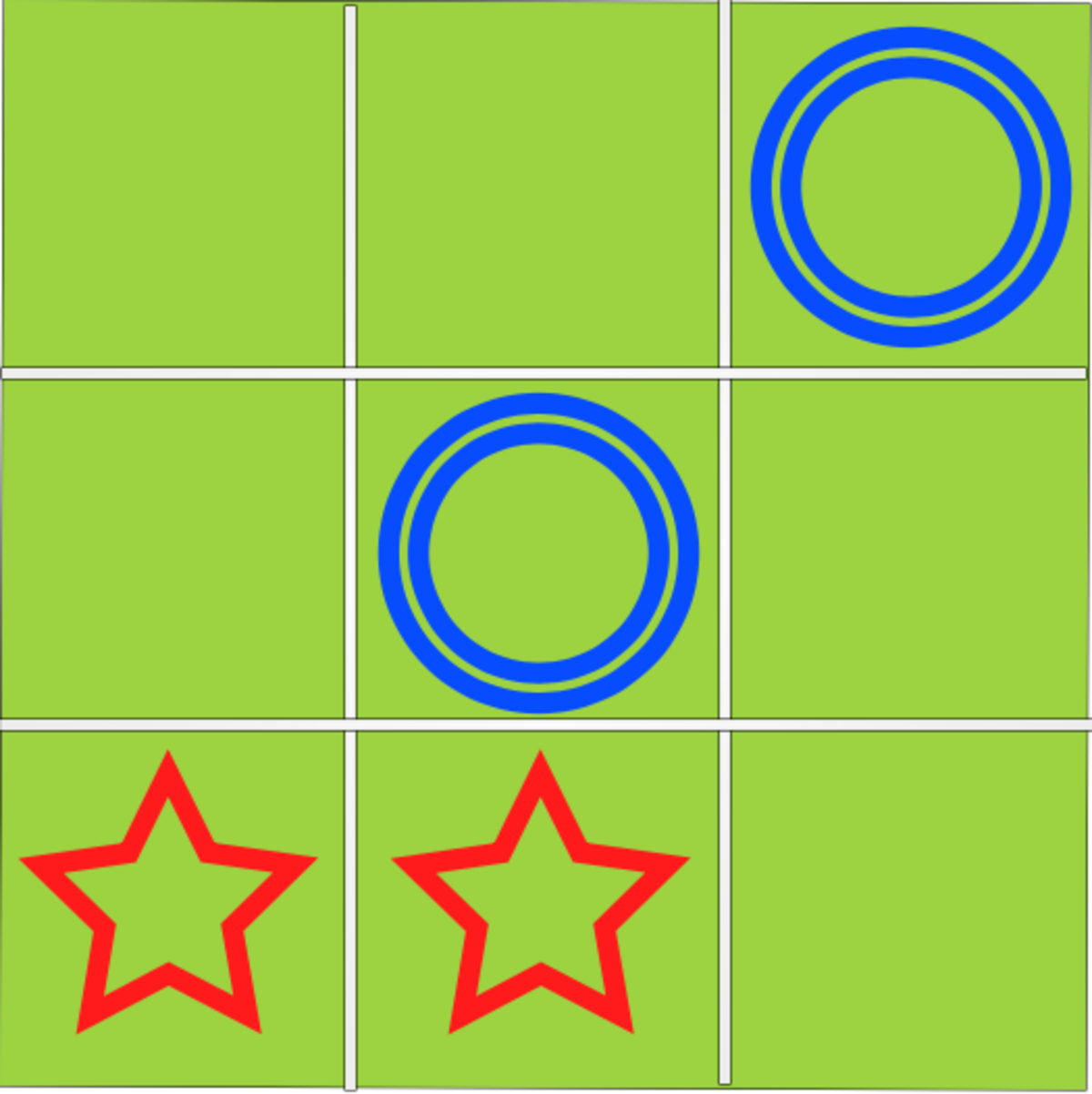Second Move

Third Move

Now it is pretty obvious that O has two ways to win the game, thus there is nothing left to do for the defender.

It is possible but sometimes, it depends on the other players moves.

If both palyers are playing optimally the game , $\color{#3D99F6}{O}$ will be win the game.

Because $\color{#3D99F6}{O}$ select the central cell of the game . Central cell is the strategical cell of $\text{(Tic tac toe)}$

Two case will be support the $\color{#3D99F6}{O}$ .

One case is in below :

There is just one move...just put O on any corner...and no matter how much you try O will always win...

If O goes into either space to the right or left, X has to block. O then goes to the appropriate corner, X can only block one of two possible moves.

Whoever moves first can always win in tic-tac-toe. The second move by the first player controls where the second player makes their second move.

Put O anywhere, and then form a triangle next turn in such a way that there are two ways to win. This is a force win, and there is no way to prevent it.

Put O on either side of the middle row. Then place an O either above or below it. You have forced a win.

1.O choses the Lower left corner. 2. X Must counter with upper right corner. 3. Then o goes in Middle left. 4a. If x goes in top left then o wins horizontal middle. 4b. If x goes middle right then o wins left vertical

As long as Circle's next move is on the corner, it is going to win.

There's an even quicker solution: put an O on the top left corner, which forces X to be put on the lower right corner. In turn that forces O to be put in the lower left corner, assuring the win for O.

As long as 'O' does not go into the top centre square with its next move, it should be able to win.

In TicTacToe the first player must take the center or they will lose. The second player must take a corner or THEY will lose.