Tiling a Grid

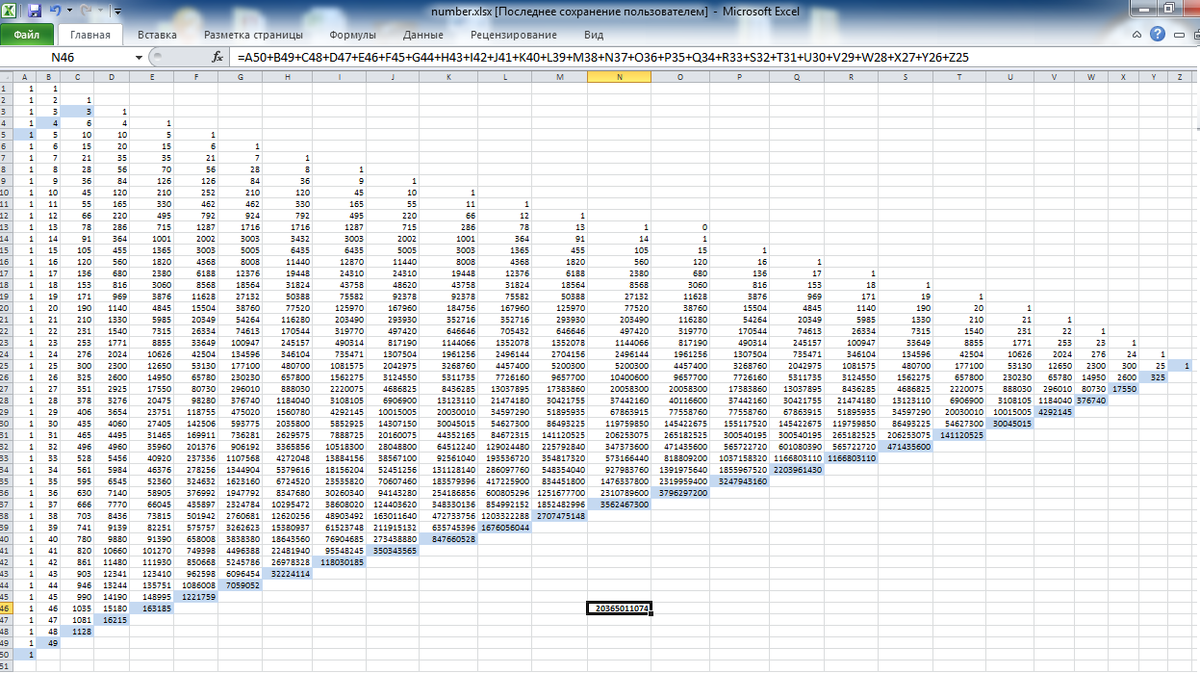
Let $t(n)$ be the number of ways of tiling a $2\times n$ grid.

Now, all of these tilings have either one $2\times 2$ tile or a vertical pair of $1\times 1$ tiles at their rightmost position. We see that there must be $t(n-2)$ of the first type and $t(n-1)$ of the second. So we have the relationship $t(n)=t(n-1)+t(n-2)$ (for $n>2$ ).

Clearly $t(1)=1$ and $t(2)=2$ , so the $t(n)$ are just the Fibonacci numbers.

$F_{50}=\boxed{20365011074}$ , so this is the required answer.

I use Excel for Binomtable.