Tiling An Irregularly Shaped Region
Consider the region in the picture below, where the dark-red shaded square indicates a hole in the region.
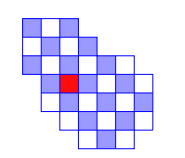An irregularly shaped grid with one hole
Is it possible to tile this region with 1-by-2 dominoes?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Proof by contradiction. Assume that such a configuration is possible.
In the above image, consider the blue cells labelled 1, 3, 5, 7, 8, 10. They must be tiled up with the white celles labelled 2, 4, 6, 9, 11. Since there are only 5 white cells and 6 blue cells, this tiling is not possible.
The deeper mathematical theory is known as the hall marriage theorem . It states that the necessary and sufficient condition for a perfect matching of a bipartite graph ( V 1 × V 2 , E ) to exist, is that given any subset A 1 of V 1 , the size of the set of vertices with edges to A 1 must be at least as large as the size of A 1 . Thus, to show that such a configuration is not possible, we just need to find a subset that is connected to a smaller set, like we did above with the 6 blue cells.