Tilted and shrunk

WLOG, let the side length of $\triangle ABC$ be $1$ . If $BF = x$ , then $BD = 1 - x$ .

By symmetry (or a simple congruency proof) the areas of $\triangle BFD, \triangle CDE$ and $\triangle AEF$ are equal, so the area of $\triangle BFD$ is one-sixth of the area of $\triangle ABC$ . Then

$\begin{aligned} \dfrac{1}{2}(BF)(BD) \sin \angle FBD &= \dfrac{1}{6} \cdot \dfrac{1}{2}(AB)(BC) \sin \angle FBD \\ \\ (BF)(BD) &= \dfrac{1}{6}(AB)(BC) \\ \\ x(1 - x) &= \dfrac{1}{6}(1)(1) \\ \\ 6x^2 - 6x + 1 &= \ 0 \\ \\ x &= \dfrac{3 \pm \sqrt{3}}{6} \end{aligned}$

Since the area of $\triangle DEF$ is half the area of $\triangle ABC$ , the ratio of the side lengths will be $\dfrac{1}{\sqrt{2}}$ , so $DF = \dfrac{1}{\sqrt{2}}$ . Then applying Sine Law to $\triangle BDF$ ,

$\begin{aligned} \dfrac{\sin \angle BDF}{BF} &= \dfrac{\sin \angle FBD}{DF} \\ \\ \dfrac{\sin \alpha}{\left( \dfrac{3 \pm \sqrt{3}}{6} \right)} &= \dfrac{\left( \dfrac{\sqrt{3}}{2} \right)}{\left( \dfrac{1}{\sqrt{2}} \right)} \\ \\ \sin \alpha &= \dfrac{\sqrt{6} \pm \sqrt{2}}{4} \\ \\ \alpha = \dfrac{\pi}{12} \qquad &\text{OR} \qquad \alpha = \dfrac{5 \pi}{12} \end{aligned}$

But we know $\alpha < \dfrac{\pi}{3}$ because when $\alpha = \dfrac{\pi}{3}$ , the area of $\triangle DEF$ is clearly one-fourth of the area of $\triangle ABC$ . So our answer is $\alpha = \boxed{\dfrac{\pi}{12}}$

Let $s$ be one of the sides of $\triangle ABC$ . Since the ratio of the areas of $\triangle ABC$ and $\triangle DEF$ is $\frac{2}{1}$ , the ratio of the sides is $\frac{\sqrt{2}}{1}$ , which means one of the sides of $\triangle DEF$ is $\frac{\sqrt{2}}{2}s$ .

Let $O$ be the center of both equilateral triangles. Then draw $\triangle BDO$ .

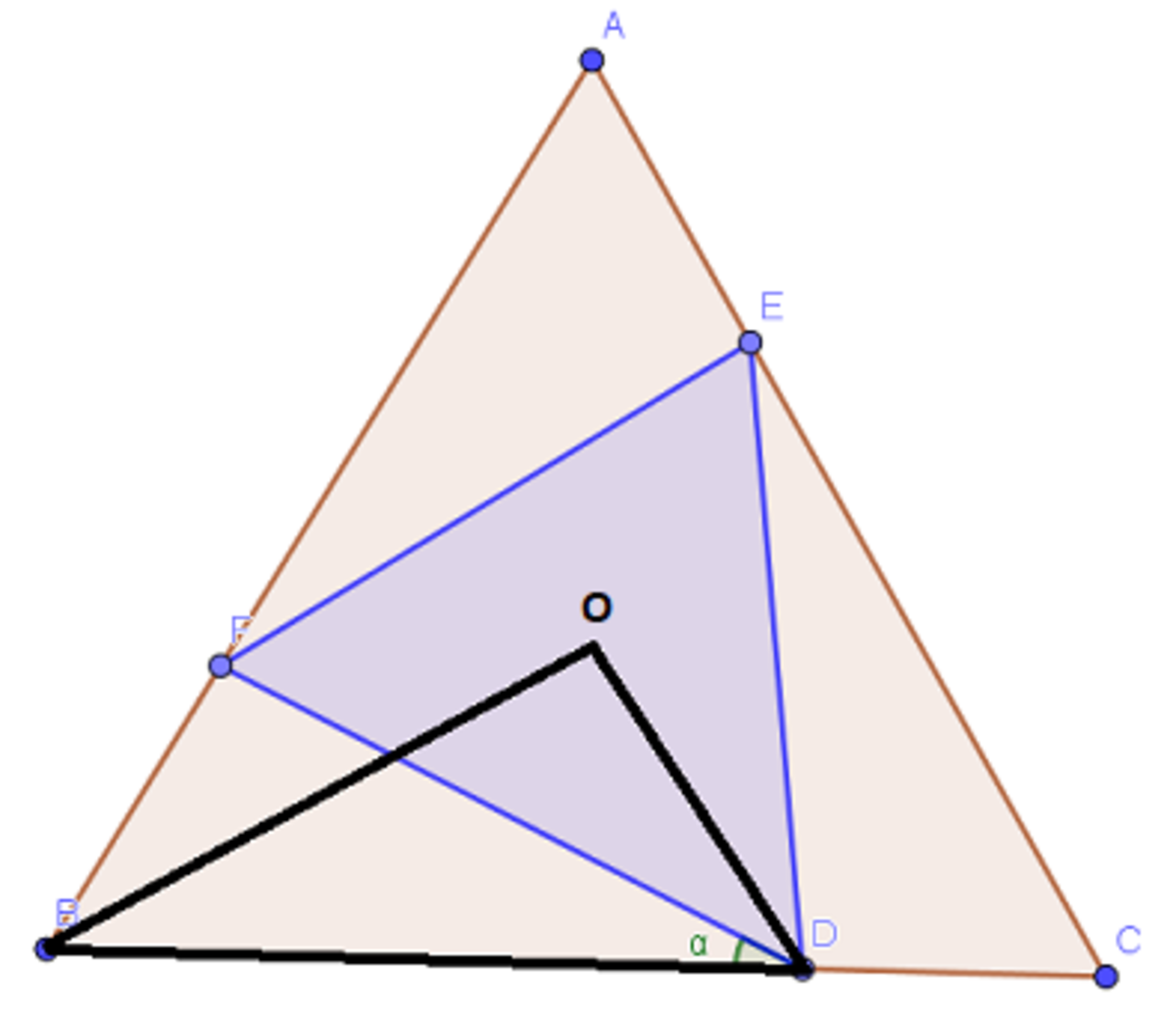
Since $BO$ is the length between the center and vertex of an equilateral triangle of side $s$ , $BO = \frac{\sqrt{3}}{3}s$ , and $\angle CBO = \frac{\pi}{6}$ . Since $DO$ is the length between the center and vertex of an equilateral triangle of side $\frac{\sqrt{2}}{2}s$ , $DO = \frac{\sqrt{6}}{6}s$ , and $\angle FDO = \frac{\pi}{6}$ . Then by law of sines, $\frac{\sin \angle DBO}{DO} = \frac{\sin \angle BDO}{BO}$ , or $\frac{\sin \frac{\pi}{6}}{\frac{\sqrt{6}}{6}s} = \frac{\sin \angle BDO}{\frac{\sqrt{3}}{3}s}$ , which solves to $\sin \angle BDO = \frac{\sqrt{2}}{2}$ .

Assuming $\angle BDO$ is an acute angle, $\angle BDO = \frac{\pi}{4}$ , and $\angle FDB = \angle BDO - \angle FDO$ $=$ $\frac{\pi}{4} - \frac{\pi}{6}$ $=$ $\boxed{\frac{\pi}{12}}$ .

Using Law of Sines, we have 2 equations to solve for 2 unknowns

$\dfrac { x }{ Sin(y) } =\dfrac { \frac { 1 }{ \sqrt { 2 } } }{ Sin(60) }$
$\dfrac { 1-x }{ Sin(120-y) } =\dfrac { \frac { 1 }{ \sqrt { 2 } } }{ Sin(60) }$

which gets us $y=15$ degrees

Since we are finding the measure of an angle, we may assume $AB=BC=AC=1$ and we also get that $EF=FD=DE=\dfrac{\sqrt{2}}{2}$ .

Notice that $\Delta EAF \cong \Delta FBD \cong DCE$ because of the ASA Postulate. So let $BD = 1-FB=x$ .

Applying Law of Cosines on $\Delta FBD$

$(\frac{\sqrt{2}}{2})^2 = x^2 + (1-x)^2 - 2x(1-x)\cos{60}$

$\implies x = BD = \dfrac{3+\sqrt{3}}{6}$

$\implies 1-x = BF = \dfrac{3-\sqrt{3}}{6}$

Now applying Law of Cosines again on $\Delta FBD$ but with $\angle FBD = \alpha$

$(\frac{3-\sqrt{3}}{6})^2 = (\frac{\sqrt{2}}{2})^2 + (\frac{3+\sqrt{3}}{6})^3 - 2(\frac{\sqrt{2}}{2})(\frac{3+\sqrt{3}}{6})\cos{\alpha}$

$\implies \cos{\alpha} = \dfrac{\sqrt{6}+\sqrt{2}}{4}$

$\implies \boxed{\alpha = \dfrac{\pi}{12}}$ .