Tilted conical cup - new water depth
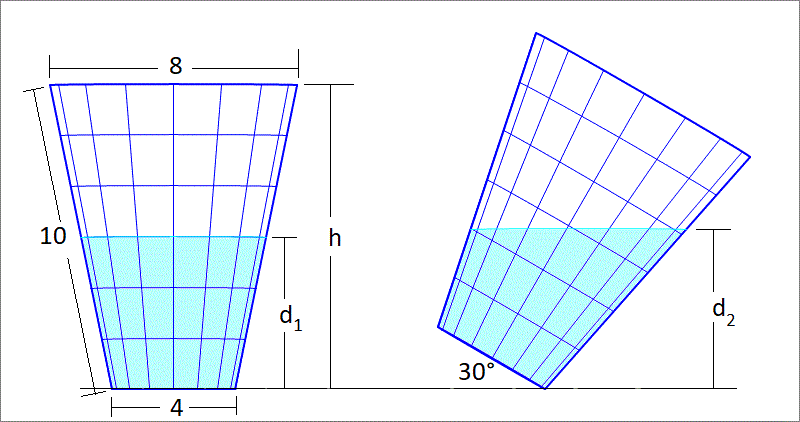
A water cup is in the shape of a conical frustrum with bottom diameter 4 cm, and top diameter 8 cm, and slant height 1 0 cm. It is filled to half its height with water, then the cup is tilted by 3 0 ∘ . Find the new depth (in centimeters) of water in the tilted cup (this is d 2 in the image above, drawn to scale). If the new depth is denoted by d then find ⌊ 1 0 3 d ⌋
Details and Assumptions:
- You may need the following formulas for the semi-minor and semi-major axes lengths of the water surface ellipse.
Semi-minor axis length = a = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
Semi-major axis length = b = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
Where z 0 is the distance between the apex and the intersection point of the axis with the intercepting plane. θ is the semi-vertical angle of the cone, i.e. the angle between the axis of the cone and its surface. Finally, ϕ is the acute angle between the axis of the cone and the normal vector to the intersecting plane. For completeness (although you won't need this in this problem), the distance between the center of the ellipse and the point where the axis of the cone meets the cutting plane is given by v 0 ,
v 0 = 1 − sin 2 ϕ sec 2 θ z 0 sin ϕ tan 2 θ
These formulas were derived in the solution of this problem .
The answer is 5153.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We are given that the bottom radius is r 1 = 2 and the top radius is r 2 = 4 and the slant height is s = 1 0 , hence the height h = s 2 − ( r 2 − r 1 ) 2 = 9 6
The radius of the water surface before tilting is r 0 = 2 1 ( r 1 + r 2 ) = 3 , And from similar triangles, we deduce that height of the cone underneath the water surface is 2 3 h .
Hence, the original volume of the whole cone underneath the water plane is
V 1 = 3 1 π r 0 2 2 3 h = 2 1 π r 0 2 h
If we take the origin at the apex of the cone, then its equation is
z = a x 2 + y 2 = a r
since r 1 = 2 at the bottom and r 2 = 4 at the top and the difference in z is h = 9 6 , then 9 6 = a ( 4 − 2 ) , so that a = 9 6 / 2 = 2 4
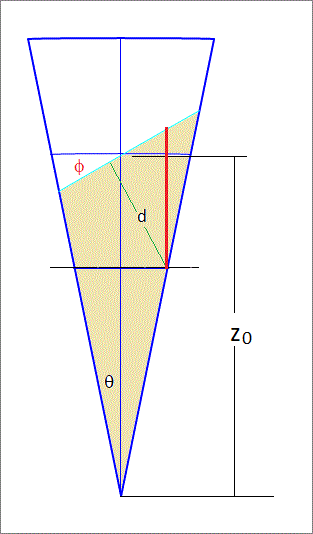
Next, the water surface in the tilted cup will cross the axis of the cup at an elevation of z = z 0 . This is shown in the attached image which shows
the cup after untilting. We need the find the volume under the blue line (plane). If we assume the x-axis is pointing towards the reader, then the y-axis is pointing to the right and the z-axis is pointing vertically up.
The equation of the plane of the surface of the water is z = tan ( 6 π ) y + z 0 where z 0 is yet to be determined.
To find the volume of the cone under this plane, we'll find its intersection
with the plane. Let t = tan 6 π = 3 1 , then
t y + z 0 = a x 2 + y 2
t 2 y 2 + z 0 2 + 2 t y z 0 = a 2 ( x 2 + y 2 )
Re-arranging,
y 2 ( a 2 − t 2 ) − 2 t y z 0 + a 2 x 2 = z 0 2
Completing the square,
( a 2 − t 2 ) ( y − t z 0 / ( a 2 − t 2 ) ) 2 + a 2 x 2 = z 0 2 + t 2 z 0 2 / ( a 2 − t 2 ) = z 0 2 ( a 2 ) / ( a 2 − t 2 )
This can be written as
x 2 / A 2 + ( y − y 0 ) 2 / B 2 = 1
where
y 0 = t z 0 / ( a 2 − t 2 )
A = z 0 / ( a 2 − t 2 ) 1 / 2
B = z 0 a / ( a 2 − t 2 )
This is the equation of the projection of the elliptical surface of water onto the xy plane.
The area of this region is
A 1 = π A B = π z 0 2 ( a 2 − t 2 ) 3 / 2 a
Hence the area of the cone underneath the water surface is
A 2 = sin θ A 1 = 5 A 1
And finally the volume is V 2 = 3 1 d A 2 = 3 1 z 0 sin θ ( 5 A 1 ) = 3 1 π z 0 3 ( a 2 − t 2 ) 3 / 2 a
Setting V 2 equal to V 1 , gives us z 0 . Solving for z 0 , we get z 0 = 1 4 . 5 9 4 5 1 9 5 2
Hence the altitude of water at r = r 1 is z ∗ = z 0 + t r − h = 1 5 . 7 4 9 2 2 0 0 6 − 9 6 = 5 . 9 5 1 2 6 1 0 8 7
And finally, the depth of water = z ∗ cos 6 π = 2 3 ( 5 . 9 5 1 2 6 1 0 8 7 ) = 5 . 1 5 3 9 4 3 2 8 6
which makes the answer ⌊ 5 1 5 3 . 9 4 3 2 8 6 ⌋ = 5 1 5 3
This is a follow-up of my solution of the previous problem . Refer to my previous solution to understand better the calculations in this solution.
First we find the volume of the half-filled water tumbler, V 2 1 = 3 2 6 π ( 6 3 − 2 3 ) ≈ 9 7 . 4 7 3 7 8 7 0 9 . Now we align the axis of the tumbler along the x -axis with its bottom along the z -axis. We note that the radius of the cross-section circle of the tumbler is given by r ( x ) = m x + 2 , where m = 2 4 1 . The volume of the water V ( x ) is the sum of the volume of a frustrum V 1 ( x ) and the volume of a "wedge" V 2 ( x ) . The volume of the frustrum is given by V 1 ( x ) = 3 2 6 π ( r 1 ( x ) 3 − 2 3 ) , where r 1 ( x ) is the base radius of the frustrum.
For the volume of the wedge V 2 ( x ) , we can make use of the result of the previous problem. Using the farthest point of the wedge from the z -axis as the reference for x , at x = 4 6 or at the brim of the tumbler, the water poured out when the tumbler is tilted at 3 0 ∘ is found to be V o u t ≈ 9 8 . 1 6 1 4 0 0 4 1 9 7 9 3 6 . The width of the wedge l ( 4 6 ) = 1 + 6 2 1 6 6 . This means that V 2 ( 4 6 ) = V 1 ( 4 6 ) − V 1 ( 4 6 − l ( 4 6 ) ) − V o u t ≈ 6 8 . 8 1 4 3 0 5 0 2 (volume of a frustrum with height l minus the volume of water poured out). We note that the shape of the wedge does not change with x , therefore V 2 ( x ) is directly proportional to r ( x ) 3 . Therefore we can find V 2 ( x ) = ( 4 r ( x ) ) 3 V 2 ( 4 6 ) .
Using the x -coordinate of the wedge's farthest end from the z -axis, the base radius of the frustrum r 1 ( x ) = m ( x − l ( x ) ) + 2 , where l ( x ) = 1 + 6 2 4 r ( x ) 6 . And the final formula is
V ( x ) = 3 2 6 π ( x − l ( x ) ) 3 − 8 ) + 6 4 r ( x ) 3 V 2 ( 4 6 )
We have to find the value of x , when V ( x ) = V 2 1 . As you can see the computation is very complex, I used a Microsoft Excel spreadsheet and manual iterations. The required x 1 ≈ 6 . 7 4 6 3 2 0 3 7 3 and the required d = 2 6 5 ( 5 2 6 × 2 3 − 5 1 × 2 1 ) x 1 ≈ 5 . 1 5 3 9 4 1 3 8 5 . Therefore ⌊ 1 0 3 d ⌋ = 5 1 5 3 .