Tilted cuboid tank - 1

Geometry Level pending

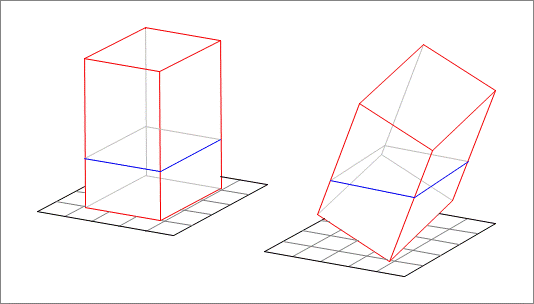
A cuboid tank is placed on the $xy$ plane, with its base centered at the origin. The base rectangle edges measure $5$ along the $x$ axis and $7$ along the $y$ axis. The height is $9$ . It is filled to $\frac{1}{3}$ of its height with water. This is shown on the left of the above figure. Then, it is tilted by $30^{\circ}$ about an axis of rotation passing through the base vertex $(\frac{5}{2} , -\frac{7}{2}, 0 )$ , and parallel to the vector $( \cos 60^{\circ} , \sin 60^{\circ} , 0 )$ . This is shown on the right of the above figure. Find the new height of the water surface relative to the $xy$ plane. If this new height is $d$ , enter $\lfloor 10^4 \hspace{3pt} d \rfloor$ .

The answer is 45556.

1 solution

Hosam Hajjir
Nov 10, 2020

From symmetry, it follows that the water surface after tilting must pass through the point $(0, 0, 3)$ (coordinates in the tilted frame of reference attached to the cuboid). Thus, all we have to do is rotate the vector $\mathbf{v} = (0, 0, 3) - (\frac{5}{2}, -\frac{7}{2}, 0) = (- \frac{5}{2}, \frac{7}{2}, 3 )$ about the given axis, and then take its $z$ -coordinate. The perpendicular unit vectors to the axis are $(-\sin 60^{\circ}, \cos 60^{\circ} , 0 )$ and $(0, 0, 1$ ). The components of $\mathbf{v}$ along $\mathbf{u}_1$ and $\mathbf{u}_2$ are $x = \mathbf{v} \cdot \mathbf{u}_1 = \frac{1}{4} (5 \sqrt{3} + 7 )$ , and $y = \mathbf{v} \cdot \mathbf{u}_2 = 3$ . Hence the rotated vector $\mathbf{v'} = (x \cos 30^{\circ} - y \sin 30^{\circ} ) \mathbf{u_1} + (x \sin 30^{\circ} + y \cos 30^{\circ} ) \mathbf{u}_2$ . Performing these calculations, results in,

$\mathbf{v'} = ( -1.637259526, 0.945272228, 4.555607966)$

Hence, the water level is $4.555607966$ , and this makes the answer $\lfloor 45556.07966 \rfloor = \boxed { 45556 }$

Tilted cuboid tank - 1

The answer is 45556.

1 solution

0 pending reports