Tilted cylindrical tank - 1
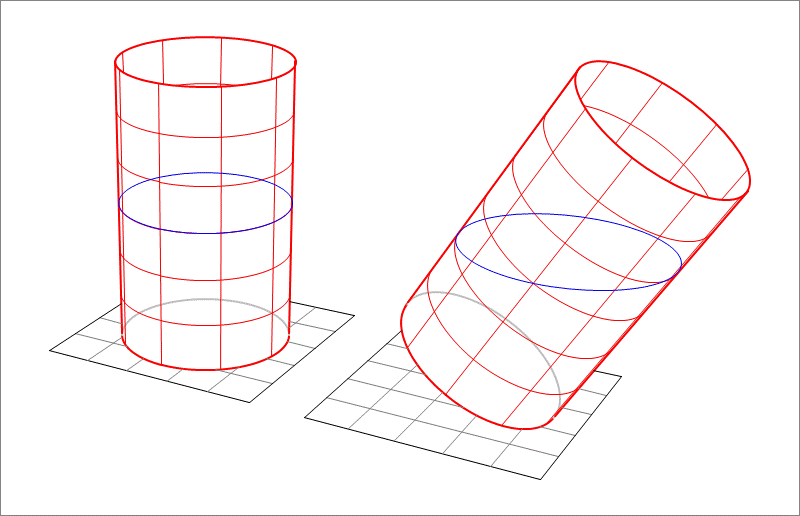
A cylindrical tank of base diameter and height is filled to half its height with water. This is shown on the left of the above figure. Then, the tank is tilted by as shown on the right of the figure. Find the new height of the water surface relative to the floor.
Note: This problem should not take more than minutes to solve.
The answer is 5.83.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
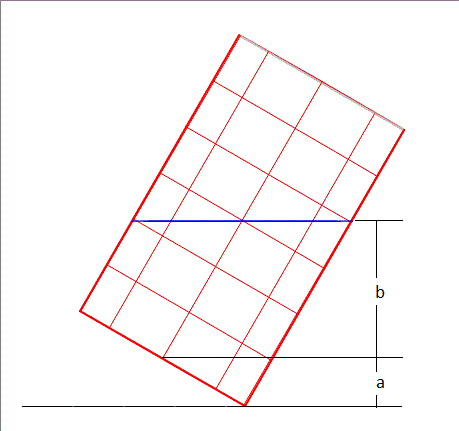
Since the cross-sectional area is a constant 3 2 π , after the half-filled cylinder is tilted, the volume of water above the mid-filled line (blue dash line) is same as the volume of water below the mid-filled line. Then the height of the right edge of the water surface above the mid-filled line measured along the right cylinder wall is 3 tan 3 0 ∘ = 3 . Then the new height of the water surface above the floor is ( 5 + 3 ) cos 3 0 ∘ = ( 5 3 + 3 ) / 2 ≈ 5 . 8 3 .