Tilted cylindrical tank - 2
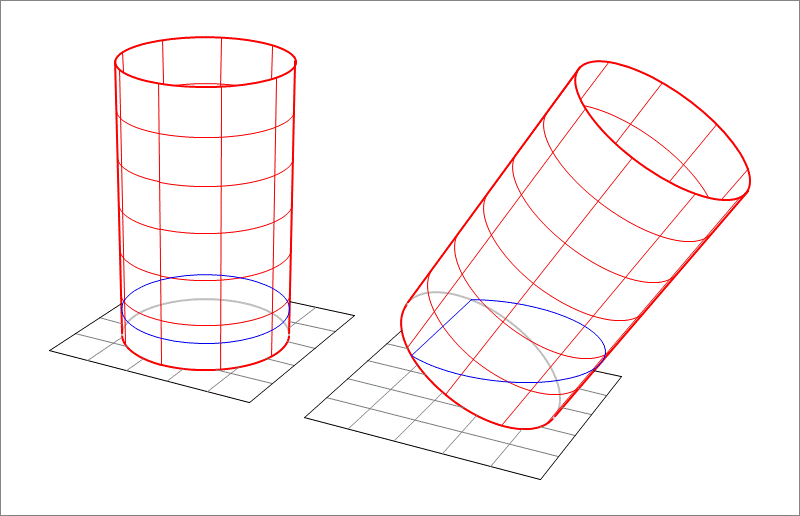
A cylindrical tank of base diameter and height is filled to one tenth of its height with water. This is shown on the left of the above figure. Then, the tank is tilted by as shown on the right of the above figure. Find the new height of the water surface relative to the ground.
The answer is 2.318.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Align the axis of the cylinder along the x -axis with the water surface of the tilted cylinder be symmetrically divided by the x z -plane. We note that the cross-sectional area perpendicular to the x -axis at x is A = π r 2 − r 2 cos − 1 ( r h ) + h r 2 − h 2 , where r = 3 and h ( x ) is a function of x (the blue line). Let the point on the water surface farthest from the z -axis be b . Then x − b h ( x ) + 3 = − 3 ⟹ h ( x ) = 3 ( b − x ) − 3 . As the volume of the water in the tank is 9 π , we have:
9 π = ∫ 0 b ( 9 π − 9 cos − 1 ( 3 h ) + h 9 − h 2 ) d x = 9 π b − 9 ∫ 0 b cos − 1 ( 3 h ) d x + ∫ 0 b h 9 − h 2 d x
Consider the last two integrals separately,
I = ∫ 0 b cos 3 h d x = 3 ∫ − 1 3 b − 1 cos u d u = 3 [ u cos − 1 u + ∫ 1 − u 2 u d u ] − 1 3 b − 1 = 3 [ u cos − 1 u − 1 − u 2 ] − 1 3 b − 1 = 3 [ ( 3 b − 1 ) cos − 1 ( 3 b − 1 ) − 3 2 b − 3 b 2 + π ] = ( b − 3 ) cos − 1 ( 3 b − 1 ) − 2 3 b − b 2 + 3 π Let u = 3 h ⟹ d u = 3 d h = − 3 d x Integration by parts
J = ∫ 0 b h 9 − h 2 d x = 9 3 ∫ cos − 1 ( 3 b − 1 ) π sin 2 θ cos θ d θ = 9 3 ∫ 3 2 3 b − b 2 0 v 2 d v = − ( 2 3 b − b 2 ) 2 3 Let cos θ = 3 h ⟹ − sin θ d θ = 3 d h = − 3 d x
Therefore we have:
9 π b − 9 ( b − 3 ) cos − 1 ( 3 b − 1 ) − 9 2 3 b − b 2 + 9 3 π − ( 2 3 b − b 2 ) 2 3 = 9 π
Solving it numerically, we get b ≈ 2 . 6 7 7 0 9 1 6 4 . And the height from the ground of the water surface h = b cos 3 0 ∘ ≈ 2 . 3 1 8 .