Tilted paraboloidal cup - new water depth
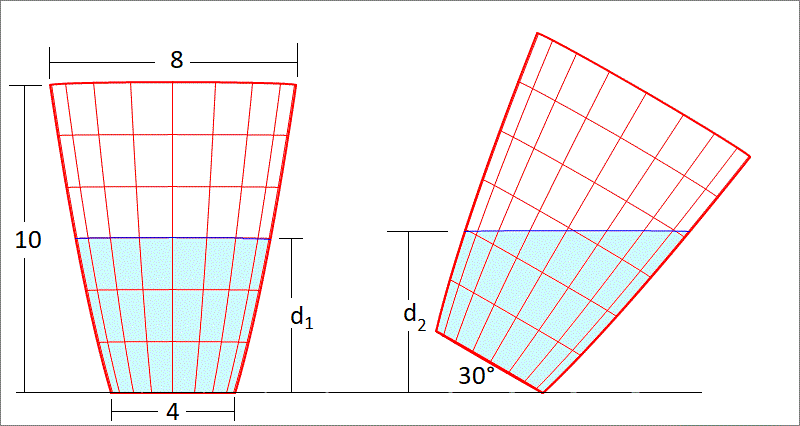
A cup is in the shape of a circular paraboloidal frustrum with bottom diameter 4 cm, and top diameter 8 cm, and height 1 0 cm. It is filled to half it height with water ( d 1 = 5 cm). Then, the cup is tilted by 3 0 ∘ . If the new depth of water is d cm (this is d 2 in the figure, drawn to scale) , find ⌊ 1 0 4 d ⌋
The answer is 52435.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 If we take the origin at the apex of the paraboloid, then its equation is
If we take the origin at the apex of the paraboloid, then its equation is
z = a ( x 2 + y 2 ) = a r 2
since r 1 = 2 at the bottom and r 2 = 4 at the top and
the difference in z is 1 0 , then
1 0 = a ( 1 6 − 4 )
so that a = 5 / 6
The volume of water in the cup plus the volume of the missing tip is
The z-value of the water surface in the cup before tilting is
z L = 1 / 2 a ( r 1 2 + r 2 2 ) = 5 / 1 2 ( 4 + 1 6 ) = 1 0 0 / 1 2 = 2 5 / 3
The corresponding value of r is r L = z L / a
V 1 = 2 π ∫ r = 0 r = r L a r 2 ⋅ r d r
= 1 / 2 a π r L 4 = 1 / ( 2 a ) π z L 2
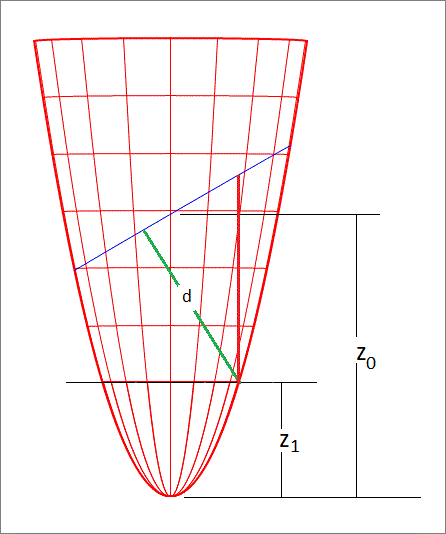
Next, the water surface in the tilted cup will cross the axis of the cup at
an elevation of z = z 0 . This is shown in the attached image which shows
the cup after untilting.
We need the find the volume under the blue line (plane).
If we assume the x-axis is pointing towards the reader, then the y-axis is
pointing to the right and the z-axis is pointing vertically up.
The equation of the plane of the surface of the water is z = tan 6 π y + z 0
where z 0 is yet to be determined.
To find the volume of the paraboloid under this plane, we'll find its intersection
with the plane. Let t = tan 6 π = 3 1 , then
t y + z 0 = a ( x 2 + y 2 )
t y / a + z 0 / a = x 2 + y 2
x 2 + ( y − t / ( 2 a ) ) 2 = t 2 / ( 2 a ) 2 + z 0 / a = R 2
This is the equation of the projection of the elliptical surface of water onto
the xy plane. Now we can find the volume by the following volume integral
V 2 = ∬ D ( t y + z 0 ) − a ( x 2 + y 2 ) d x d y
At this point, we'll make a change of variables x = r cos θ , y = t / ( 2 a ) + r sin θ
The determinant of the jacobian of this change of variables is simply r . Hence, the integral becomes
V 2 = ∫ θ = 0 2 π ∫ r = 0 R ( t ( t / ( 2 a ) + r sin θ ) + z 0 ) − a ( r 2 + t 2 / ( 4 a 2 ) + t r / ( a ) sin θ ) ) r d r d θ
Integrating over θ first, eliminates the terms containing sin θ , and multiplies the rest by 2 π . Hence,
V 2 = 2 π ∫ r = 0 R ( t 2 / ( 4 a ) + z 0 − a r 2 ) r d r
Integrating yields,
V 2 = π ( ( t 2 / ( 4 a ) + z 0 ) ( t 2 / ( 4 a 2 ) + z 0 / a ) − 2 1 a ( t 2 / ( 4 a 2 ) + z 0 / a ) 2 )
= 2 a 1 π ( t 2 / ( 4 a ) + z 0 ) 2 )
Setting V 2 equal to V 1 , gives us z 0
1 / ( 2 a ) π z L 2 = 2 a 1 π ( t 2 / ( 4 a ) + z 0 ) 2 )
implies that z 0 = z L − t 2 / ( 4 a )
The numerical value of z 0 = 2 5 / 3 − ( 1 / 3 ) ( 6 ) / ( 2 0 ) = 2 5 / 3 − 1 / 1 0 = ( 2 5 0 − 3 ) / 3 0 = 2 4 7 / 3 0
The depth of water is given the length of the green line in the figure which is related to the length of the red line by
L Green = cos 3 0 ∘ L Red
And we have
L Red = z 0 + t r 1 − a r 1 2
Hence, finally, the new depth of water is
d = cos 3 0 ∘ ( z 0 + t r 1 − a r 1 2 ) = 2 3 ( 2 4 7 / 3 0 + 2 / 3 − 2 0 / 6 ) ) ) ≈ 5 . 2 4 3 5 2
therefore, the answer is ⌊ 5 2 4 3 5 . 2 ⌋ = 5 2 4 3 5 .
Align the tumbler axis along the x -axis. The parabola is of the form z 2 = k a . Let x 0 be the x -coordinate of the bottom of the tumbler. Then
{ 2 2 = k x 0 4 2 = k ( x 0 + 1 0 ) ⟹ k = 1 . 2 and the equation of the parabola is z 2 = 1 . 2 x and x 0 = 3 1 0 .
We note that the radius r ( x ) of the cross-sectional circle is given by the parabola r ( x ) = 1 . 2 x and the volume of half-glass of water is given by:
V 2 1 = ∫ x 0 x 0 + 5 π r 2 d x = ∫ 3 1 0 3 2 5 1 . 2 π x d x = 0 . 6 π x 2 ∣ ∣ ∣ ∣ 3 1 0 3 2 5 = 3 5 π ≈ 1 0 9 . 9 5 5 7 4 2 9
The water surface in the tumbler is an ellipse. Align the major semiaxis in the x z -plane. Let the x -coordinates of the ends near and farther away from the z -axis be a and b respectively. For any a , the volume of water in the tumbler has two parts, for x < a , V 1 ( a ) = 0 . 6 π ( a 2 − 9 1 0 0 ) volume of the paraboloidal frustrum, and for x > a , V 2 volume of a "wedge" whose element δ x has a cross-sectional of a major circle segment of radius r ( x ) , center on the x -axis and its top edge at a height h ( x ) from the center. The cross-sectional area is given by A = ( π − cos − 1 ( r h ) ) r 2 + h r 2 − h 2 and the volume of the wedge is given by:
V 2 ( a ) = ∫ a b ( ( π − cos − 1 ( r h ) ) r 2 + h r 2 − h 2 ) d x
For a given a , h ( x ) is given by the blue line or h ( x ) = 3 ( a − x ) + 1 . 2 a and b = 5 5 a + 4 0 a + 2 . With r ( x ) , h ( x ) , a , and b known, we can find V 2 ( a ) by integration and V ( a ) = V 1 ( a ) + V 2 ( a ) . We need to find the value of a such that V ( a ) = V 2 1 . Since it is quite formidable to solve the integral manually, I used a Python code. At first I thought to write one that can do the iterations to find the required a but failed. So I did the iteration manually and get a ≈ 6 . 6 0 7 5 9 . From the z -intercepts of the red dash line and black line, we get d = ( z 1 − z 2 ) sin 3 0 ∘ ≈ 5 . 2 4 3 5 2 3 0 4 4 , ⟹ ⌊ 1 0 4 d ⌋ = 5 2 4 3 5 .