Tilted Square Numbers!
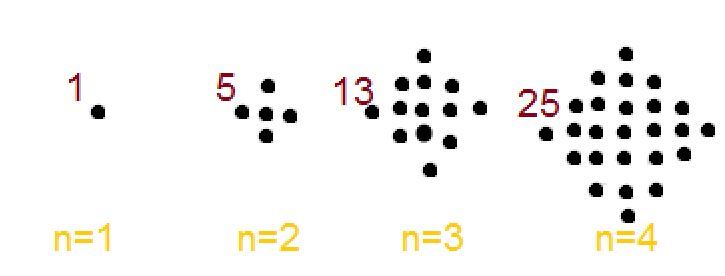 Let the numbers belonging to this sequence be known as tilted square numbers.
Find the sum of digits of the
1
0
1
0
3
th
tilted square number.
Let the numbers belonging to this sequence be known as tilted square numbers.
Find the sum of digits of the
1
0
1
0
3
th
tilted square number.
The answer is 9001.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
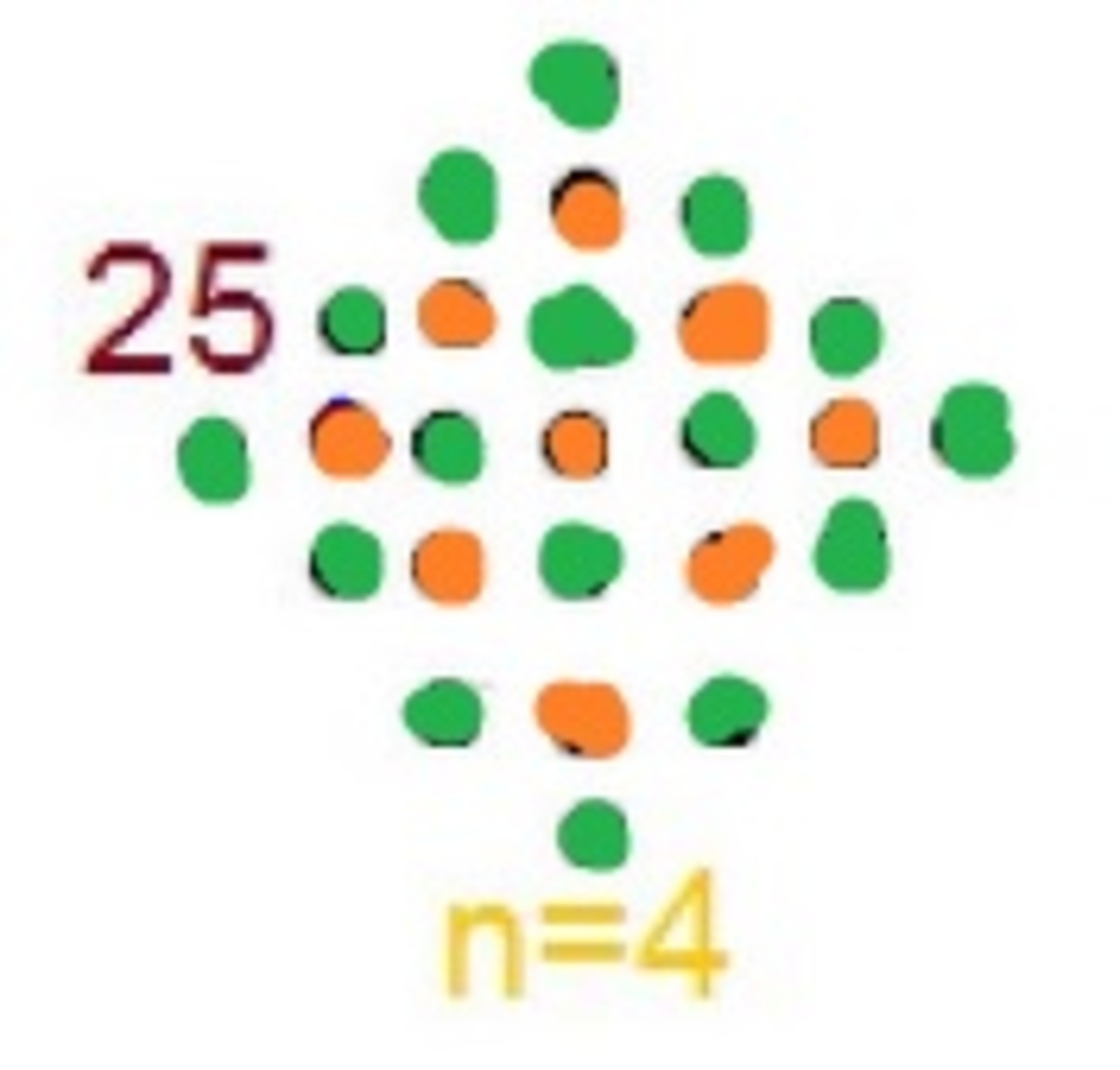
No. of orange dots= ( n − 1 ) 2 No. of green dots= n 2
Total no. of dots= ( n − 1 ) 2 + n 2
Putting n = 1 0 1 0 3
We can observe a pattern while finding the sum of digits of numbers in the form ( 1 0 a ) 2 + ( 1 0 a − 1 ) 2
( 1 0 1 ) 2 + ( 1 0 1 − 1 ) 2 = 1 8 1 , sum of digits=10.
( 1 0 2 ) 2 + ( 1 0 2 − 1 ) 2 = 1 9 8 0 1 , sum of digits=19
( 1 0 3 ) 2 + ( 1 0 3 − 1 ) 2 = 1 9 9 8 0 0 1 , sum of digits=28
( 1 0 4 ) 2 + ( 1 0 4 − 1 ) 2 = 1 9 9 9 8 0 0 0 1 , sum of digits=37
So this forms an AP with initial term 1 + 9 and common difference of 9 .
So we can observe that for numbers in the form ( 1 0 a ) 2 + ( 1 0 a − 1 ) 2 , sum of digits is 1 + 9 a
So for n = 1 0 1 0 3 , the sum of digits is 1 + 9 × 1 0 3 which is equal to 9 0 0 1
Moderator note:
You need to show that that the sum of digits is in the form of 1 + 9 a .
The difference between consecutive terms are in AP. The general term can be written as
T
n
=
1
+
4
(
1
+
2
+
.
.
.
+
(
n
−
1
)
)
=
1
+
2
n
(
n
−
1
)
For
n
=
1
0
r
,
T
n
=
1
+
2
×
1
0
r
×
(
1
0
r
−
1
)
.
1 0 r − 1 has r consecutive 9 's in it. Multiplying it by two will give us a number of the form 1 9 9 9 . . . 9 9 9 8 with r − 1 consecutive 9 's in it. Multiplying it by 1 0 r will add r zeroes to the number and the sum of digits will be 9 r Finally, we add the 1 and the sum of digits will be 9 r + 1 = 9 × 1 0 0 0 + 1 = 9 0 0 1 .
First we should say that 1 0 1 0 3 = 1 0 1 0 0 0 .
So the change in the number of dots increases by 4 each term, so dividing that by 2 will gives us a = 2 . Next, since we know the rate of increase of change is 4 , when x = 0 , y = 1 . So we have y = 2 x 2 + b x + 1 . Replacing the x and y values... we find that b = − 2 . We now have our quadratic equation y = 2 x 2 − 2 x + 1 .
When we have x = 1 0 1 0 0 0 , the sum of digits of 2 x 2 is 2 + 0 × 2 0 0 0 . Now when we subtract 2 x , we know that there are 1 0 0 0 digits, in 2 × 1 0 1 0 0 0 , and the first (from the right) 9 9 9 are zeroes. However, the first non-zero digit is the thousandth digit, and it is 8 (since we are subtracting 2 from 1 0 ). Since that would leave a 1 , all the other digits (excepting the first from the left) would be 9 ( 9 + 1 = 1 0 ). The first digit must be less than 2 , but greater than 0 , so it is 1 . So now we have the sum of digits is 1 + 9 × 9 9 9 + 8 . Finally, we have + 1 , so our sum of digits is now
1 + 9 × 9 9 9 + 9 = 1 + 9 × 1 0 0 0 = 9 0 0 1 .
We note that the tilted square of dots is equal to two triangle less a diagonal of dots. The number of dots on the diagonal = 2 n − 1 .
The number of dots on the n t h term is D ( n ) = 2 ( 2 n ( 1 + 2 n − 1 ) ) − ( 2 n − 1 ) = 2 n 2 − 2 n + 1
Therefore,
D ( 1 0 1 0 3 ) = D ( 1 0 1 0 0 0 ) = 2 × 1 0 2 0 0 0 − 2 × 1 0 1 0 0 0 + 1 = 2 × 1 0 2 0 0 0 − 1 0 1 0 0 1 + 1 0 1 0 0 1 − 2 × 1 0 1 0 0 0 + 1 = ( 2 × 1 0 2 0 0 0 − 1 0 1 0 0 1 ) + 8 × 1 0 1 0 0 0 + 1 = ( 2 × 1 0 9 9 9 − 1 ) 1 0 1 0 0 1 + 8 × 1 0 1 0 0 0 + 1 = 1 followed by 999 × 9 followed by 8 followed by 999 × 0 followed by 1
Therefore, the sum of digits of D ( 1 0 1 0 0 0 ) is:
N = 1 + 9 9 9 × 9 + 8 + 0 + 1 = 9 0 0 1