Tilted Triangles
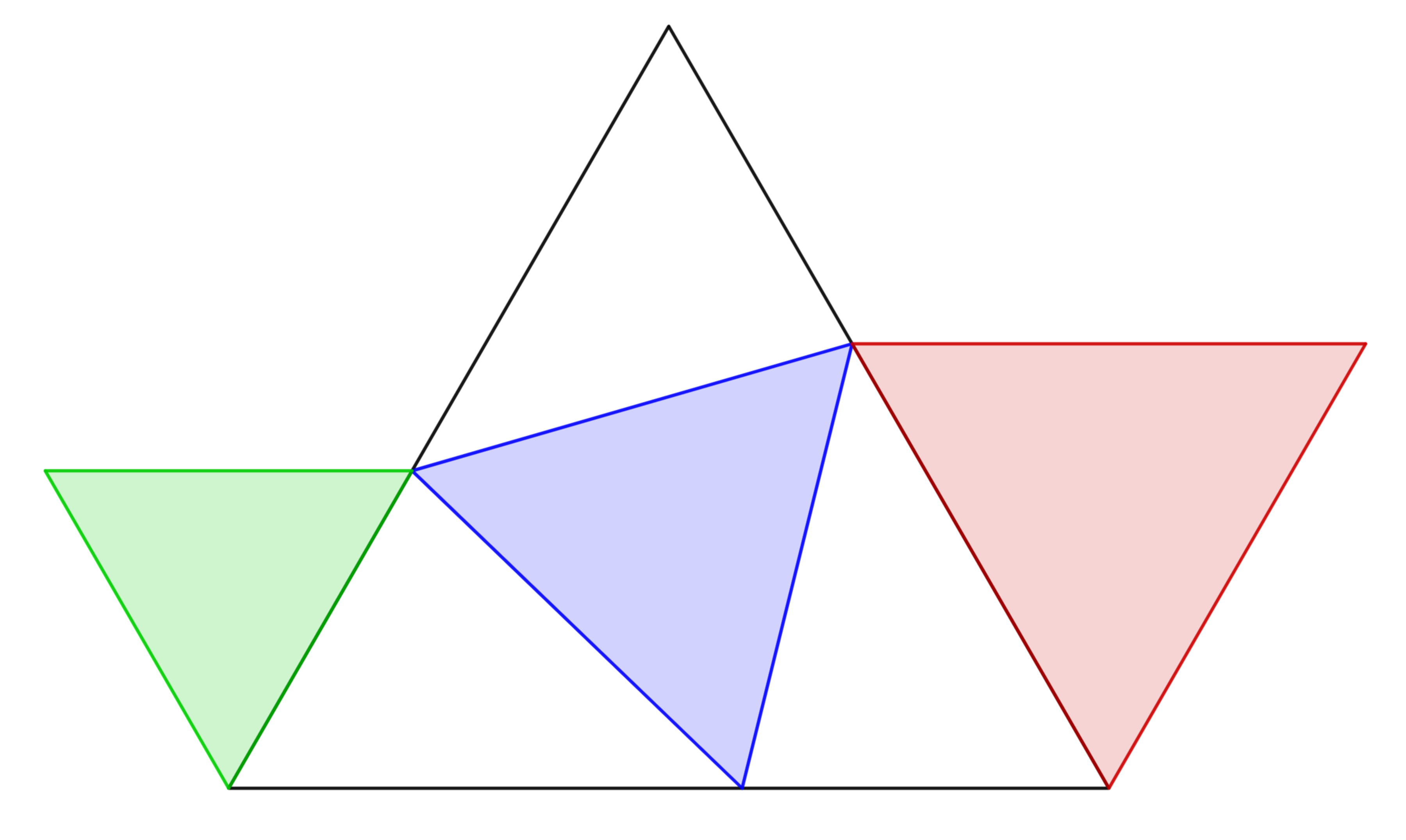
There are four equilateral triangles in the image. If the area of the red triangle is 98 and the area of the green triangle is 50, what is the area of the blue triangle?
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
It's hard to be original. :)

The ratio of side lengths of the red and green equilateral triangles is 5 0 9 8 = 5 7 . Let the side lengths of the red and green equilateral triangles be 7 k and 5 k respectively, and the side length of the blue equilateral triangle be a . Let angle between the right side of the blue triangle and the horizontal line be θ . Then the angle between the left side of the blue triangle with the horizontal line is 1 2 0 ∘ − θ . By sine rule , we have: 7 k sin θ = a sin 6 0 ∘ and 5 k sin ( 1 2 0 ∘ − θ ) = a sin 6 0 ∘ . Then
7 k sin θ 7 sin θ 5 sin θ 3 sin θ tan θ ⟹ sin θ = 5 k sin ( 1 2 0 ∘ − θ ) = 5 2 3 cos θ + 2 1 sin θ = 2 7 3 cos θ + 2 7 sin θ = 7 3 cos θ = 3 7 = 2 1 3 7
By sine rule again:
sin 6 0 ∘ a 3 2 a ⟹ a = sin θ 7 k = 7 7 k ⋅ 2 1 3 = 3 9 k
Since the area of similar triangle is directly proportional to the square of the side length, the area of the blue equilateral triangle is 4 9 k 2 3 9 k 2 ⋅ 9 8 = 7 8 .
Red area = 2 x 7² = 98
Green area = 2 x 5² = 50
White + blue area
= 2 x (5 + 7)² = 288
1 White area = 2 x 5 x 7 = 70
Blue area
= {White + blue area} - 3 x {white area}
= 288 - 3 x 70
= 288 - 210
= 78
This problem is similar to this problem .
The three white triangles all have angles that are 6 0 ° , θ , and 1 2 0 ° − θ and one side congruent to the side of the blue equilateral triangle, so they are all congruent by the ASA congruency theorem.
Let A and a be the area and side of the green equilateral triangle, B and b be the area and side of the red equilateral triangle, C be the area of the blue equilateral triangle, D be the area of each of the white triangles, and E be the area of the large equilateral triangle. The sides of E are then a + b , and E = C + 3 D .
By triangle area equations,
A = 4 3 a 2
B = 4 3 b 2
D = 2 1 a b sin 6 0 ° = 4 3 a b = A B
E = 4 3 ( a + b ) 2 = 4 3 a 2 + 2 4 3 a b + 4 3 b 2 = A + 2 D + B = A + B + 2 A B
C = E − 3 D = ( A + B + 2 A B ) − 3 A B = A + B − A B
In this question, A = 5 0 and B = 9 8 , so C = 5 0 + 9 8 − 5 0 ⋅ 9 8 = 7 8 .