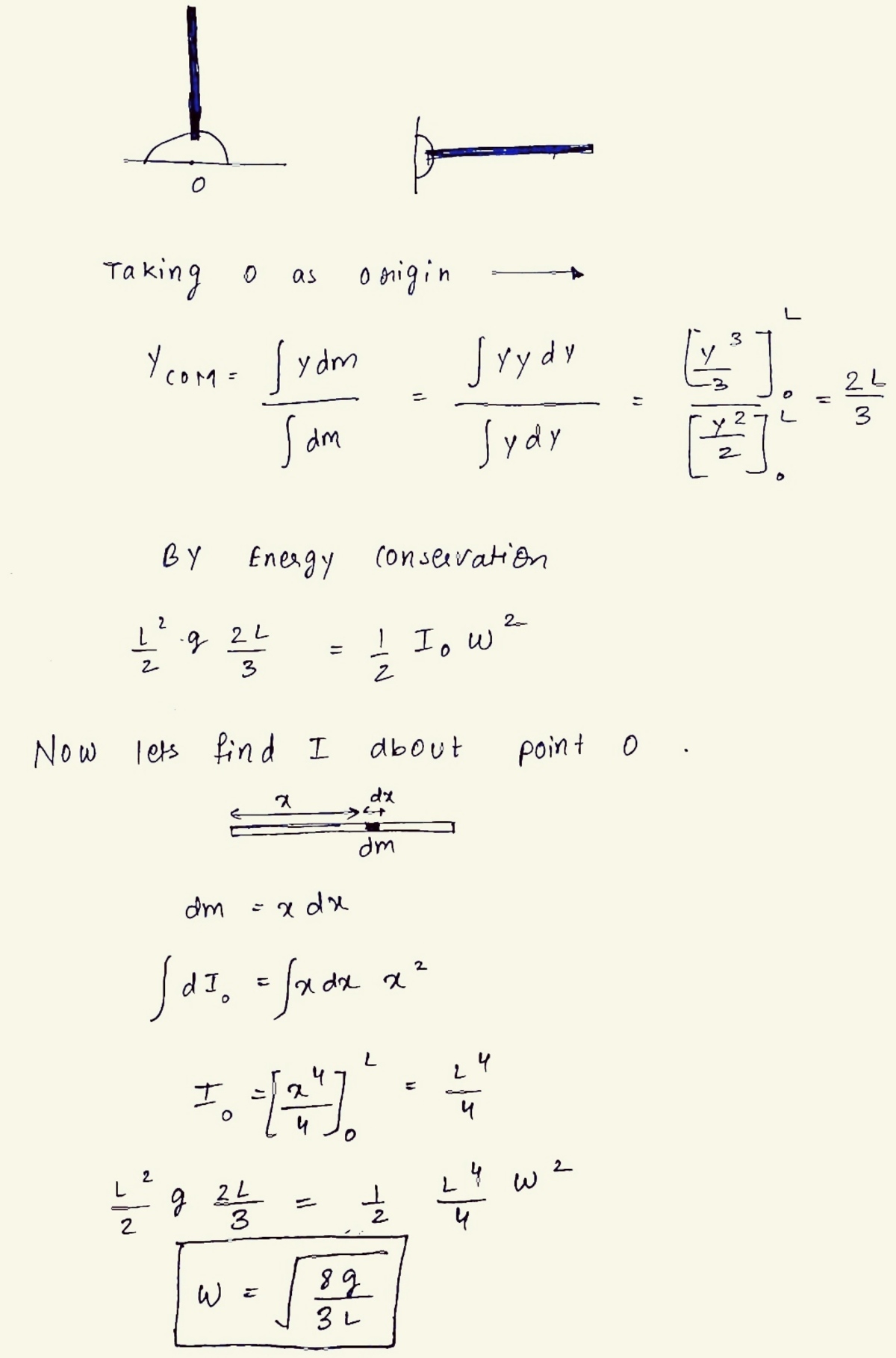Tilting Rod
There is a non-uniform straight rod of length L , aligned with the y (vertical) axis. One end of the rod is hinged at the origin. The linear mass density of the rod at a particular point is equal to the y position along the rod ( 0 ≤ y ≤ L ) . The ambient gravitational acceleration g is in the − y direction.
Starting from rest in the vertical position, the rod rotates toward the horizontal axis under the influence of gravity. When the rod aligns with the horizontal axis, what is its angular speed?
Details and Assumptions:
1)
L
=
2
2)
g
=
1
0
The answer is 3.651.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Consider the rod in its vertical upright position. Treating the X-axis as the zero gravitational potential energy level, the PE of an elementary rod length d y at a distance y from the hinge is:
d V = ( λ d y ) g y
Here λ = y is the mass per unit length of the rod. Integrating the above expression from 0 to L gives:
V = 3 g L 3
Next, the moment of inertia of the rod about the hinge can be calculated as such:
I = ∫ 0 L y 2 ( λ d y ) = 4 L 4
So if the rod starts from rest from its vertically upward position and rotates till it becomes horizontal, its potential energy is converted to kinetic energy as such:
V i n i t i a l + K E i n i t i a l = V f i n a l + K E f i n a l ⟹ 3 g L 3 + 0 = 0 + 2 1 I ω 2
⟹ ω = 3 L 8 g
Mass of the rod is 2 L 2 . Moment of inertia of the rod about one of it's ends is 4 L 4 . Distance of the C.M. of the rod from the hinged end is 3 2 L . So, initial P.E. of the rod is 2 L 2 × g × 3 2 L = 3 L 3 g . Initial K.E. of the rod is zero. Final P.E. is zero and final K.E. is 2 1 × 4 L 4 × ω 2 , where ω is the required angular velocity. Applying energy conservation law, we get ω = 2 3 L 2 g . Substituting the given values of g and L we get ω ≈ 3 . 6 5 1
Awesome question.Sir keep uploading.