Time Bomb
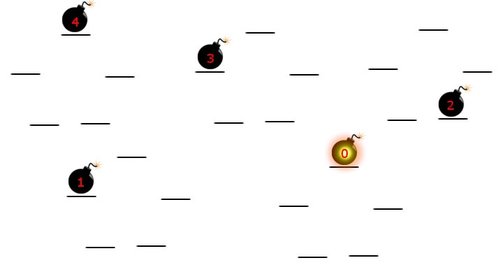 people stand in a circle. One is given a ticking bomb with
seconds left. The bomb is then thrown around the circle every second in an orderly, mathematical fashion; when the bomb has
seconds left, it is thrown to the person
places clockwise. Determine the sum of all values of
with
for which each person holds the bomb exactly once.
people stand in a circle. One is given a ticking bomb with
seconds left. The bomb is then thrown around the circle every second in an orderly, mathematical fashion; when the bomb has
seconds left, it is thrown to the person
places clockwise. Determine the sum of all values of
with
for which each person holds the bomb exactly once.
The answer is 127.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
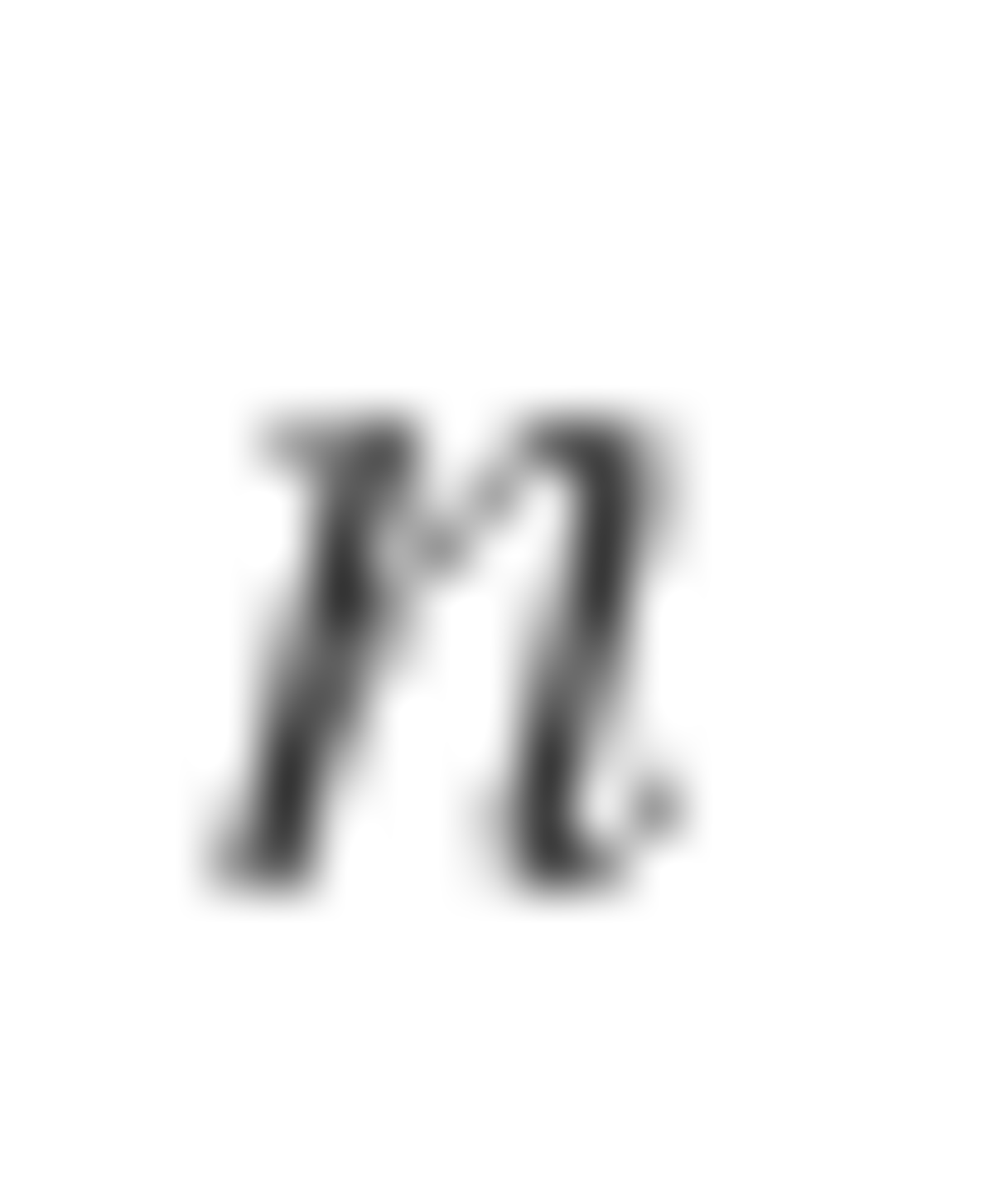
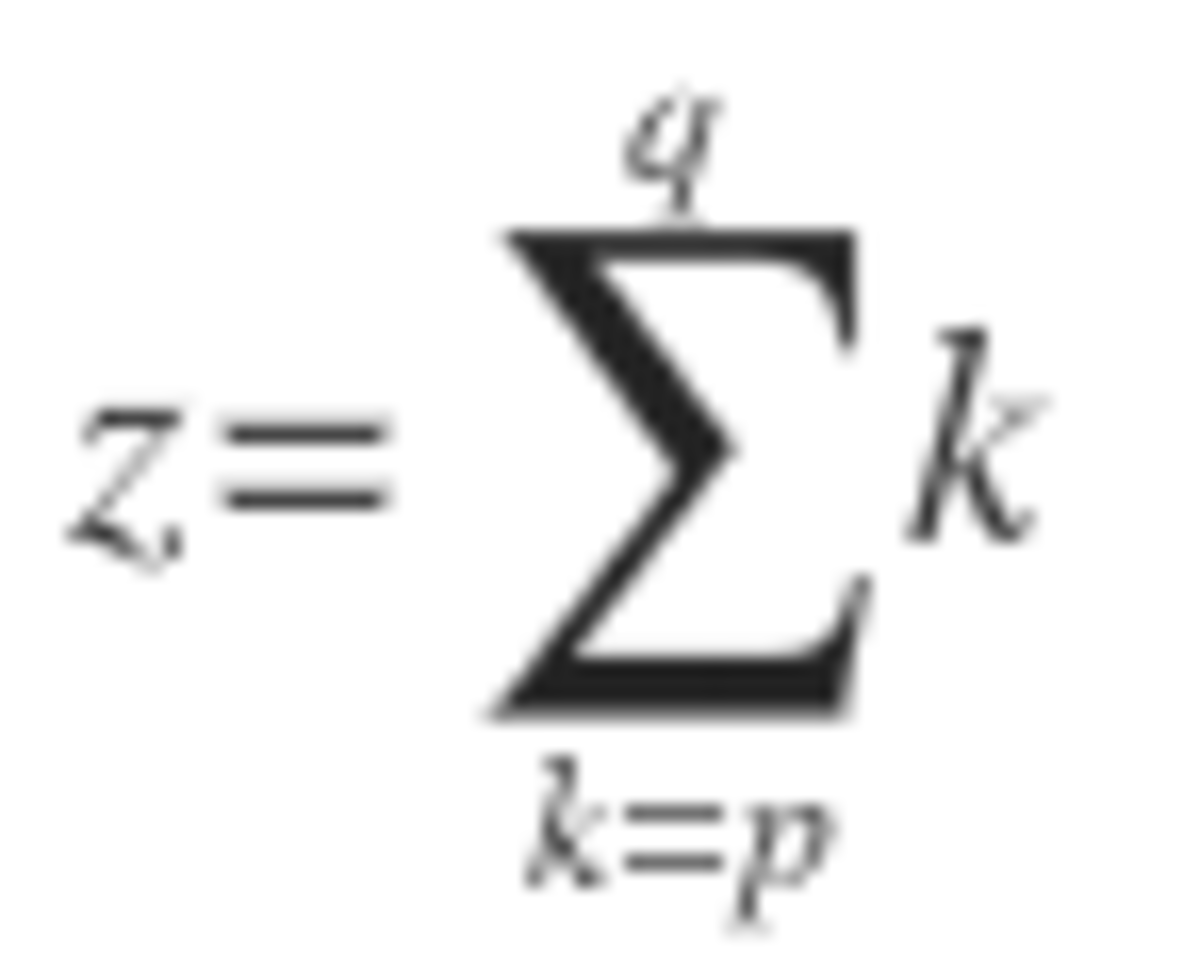
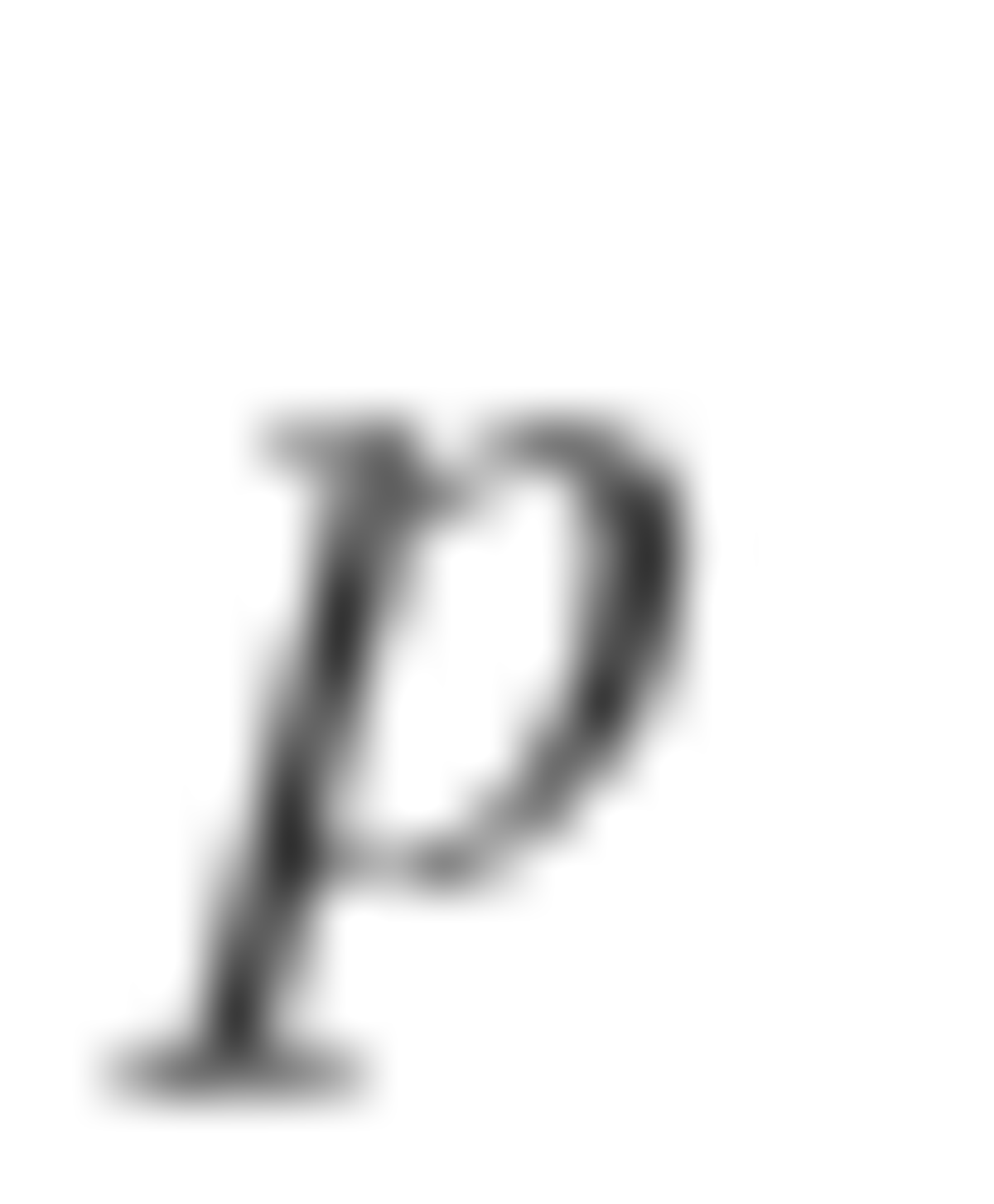
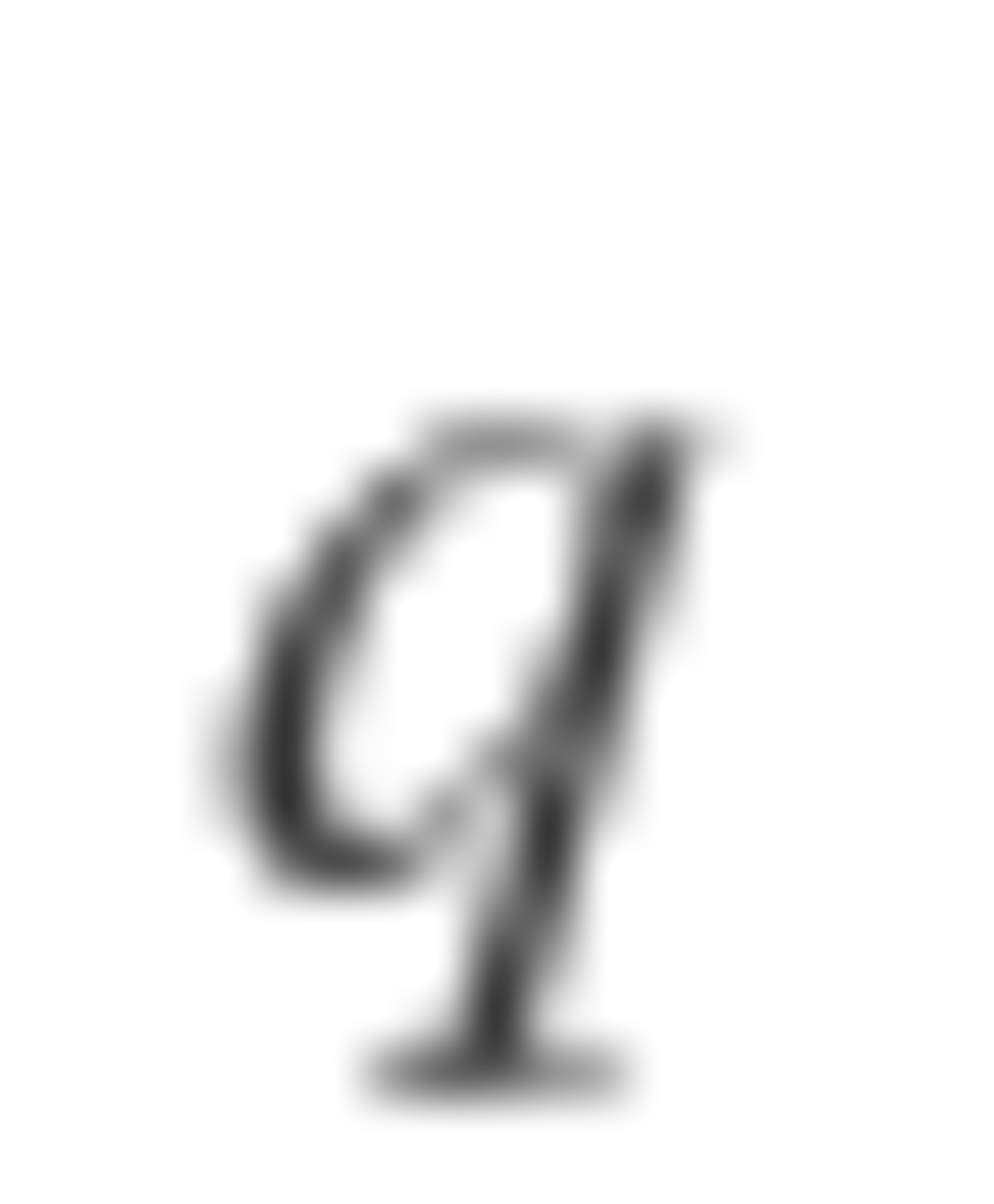
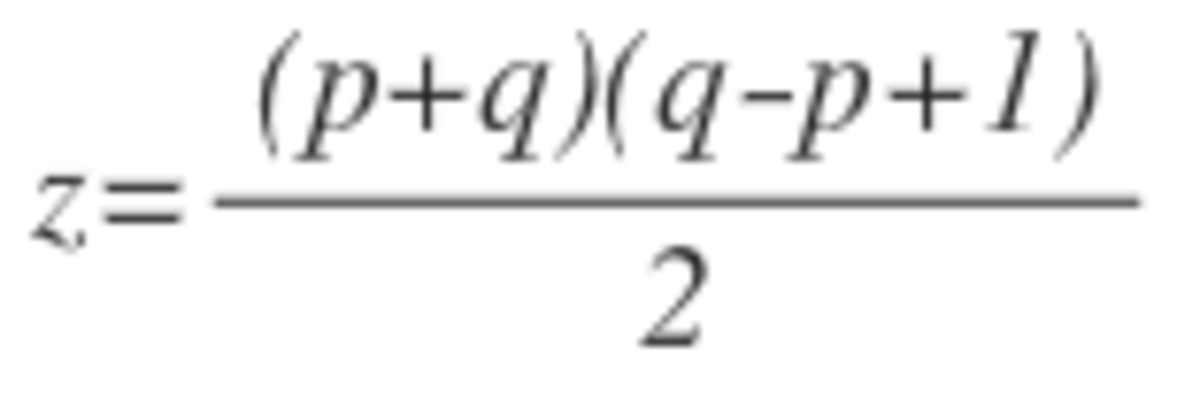
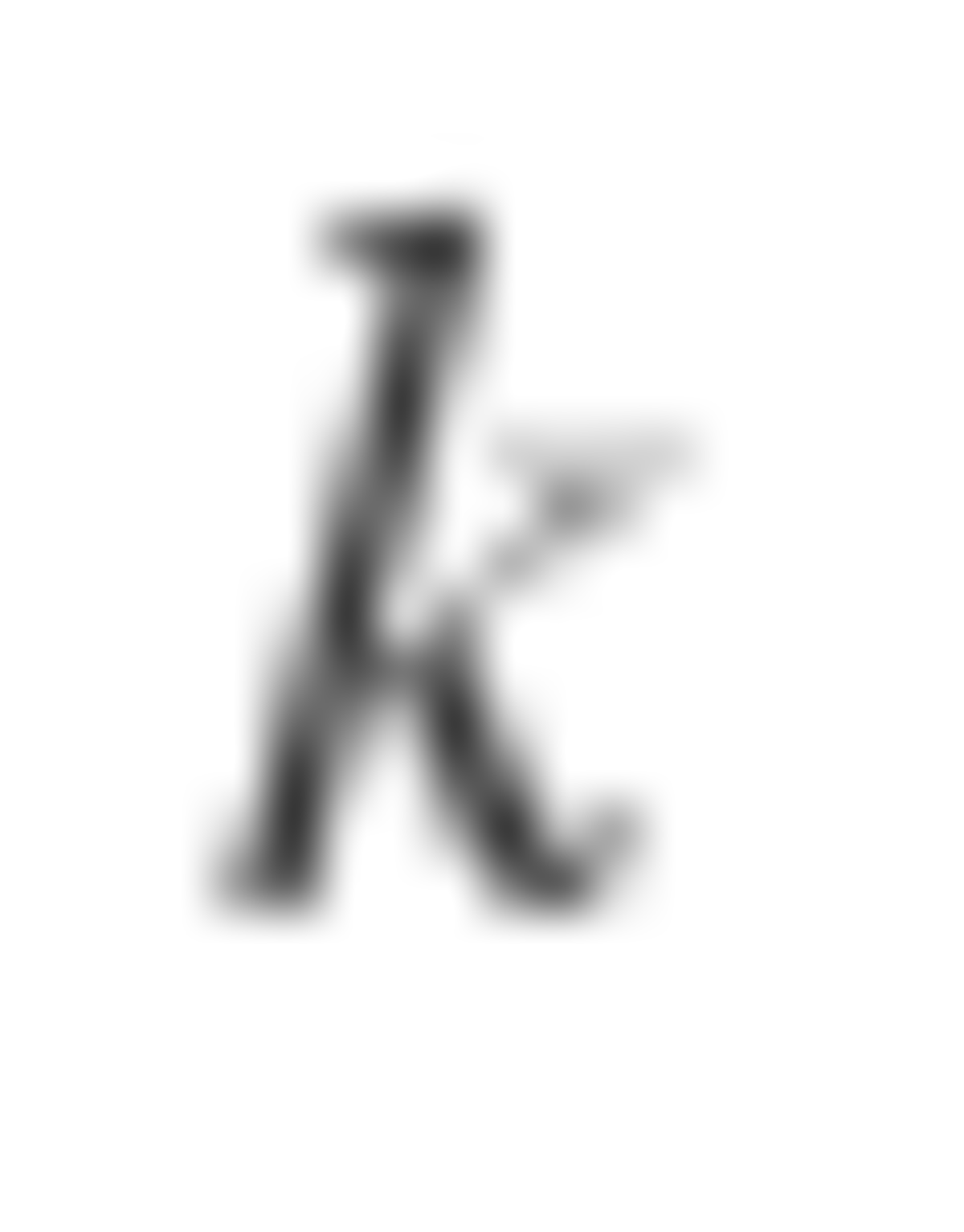
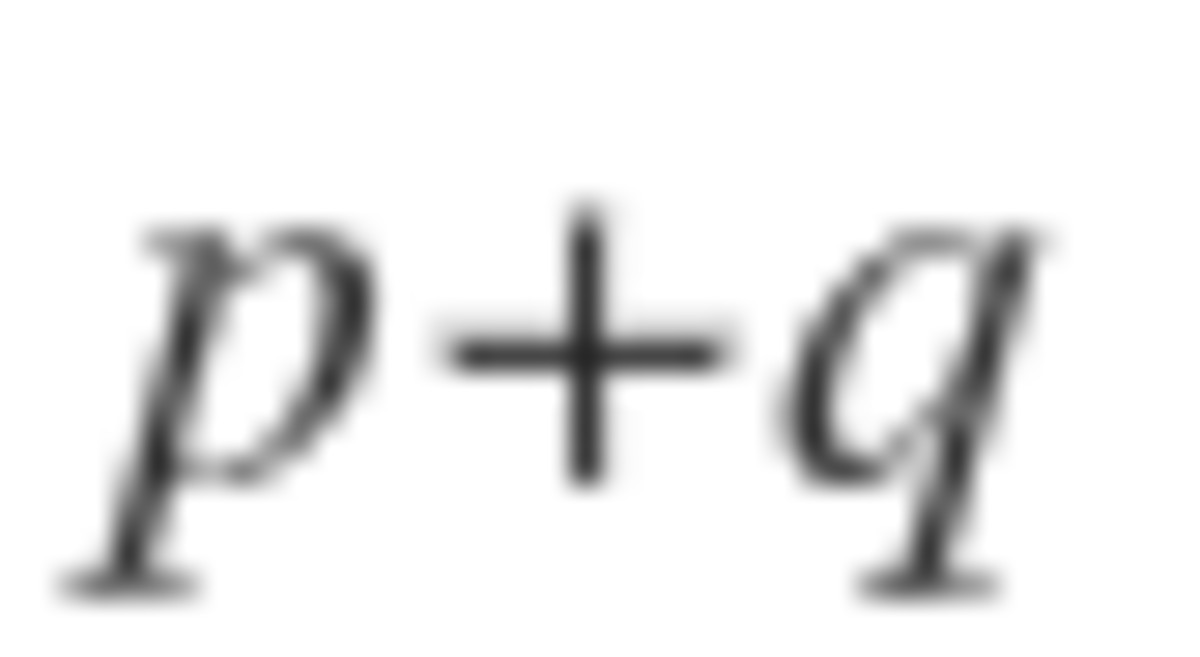
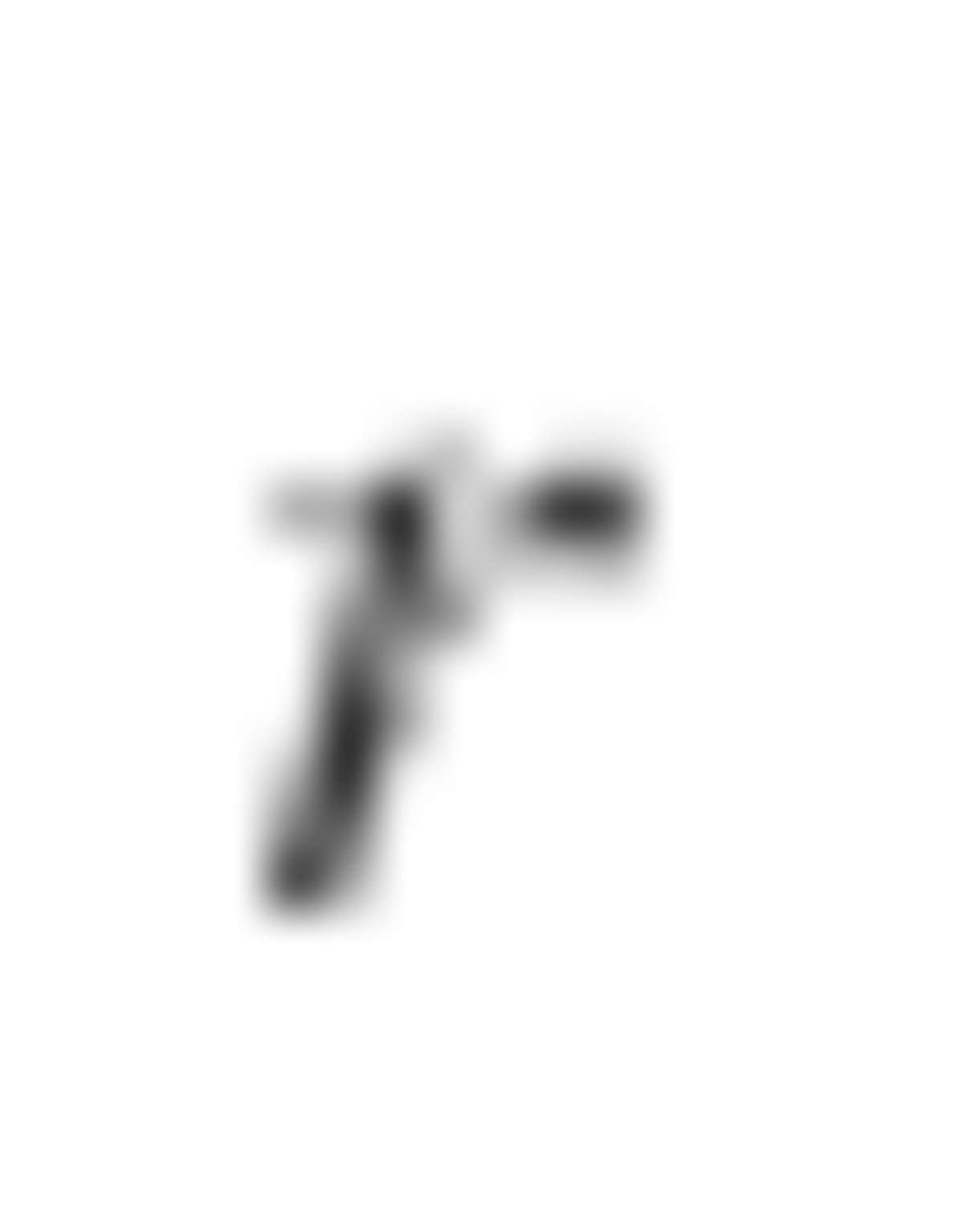
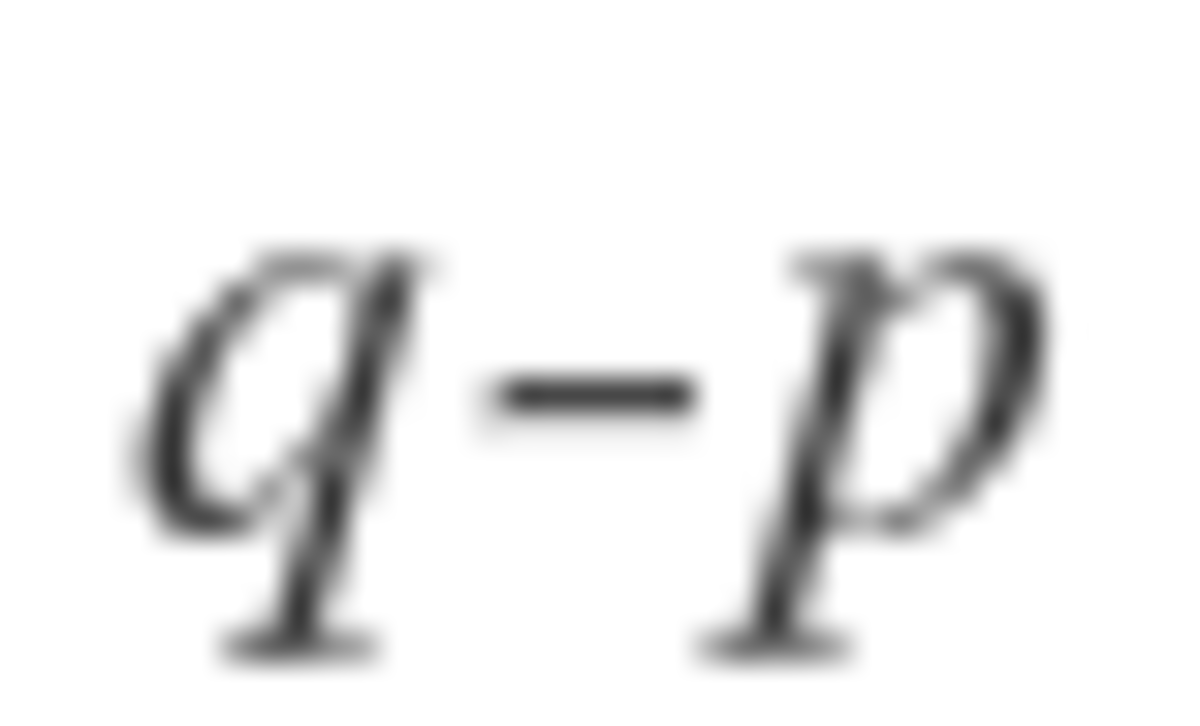
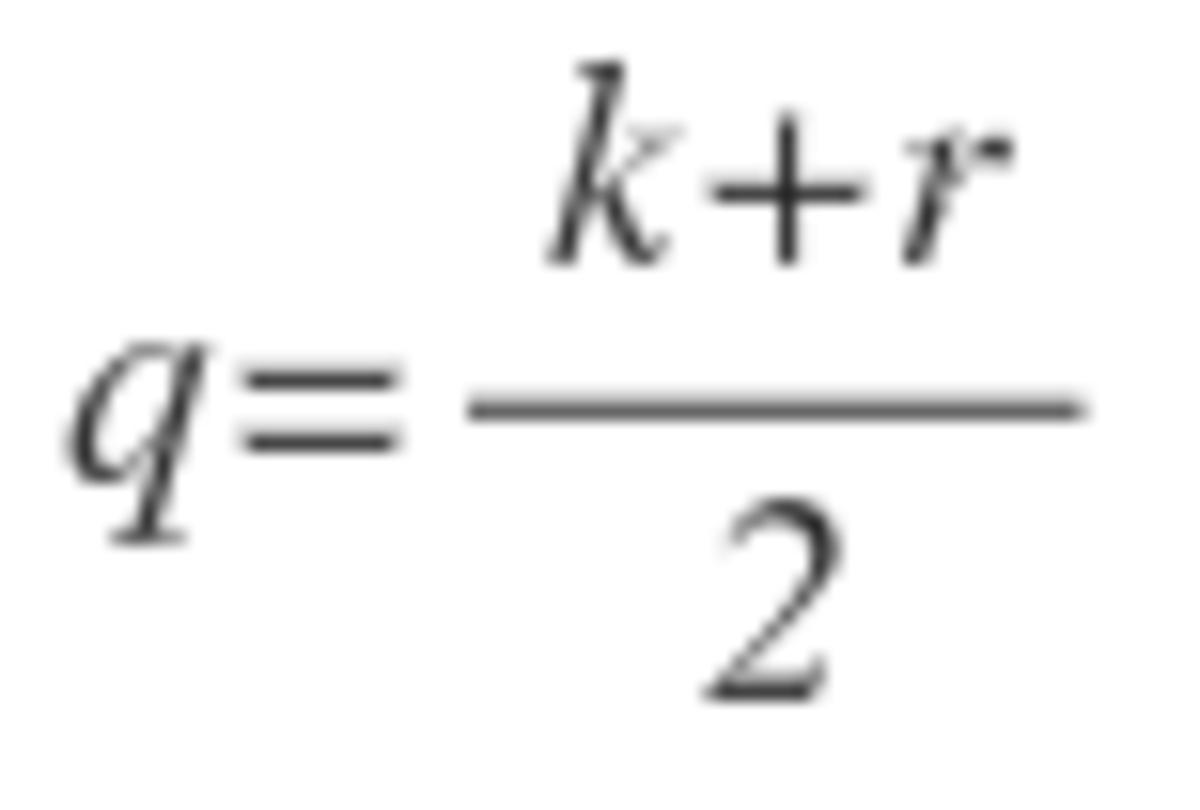
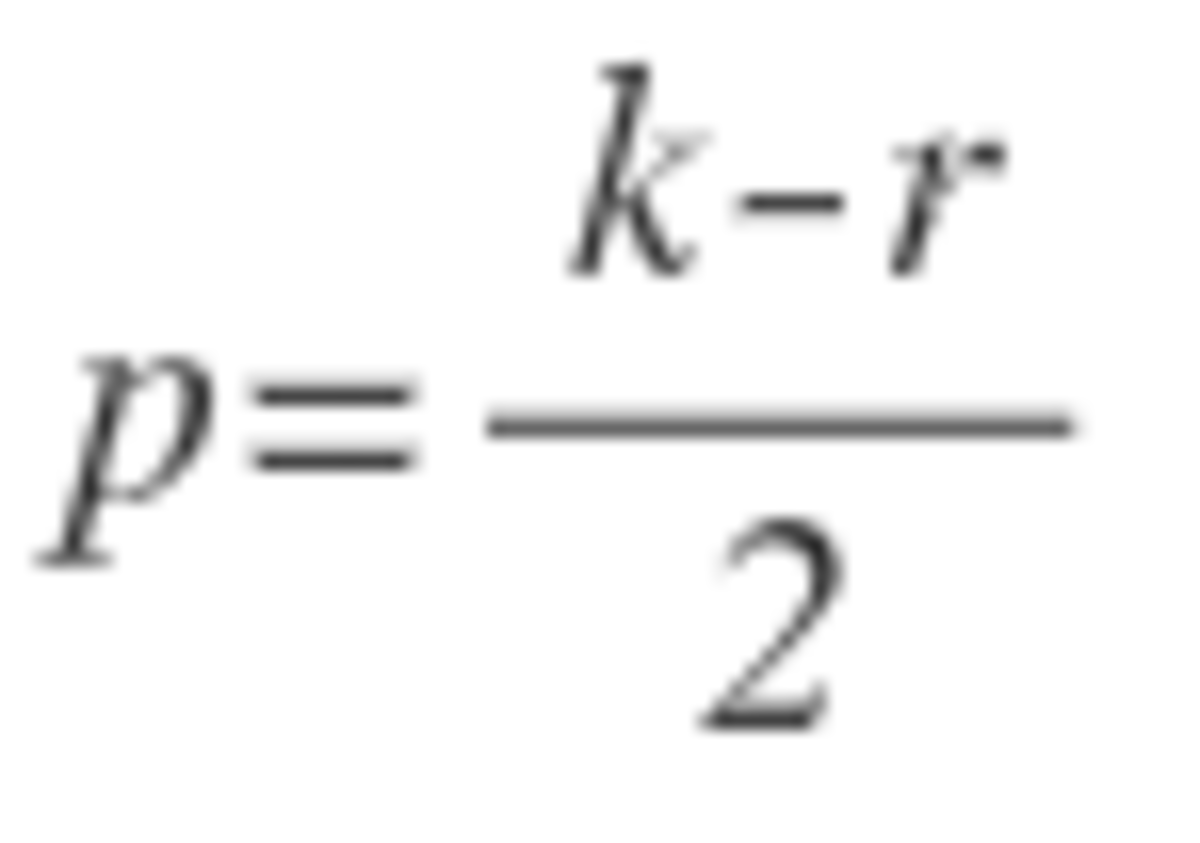
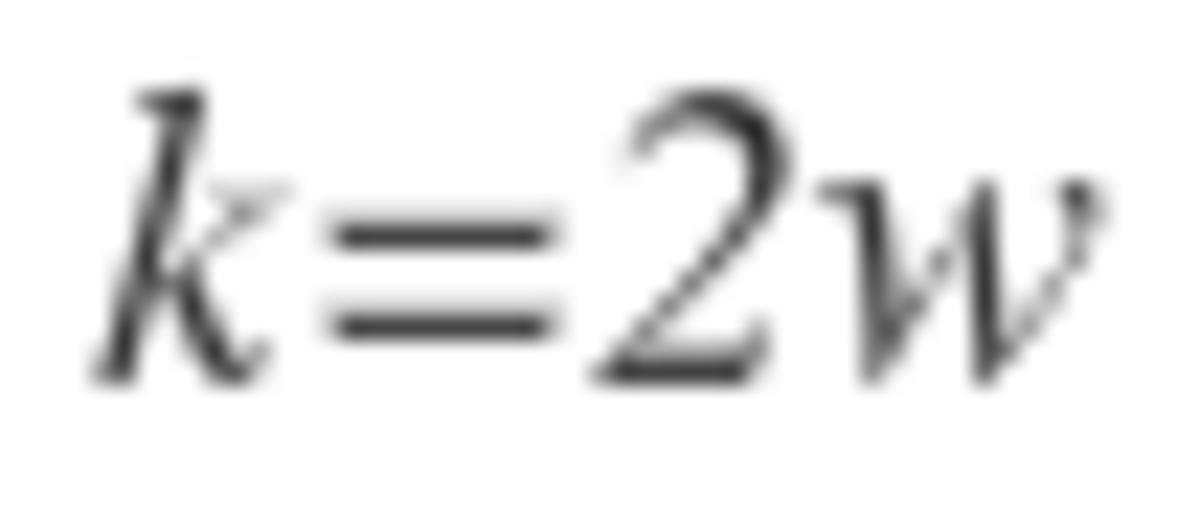
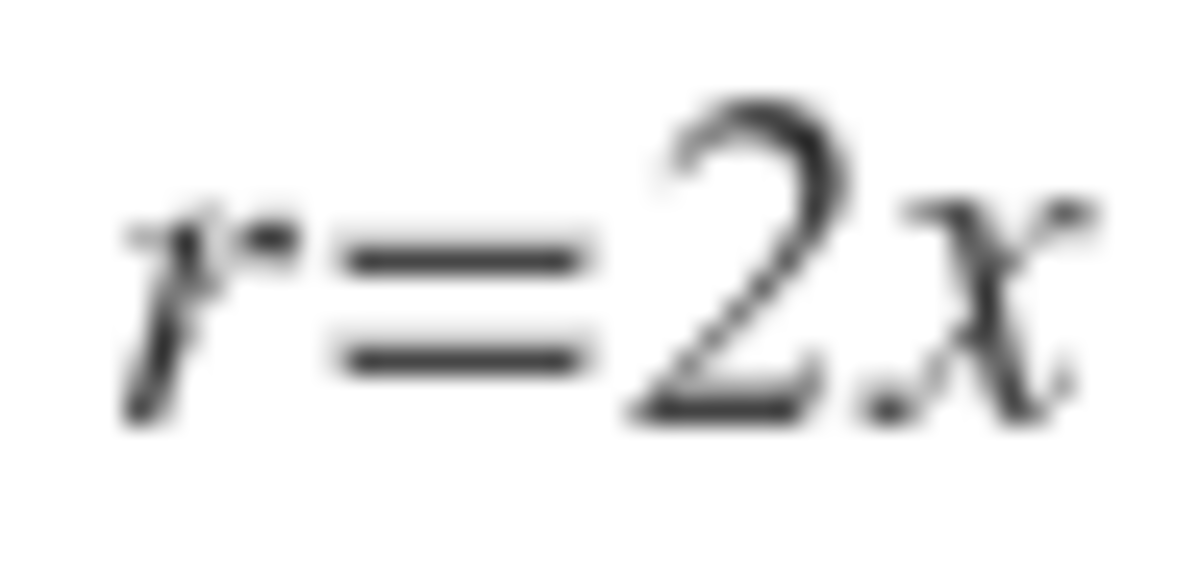
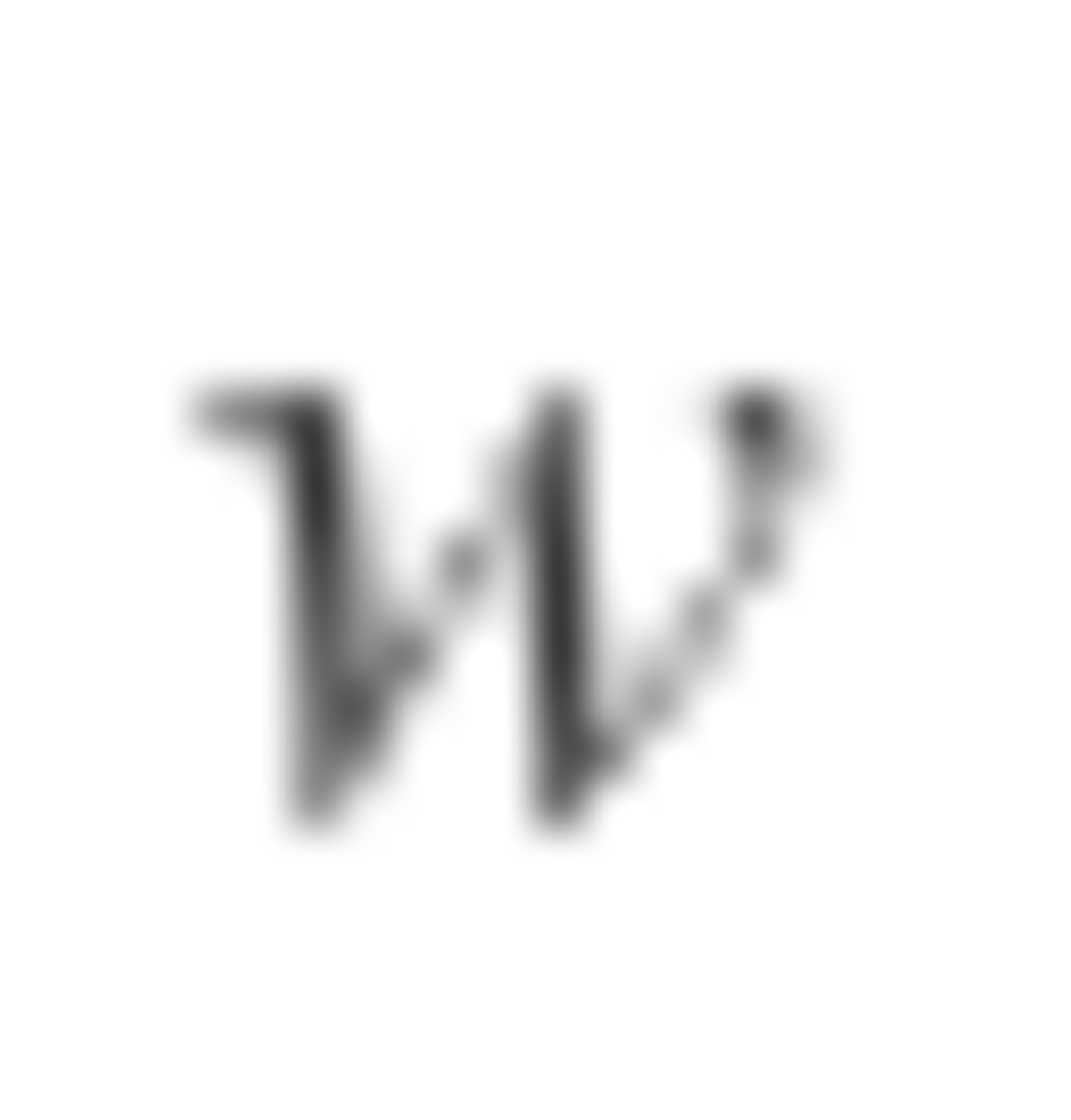
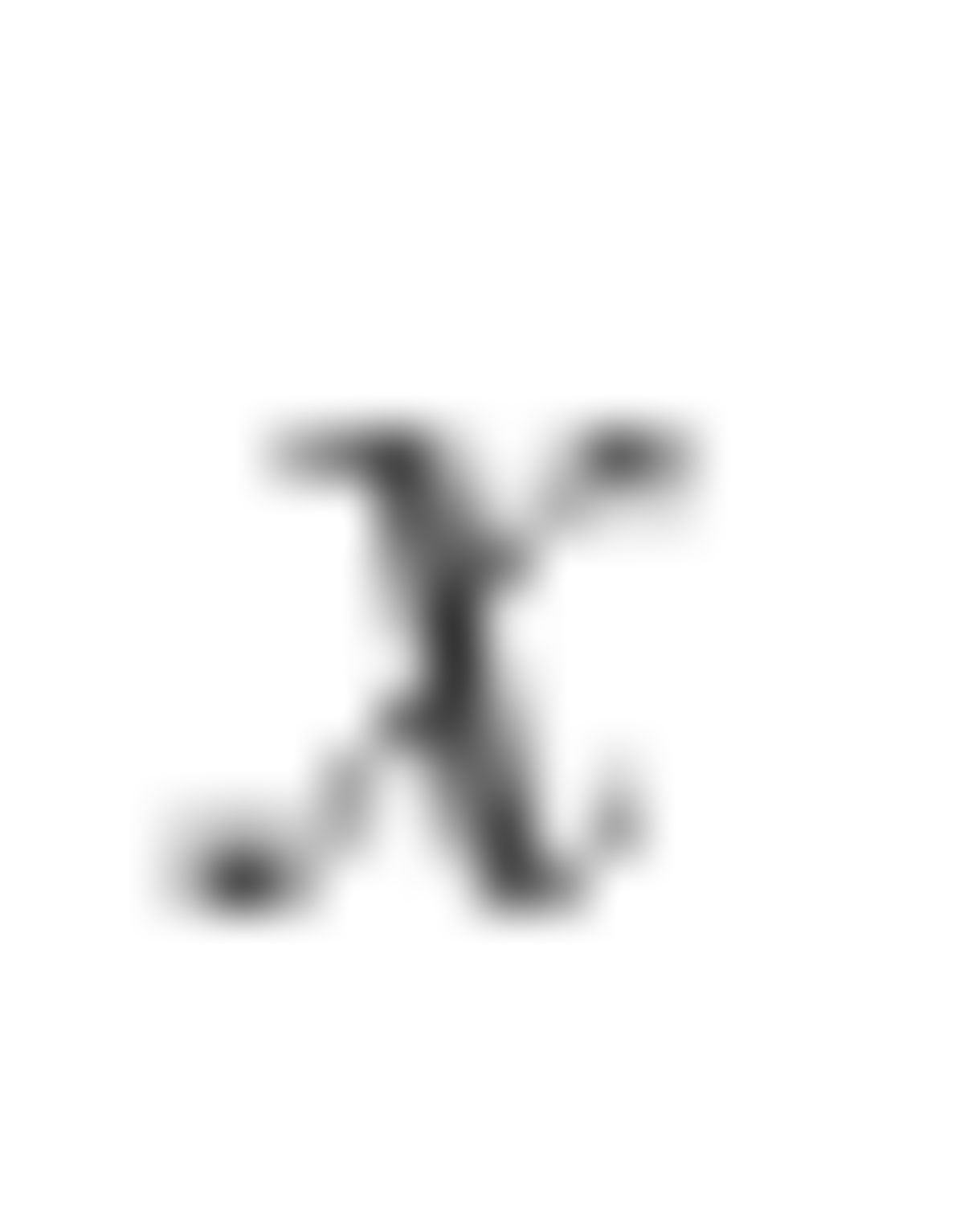
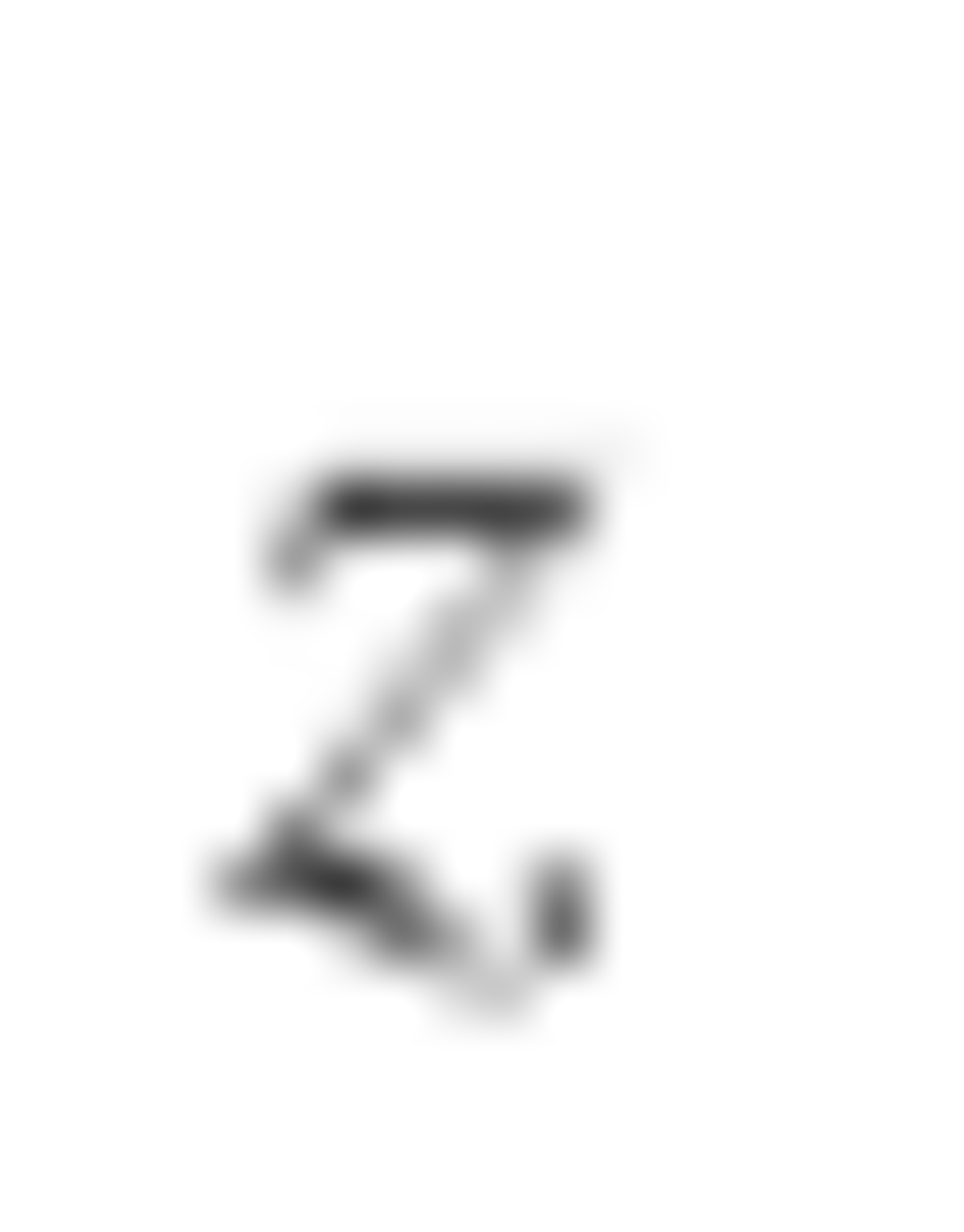
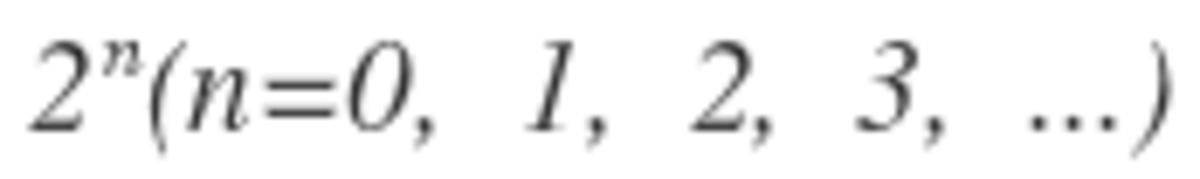
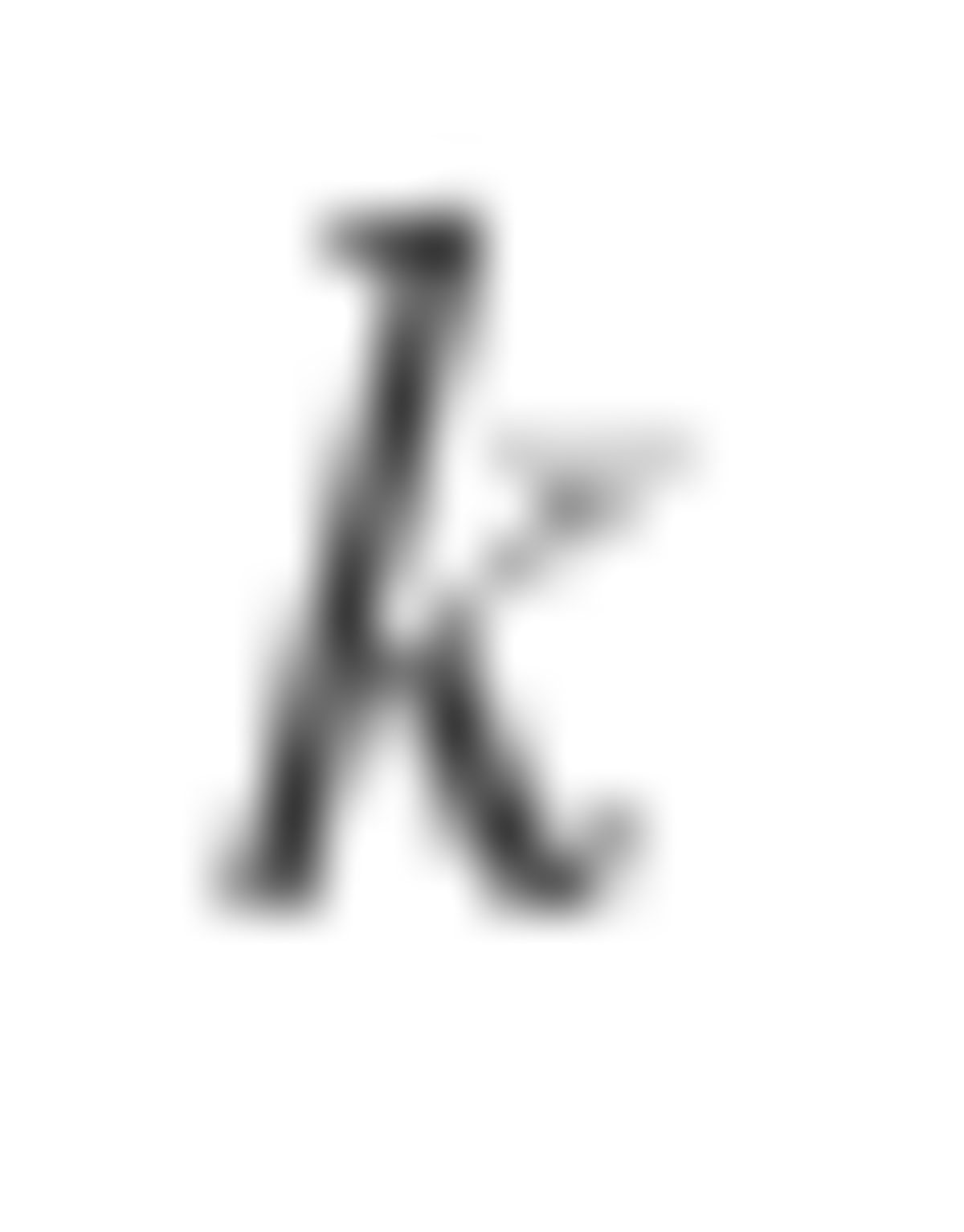
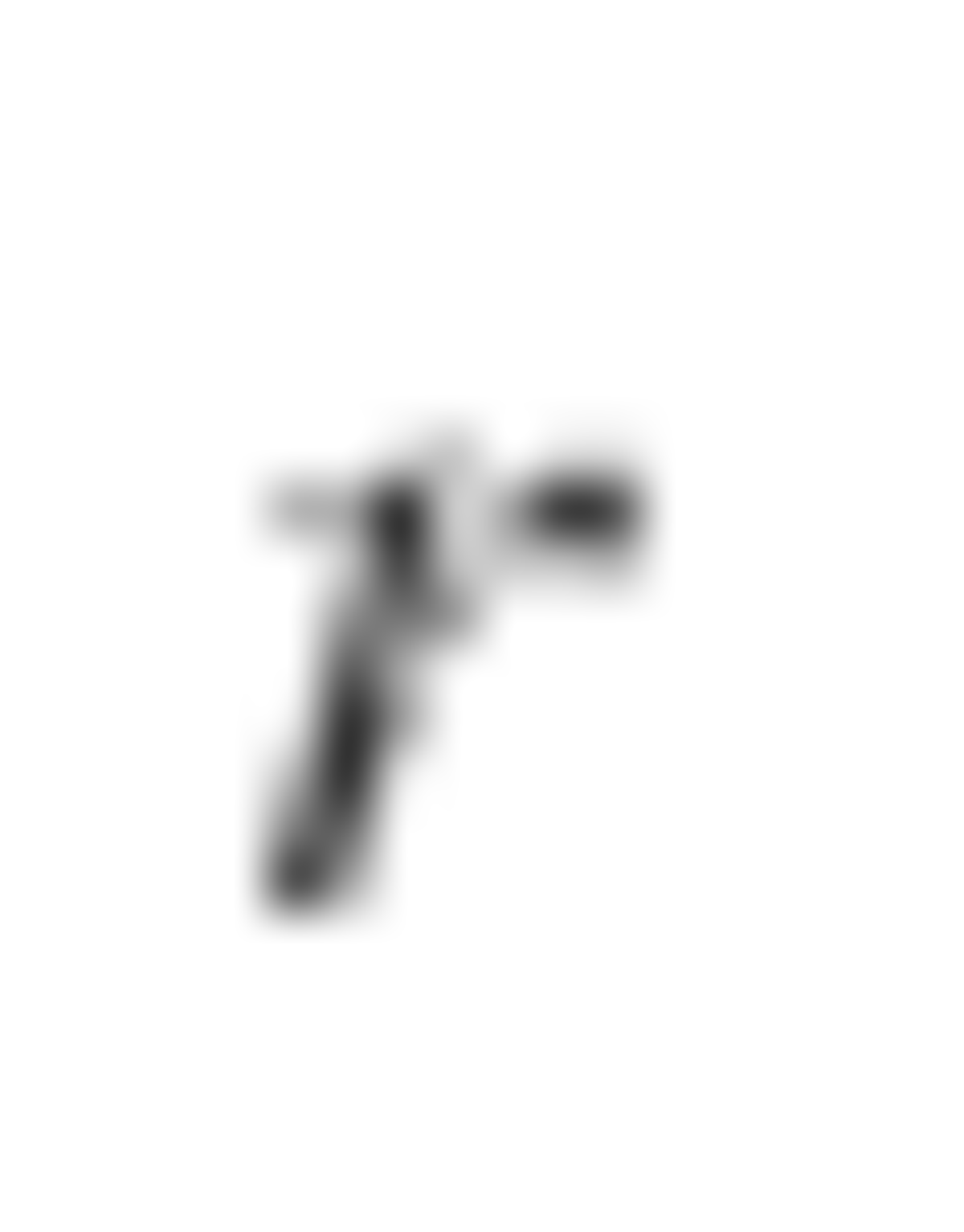
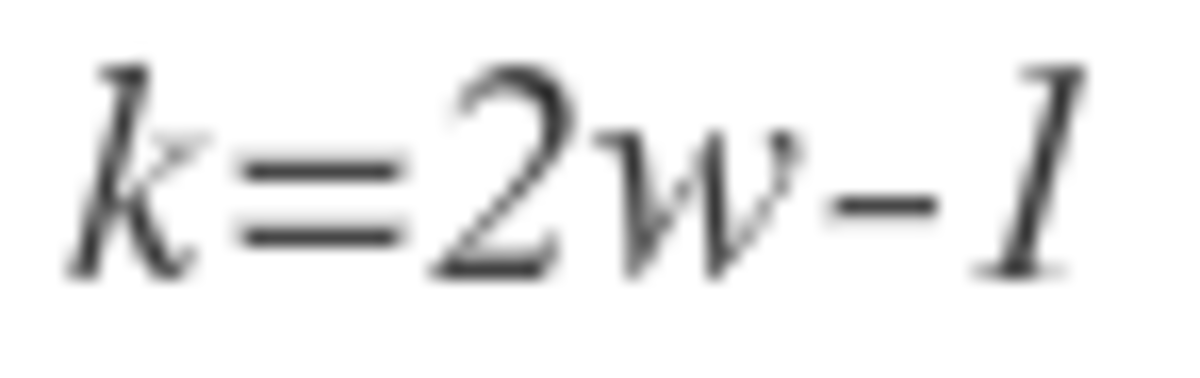
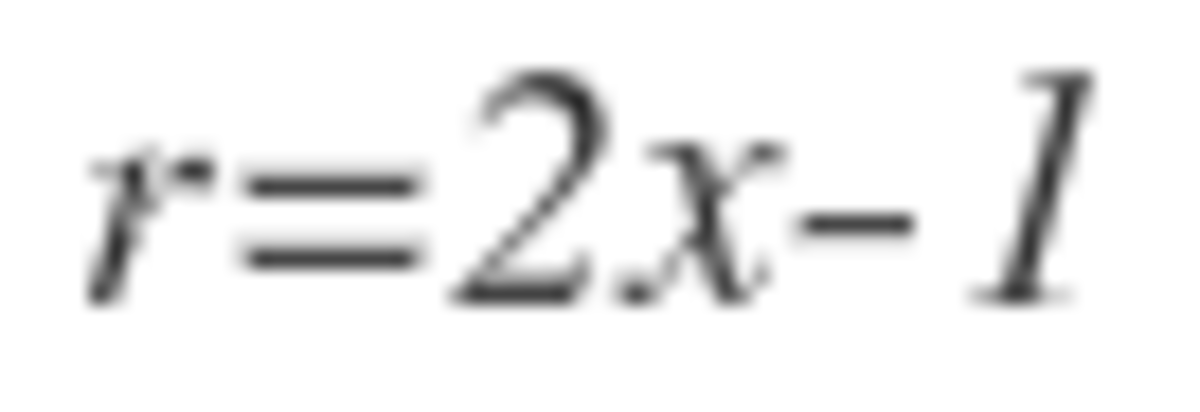
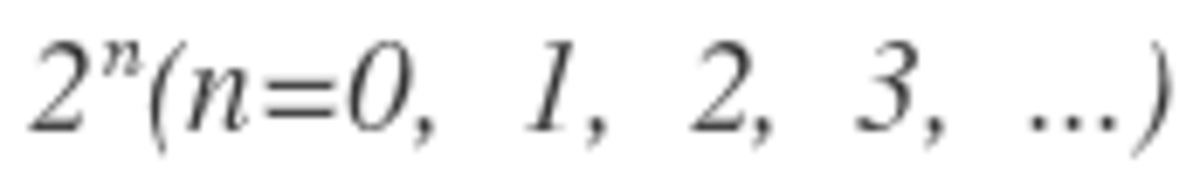
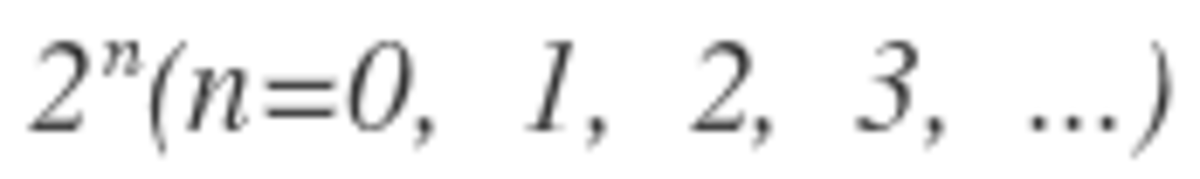
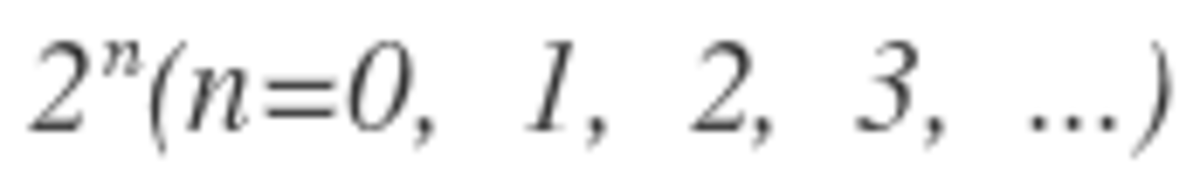
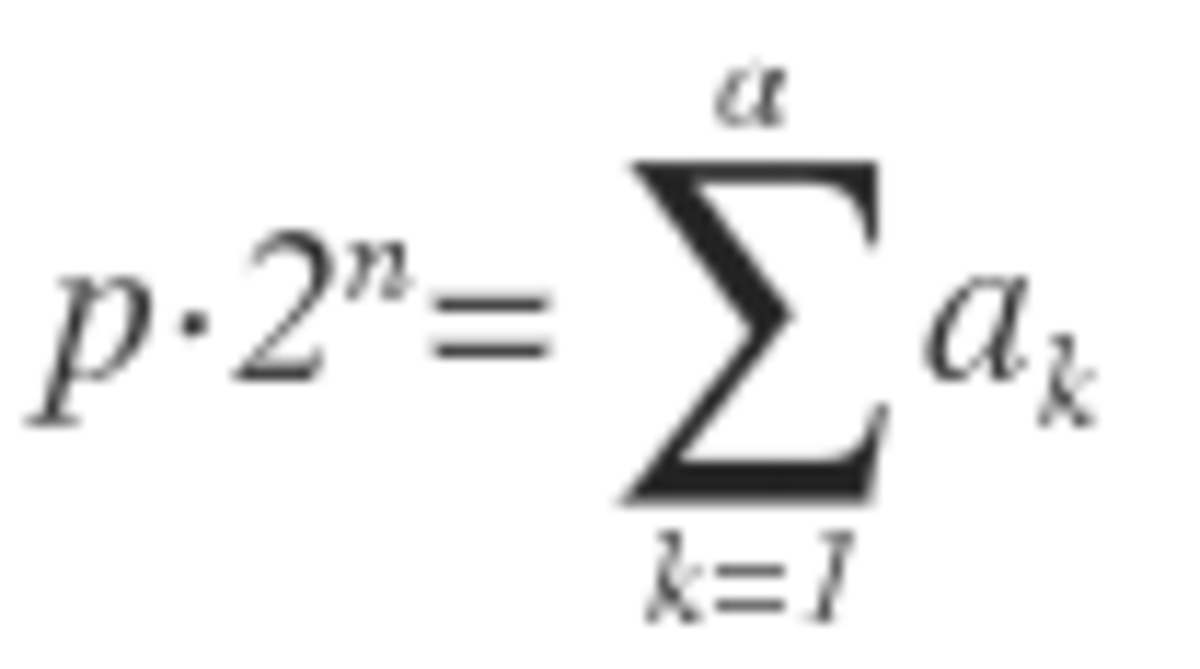
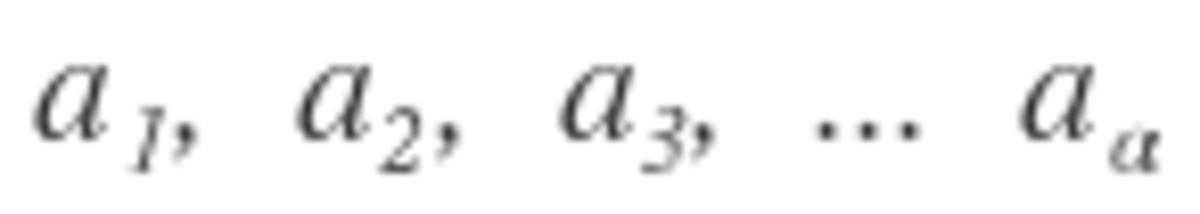
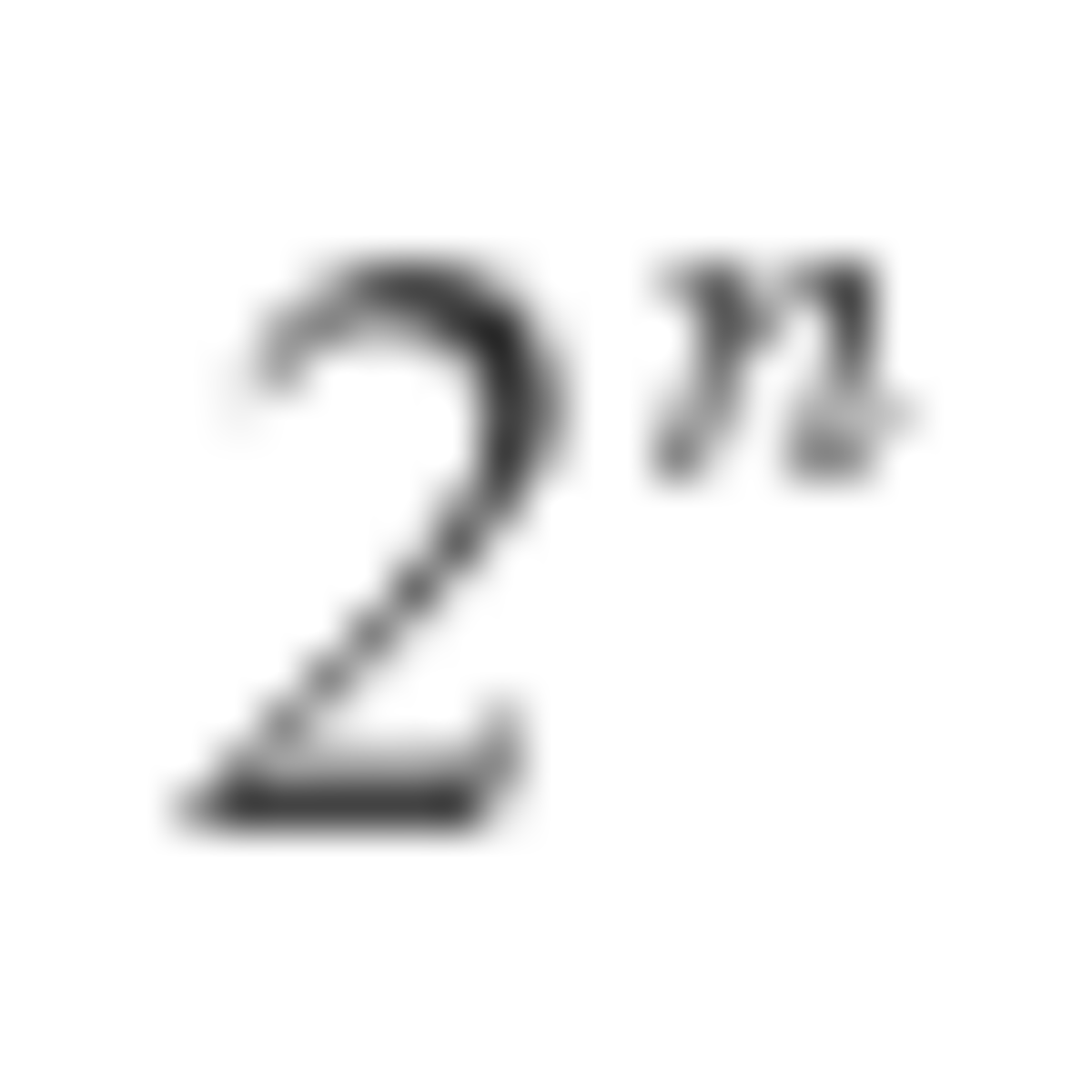
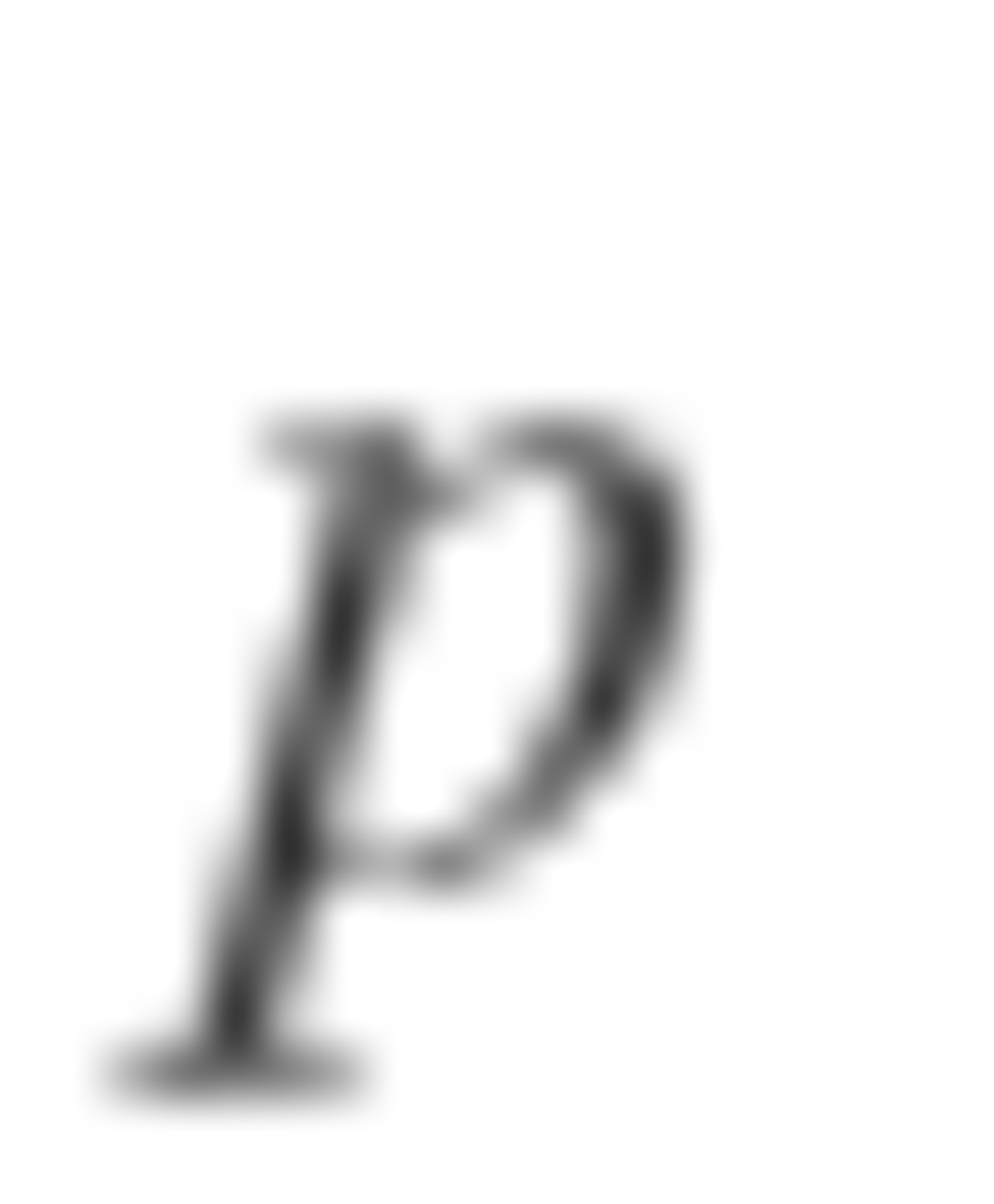
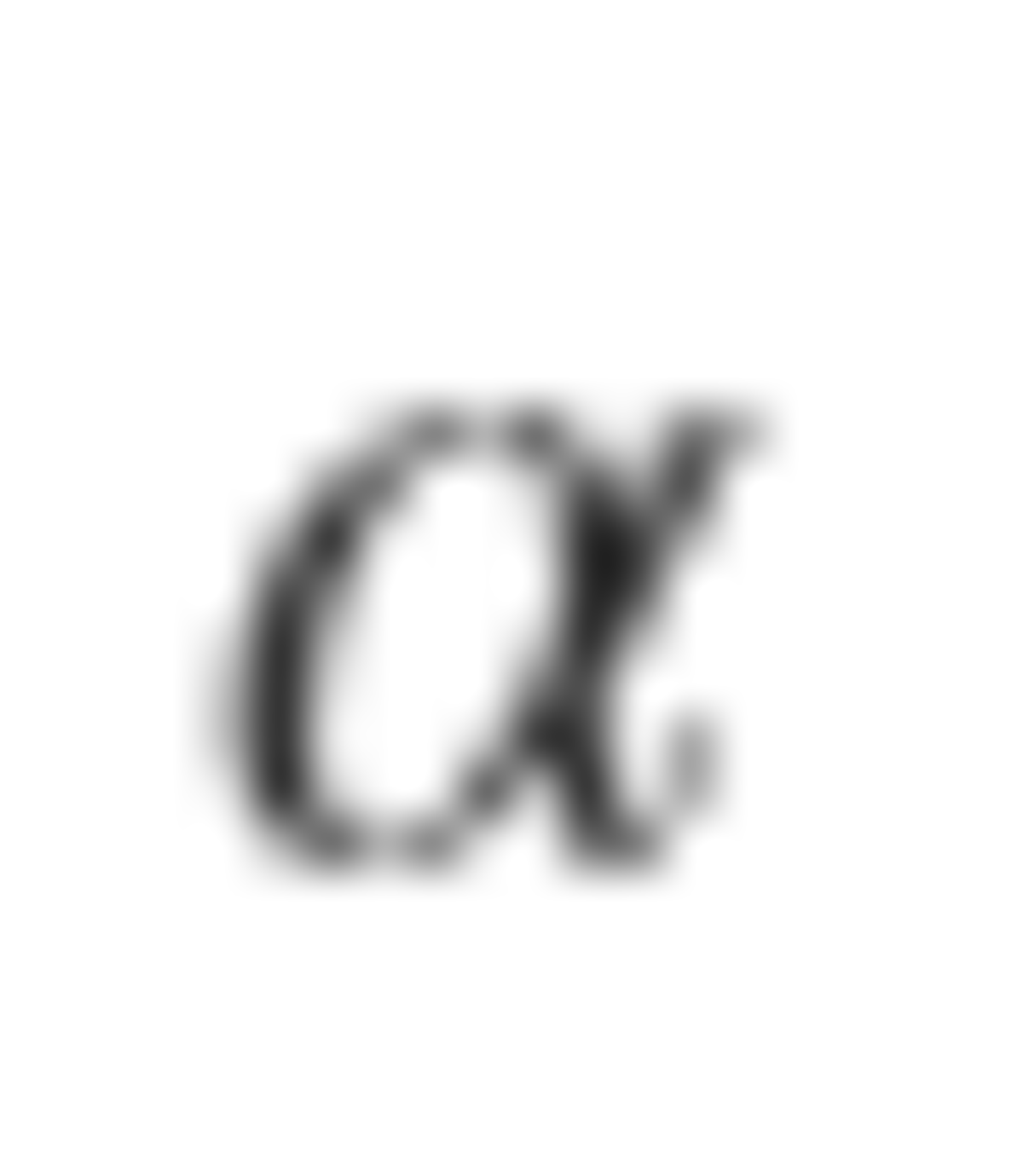
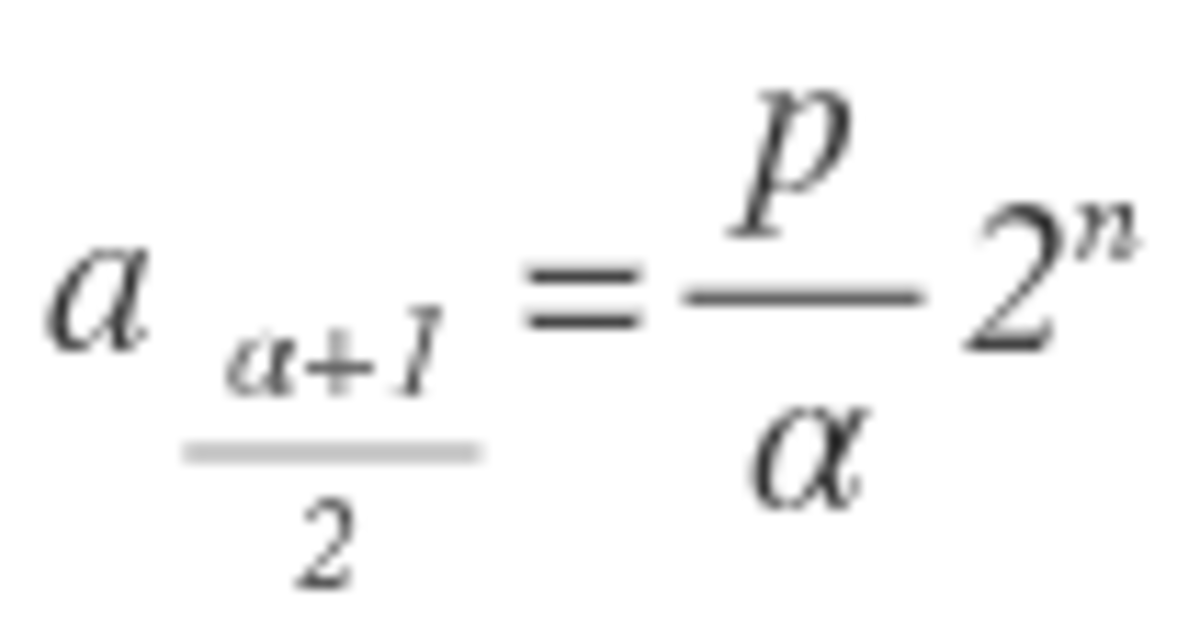
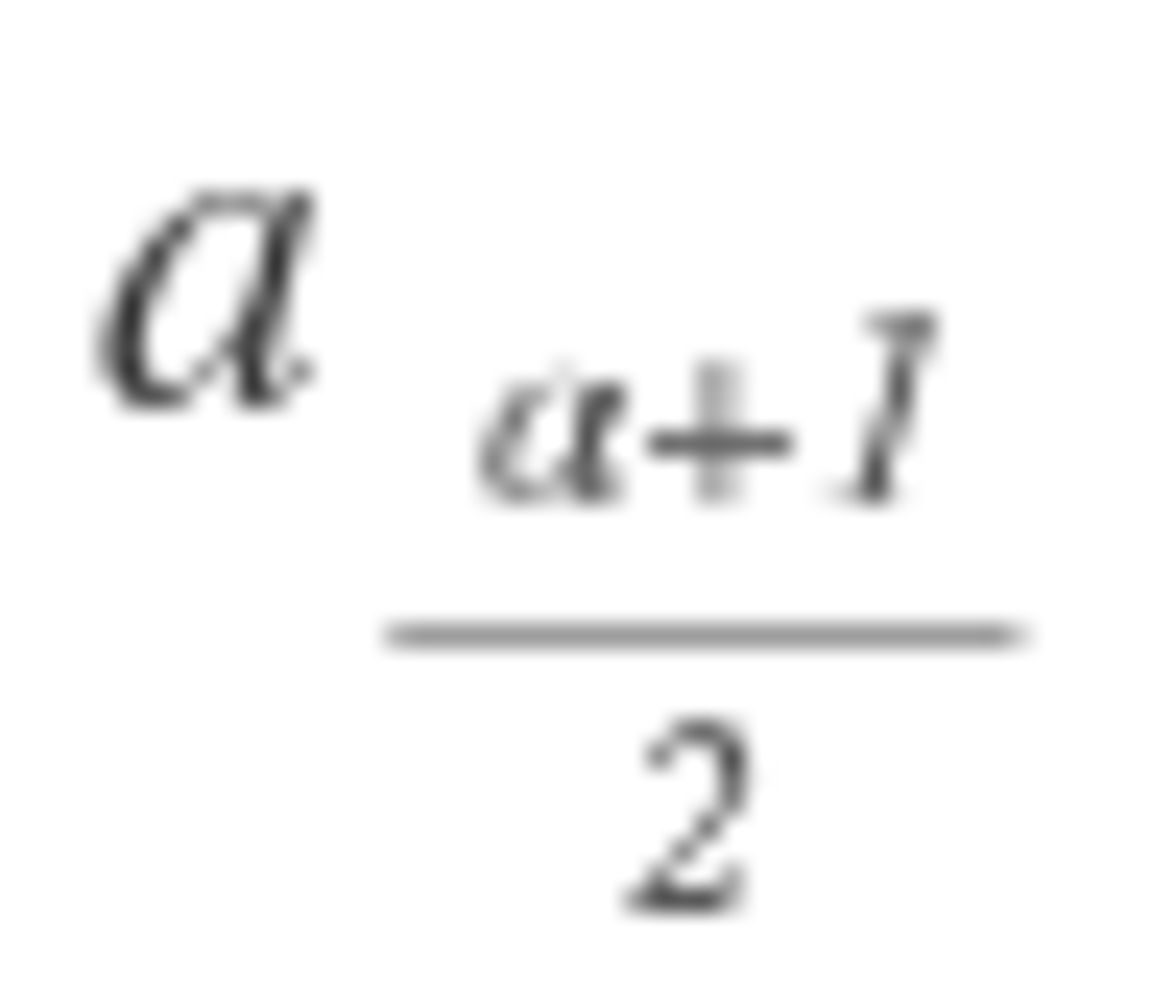
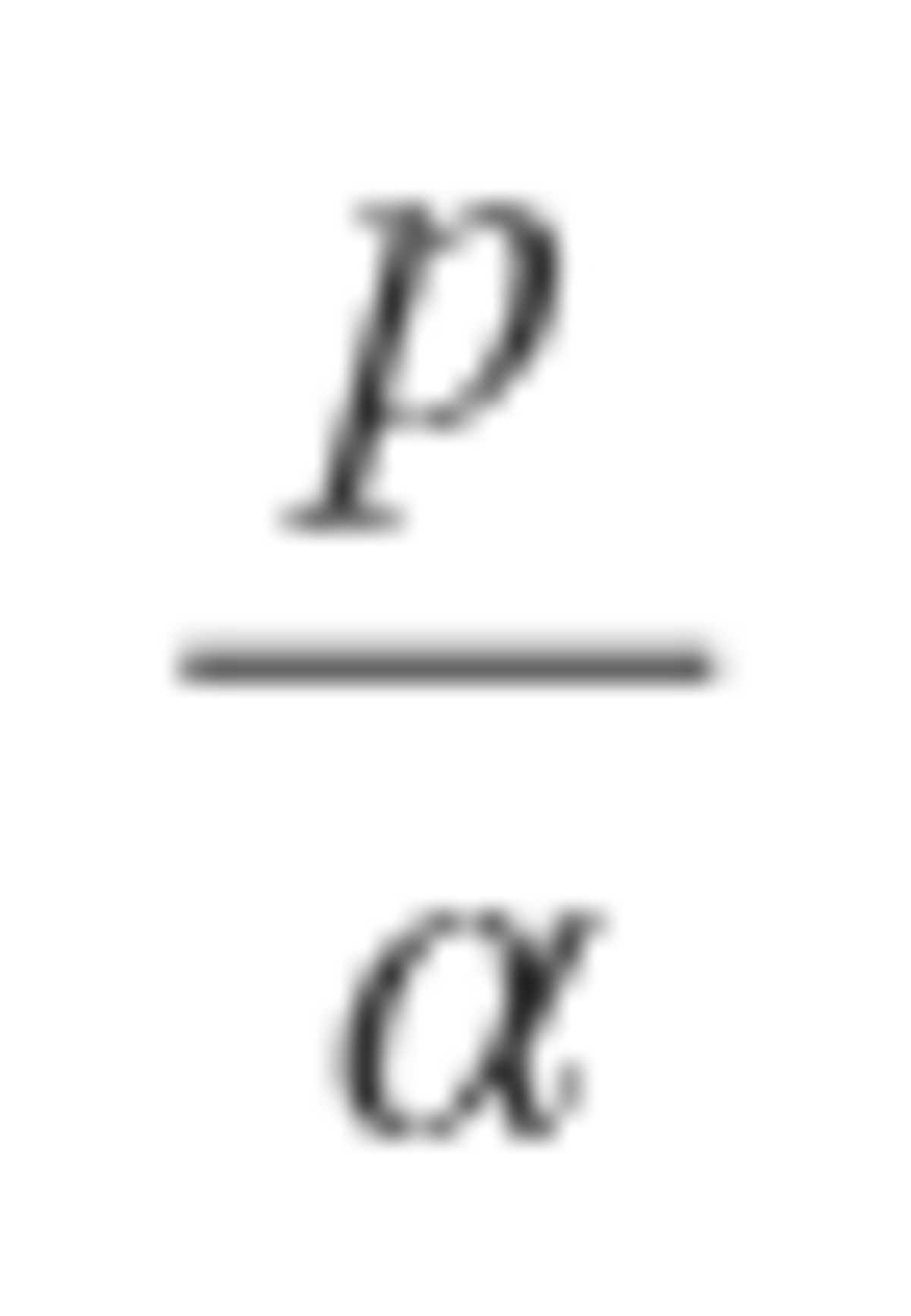
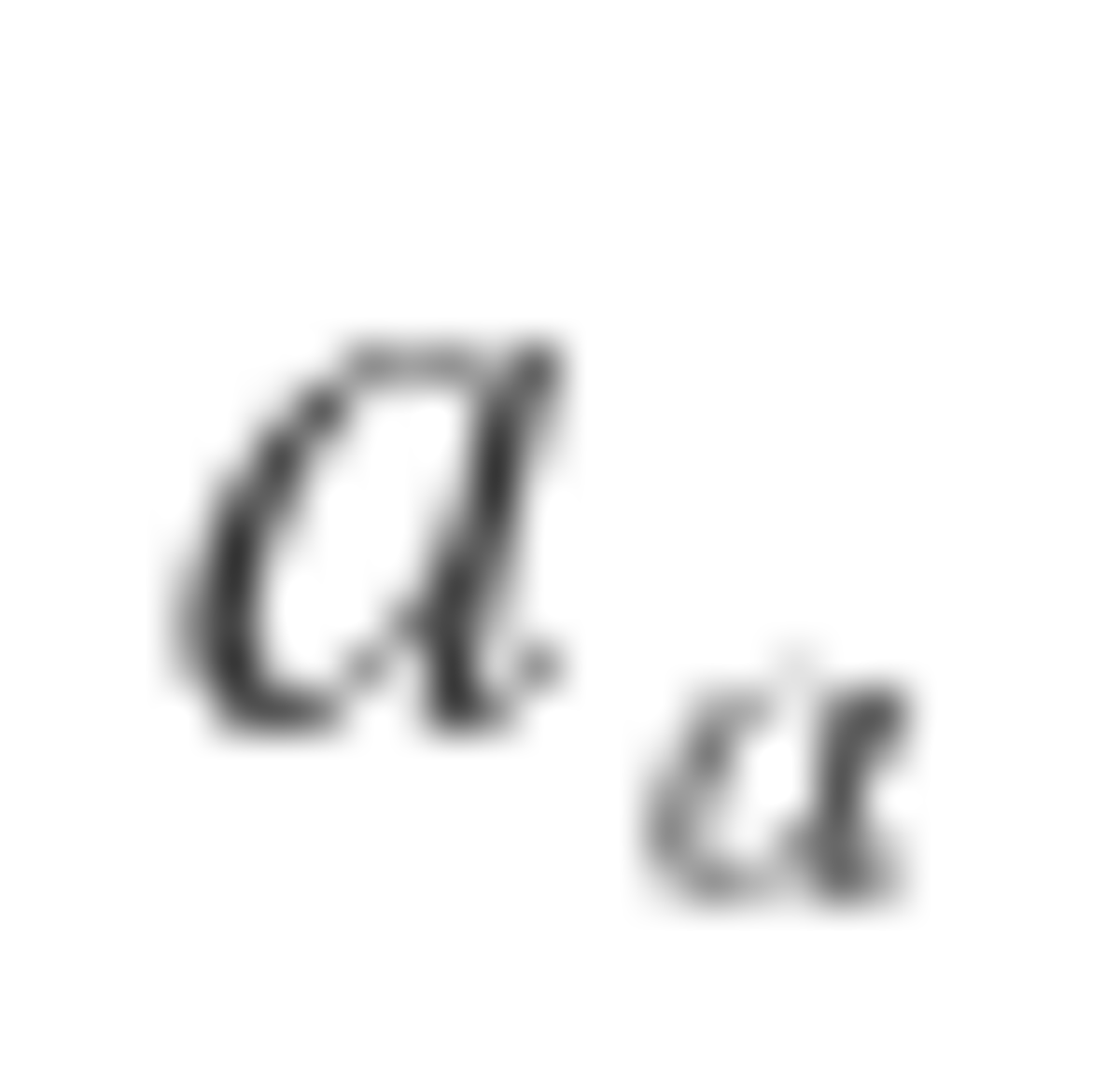
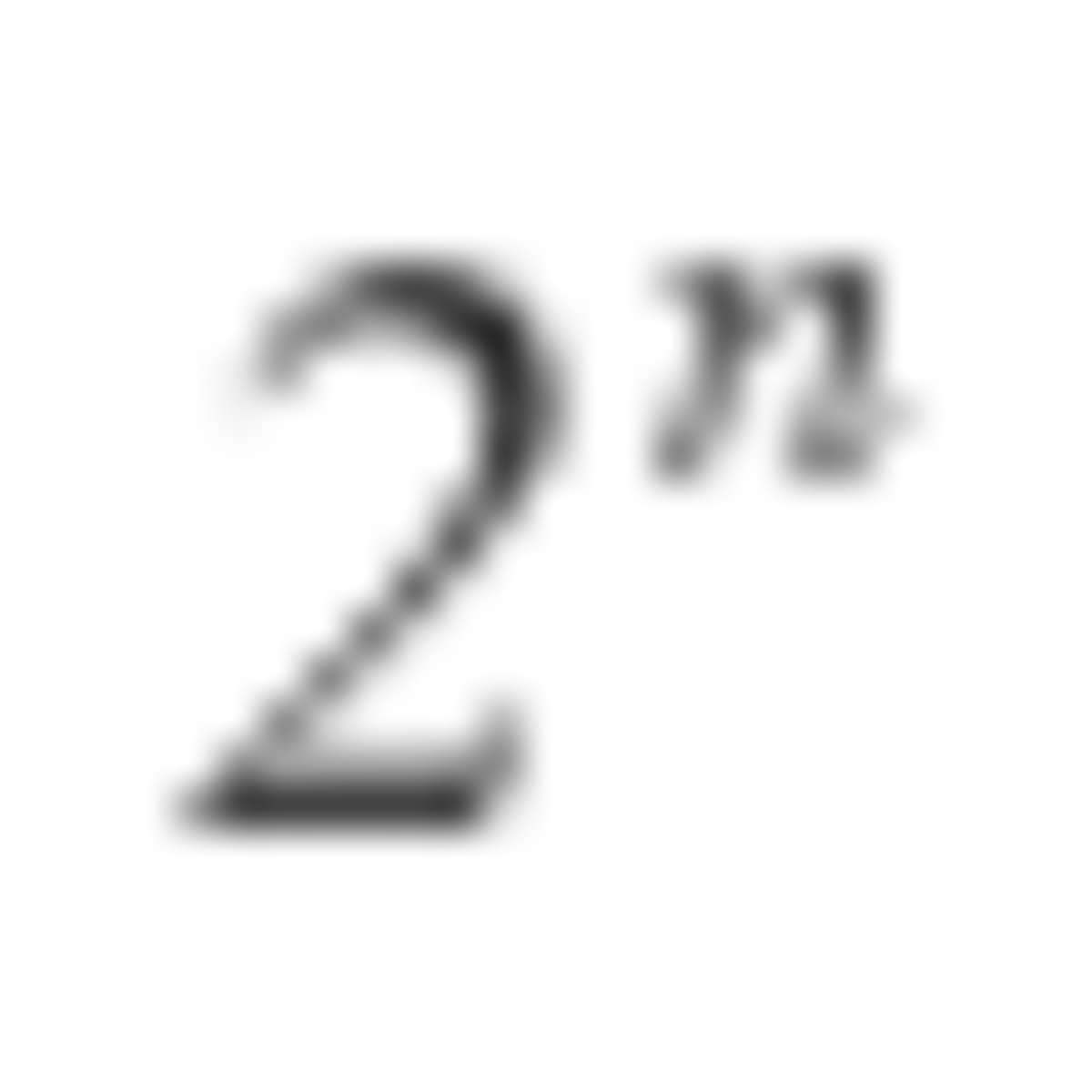
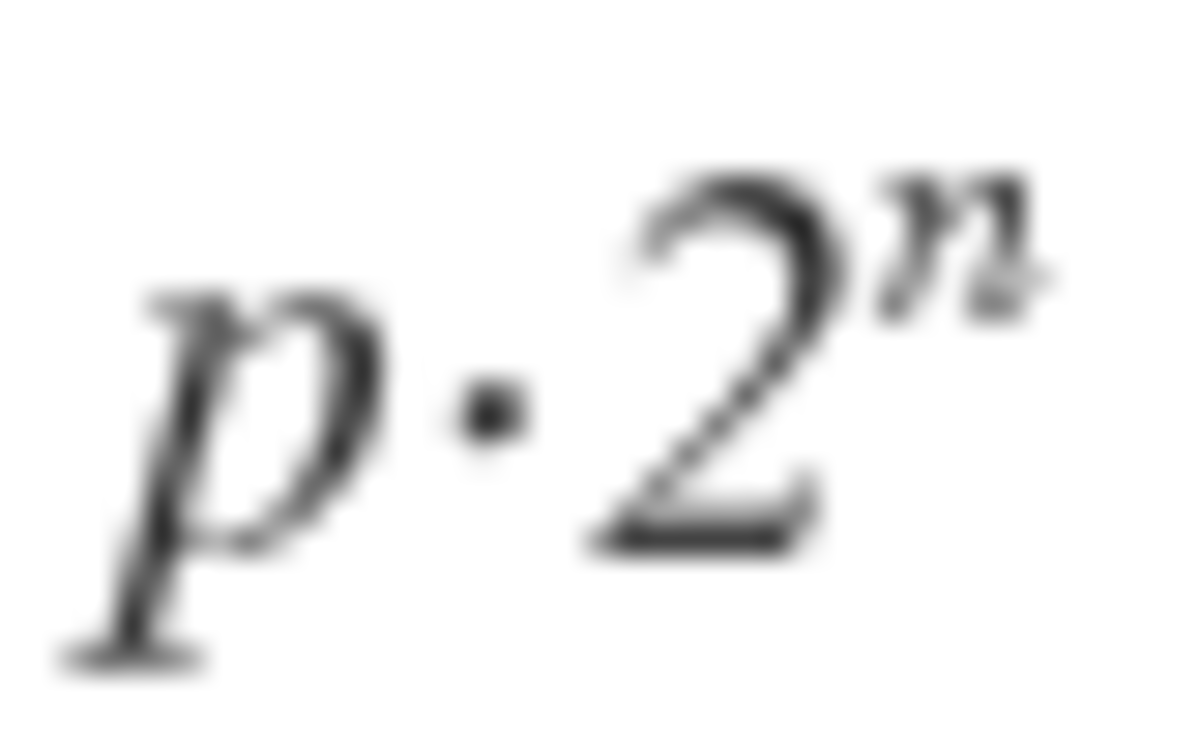
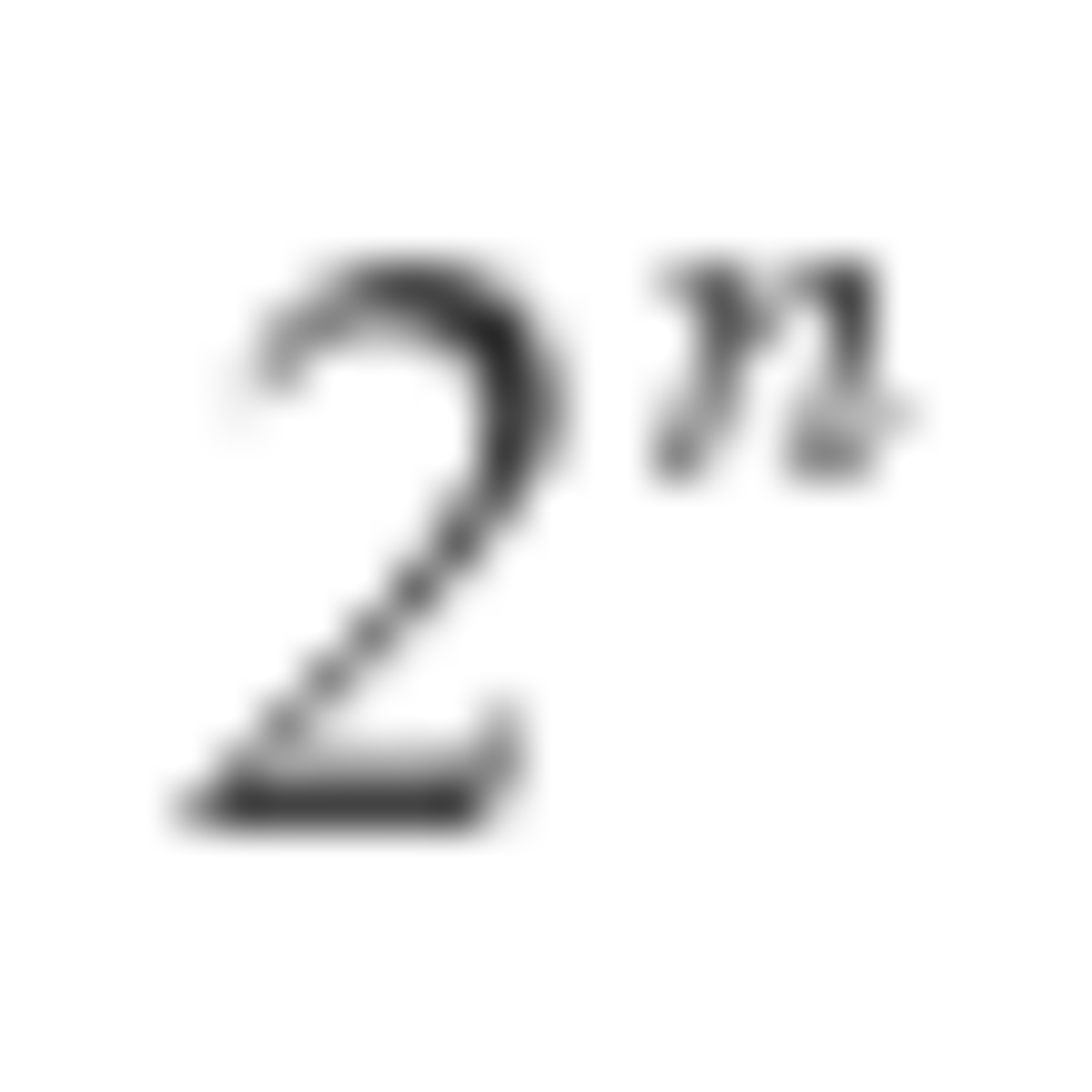
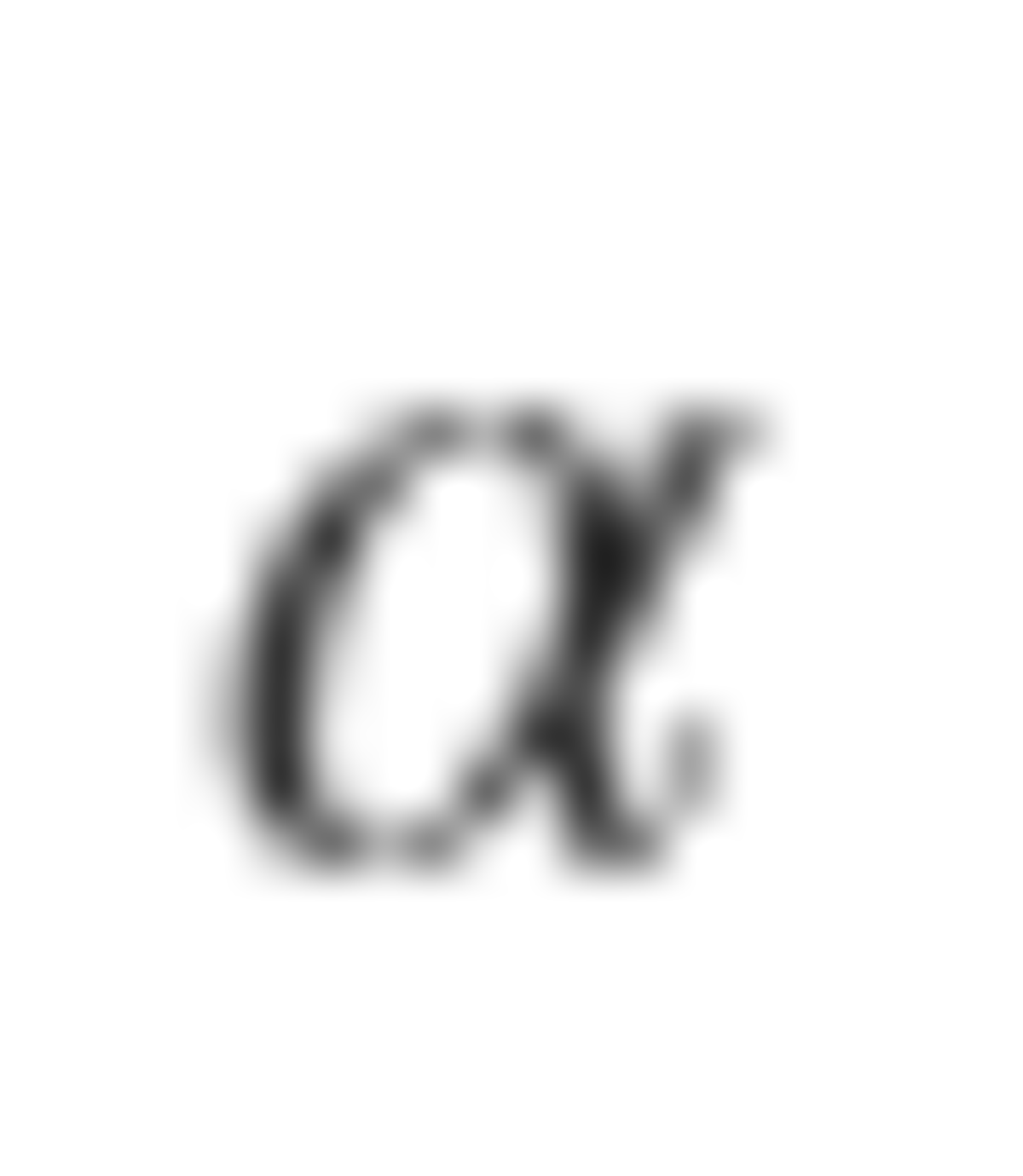
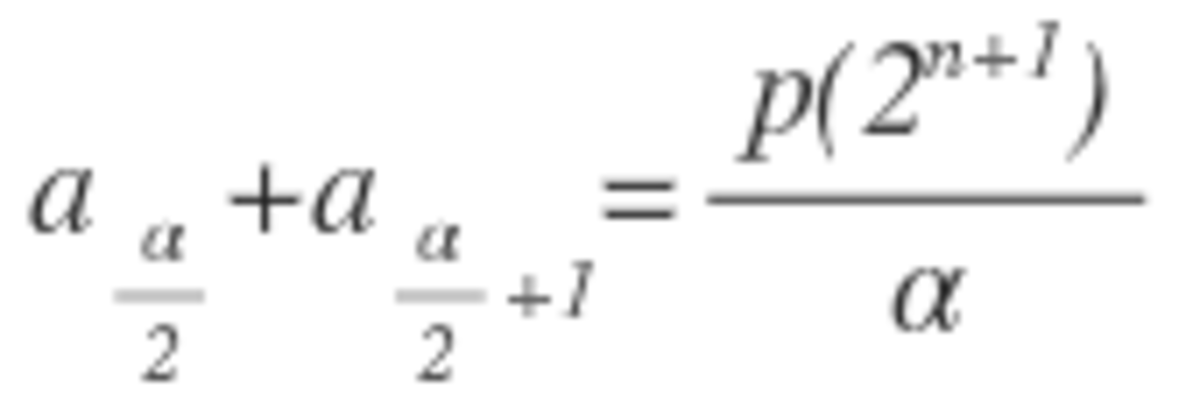
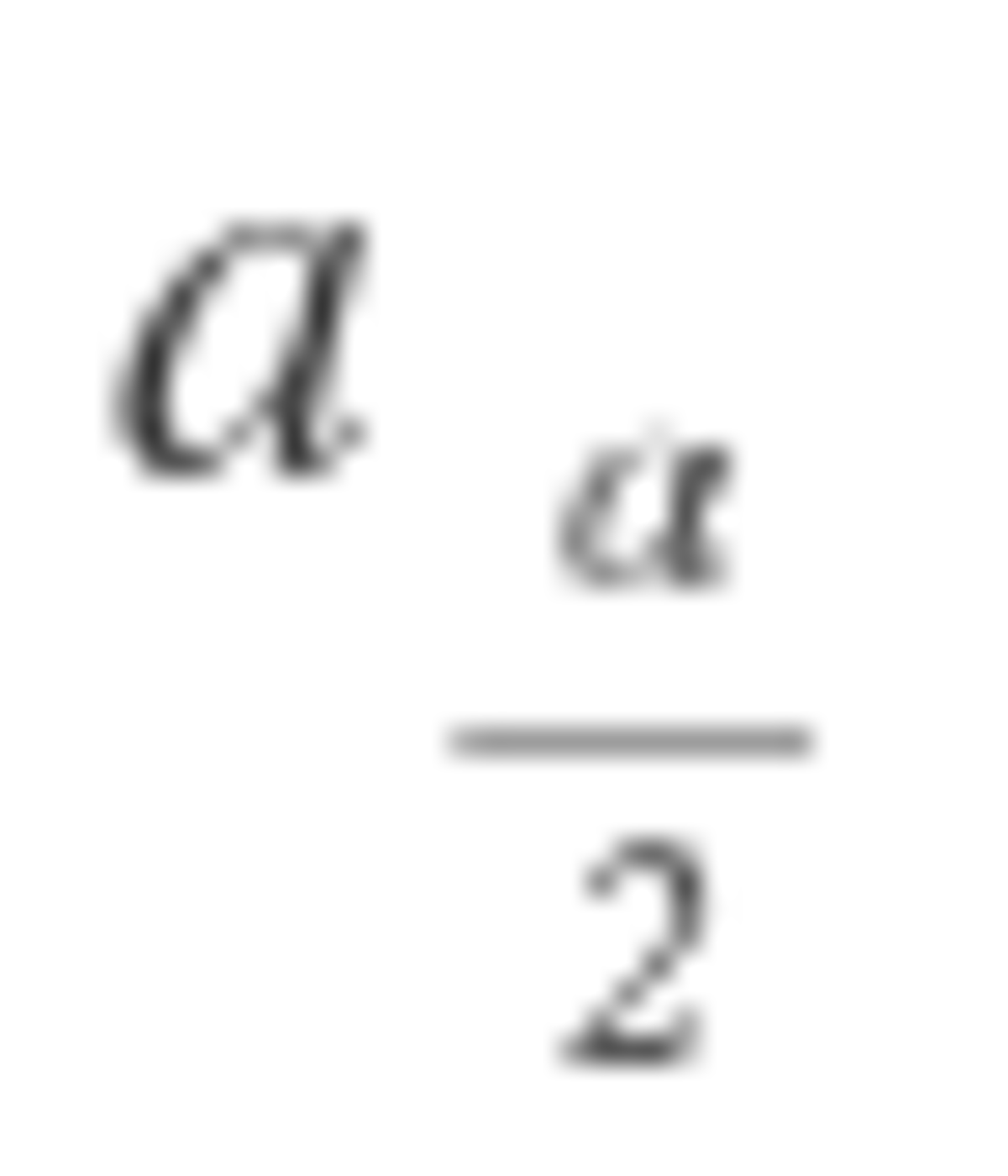
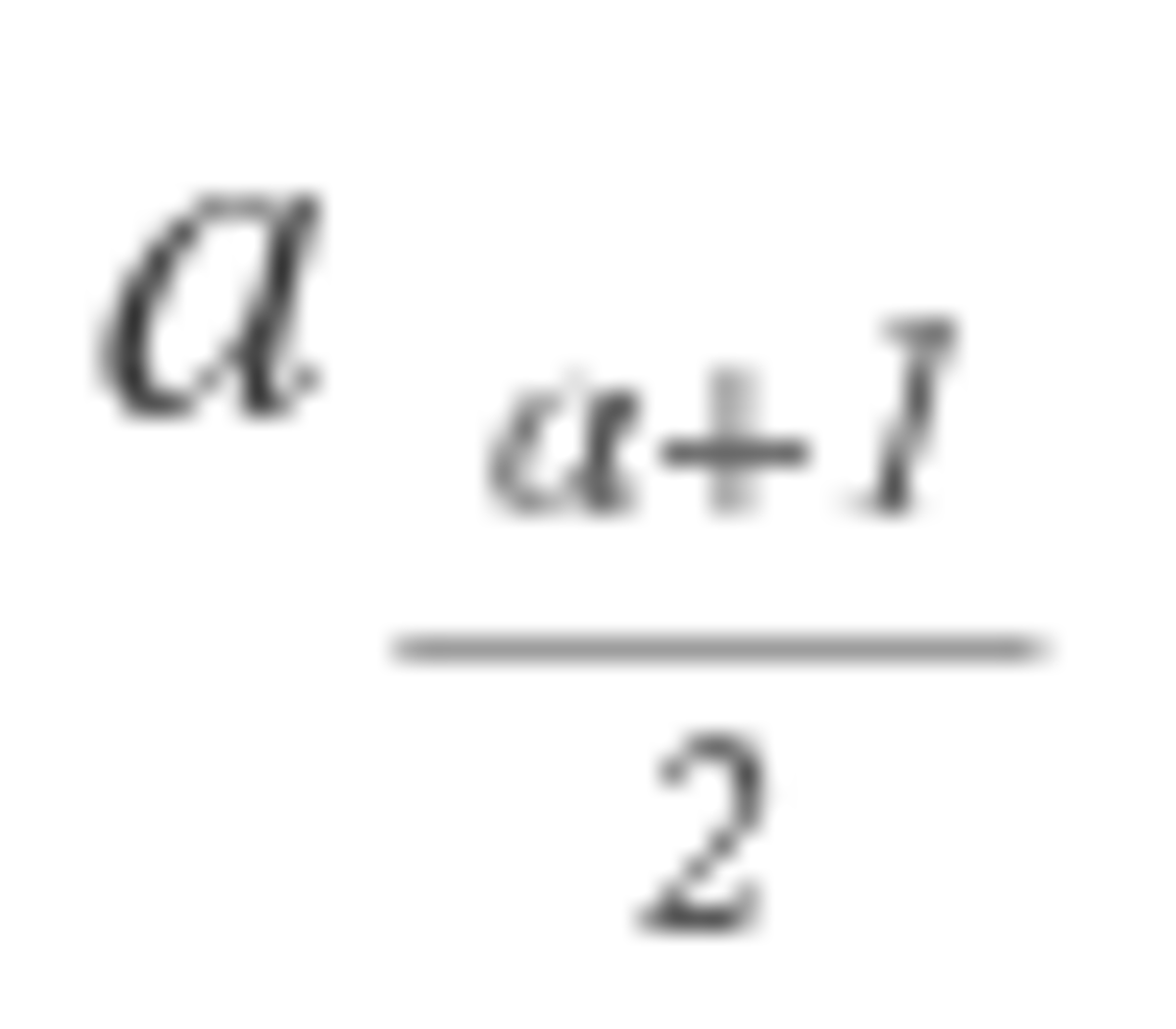
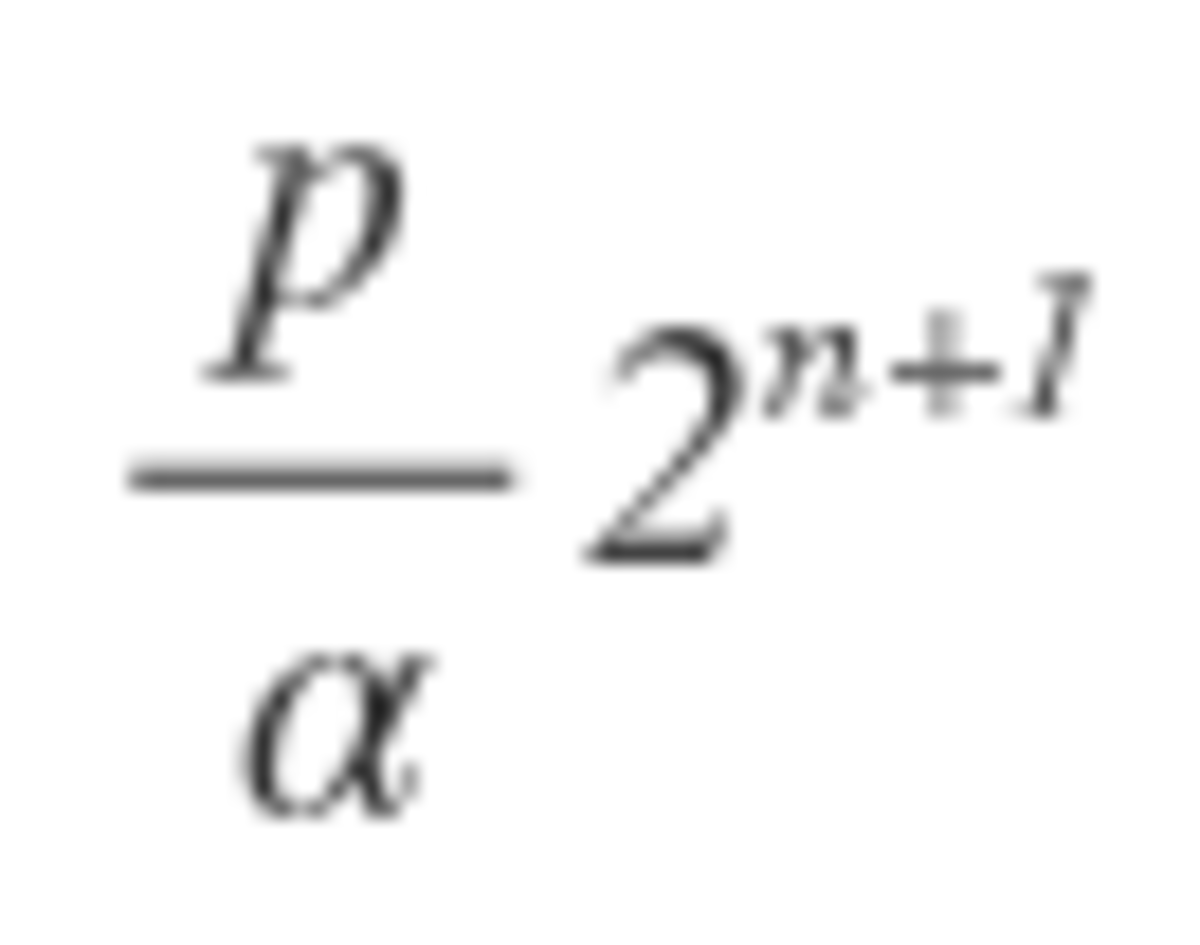
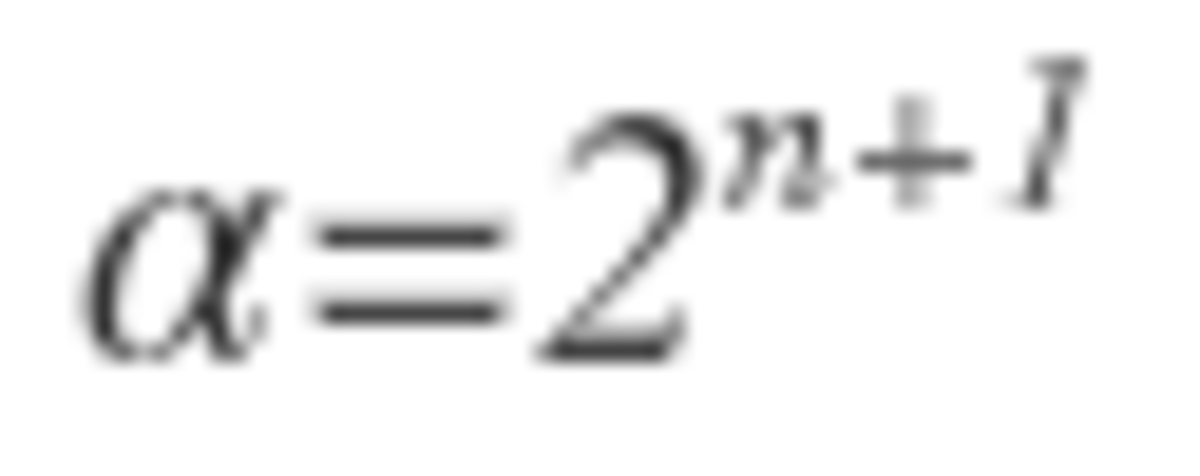
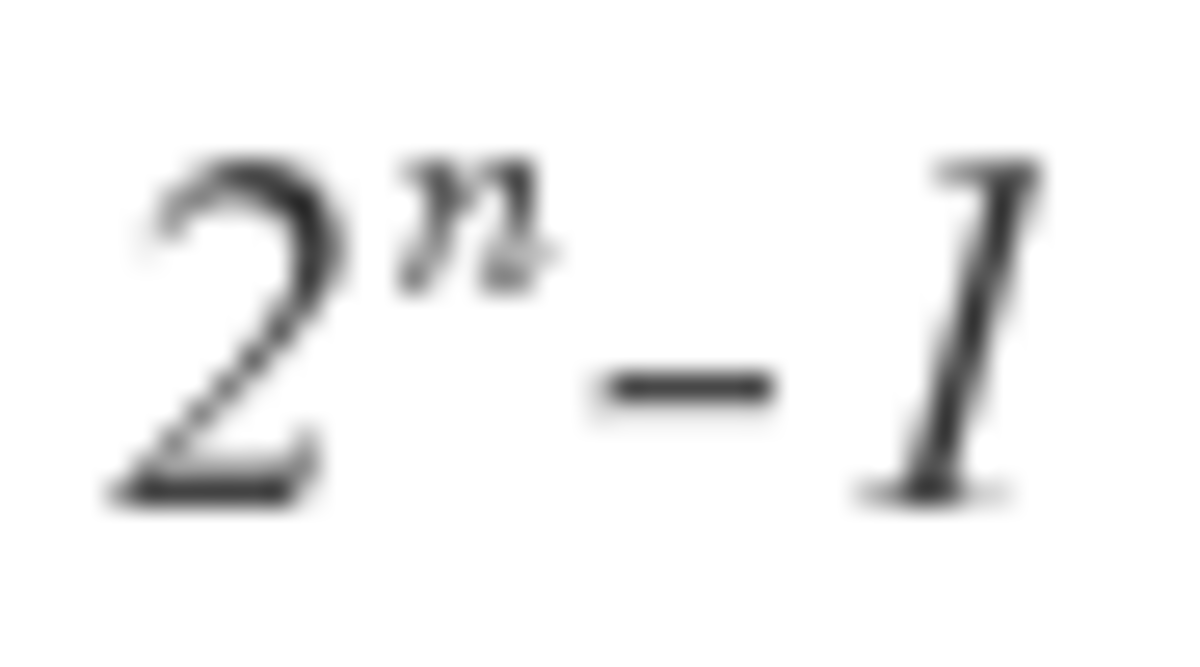
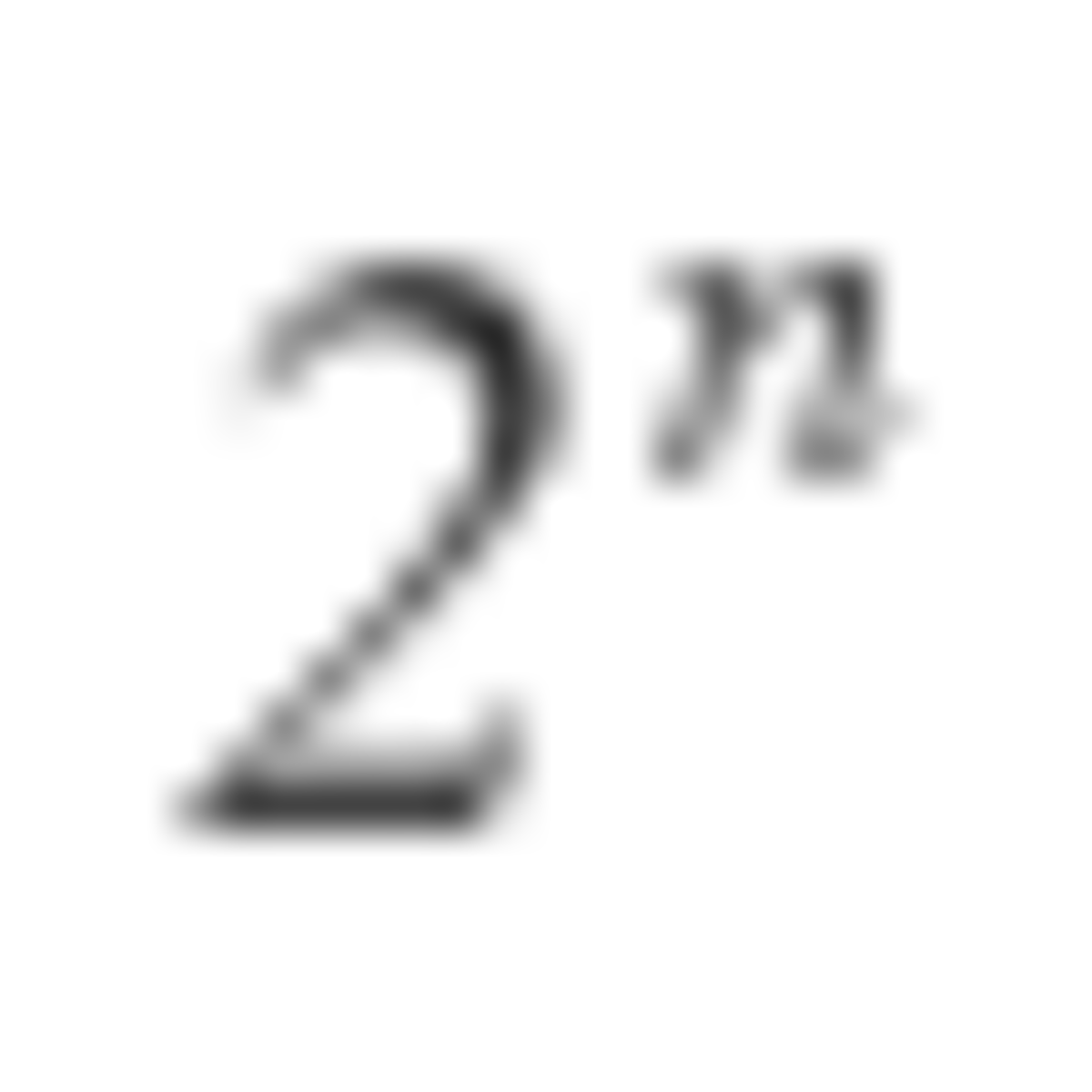
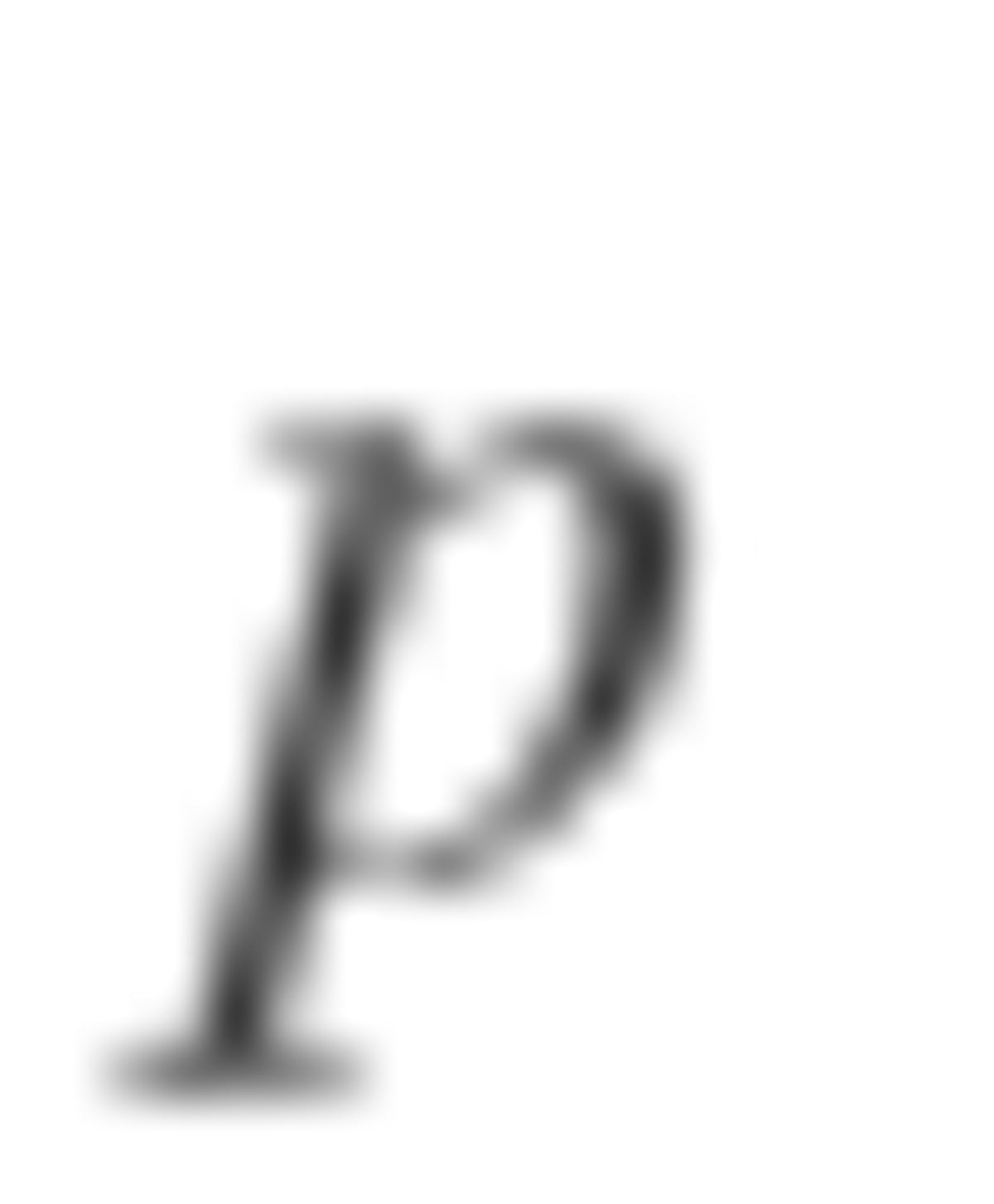
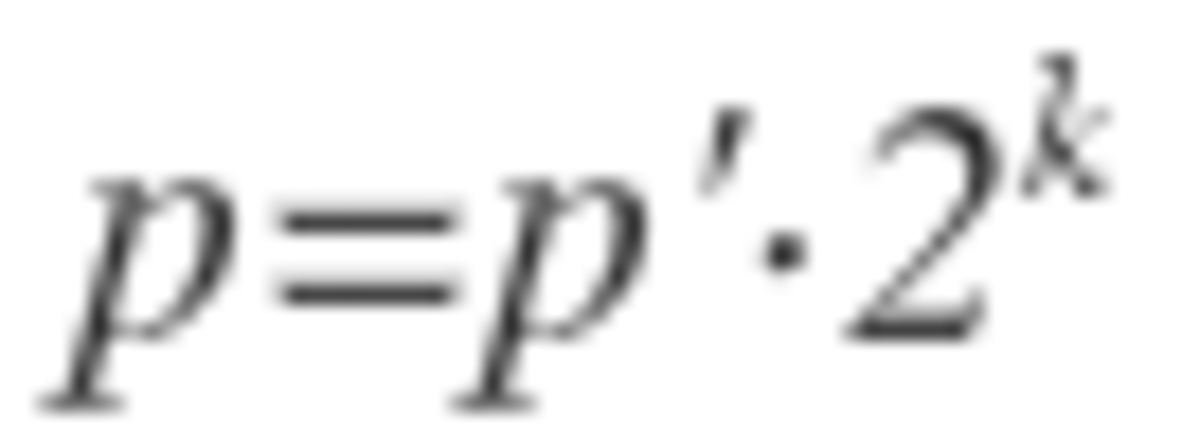
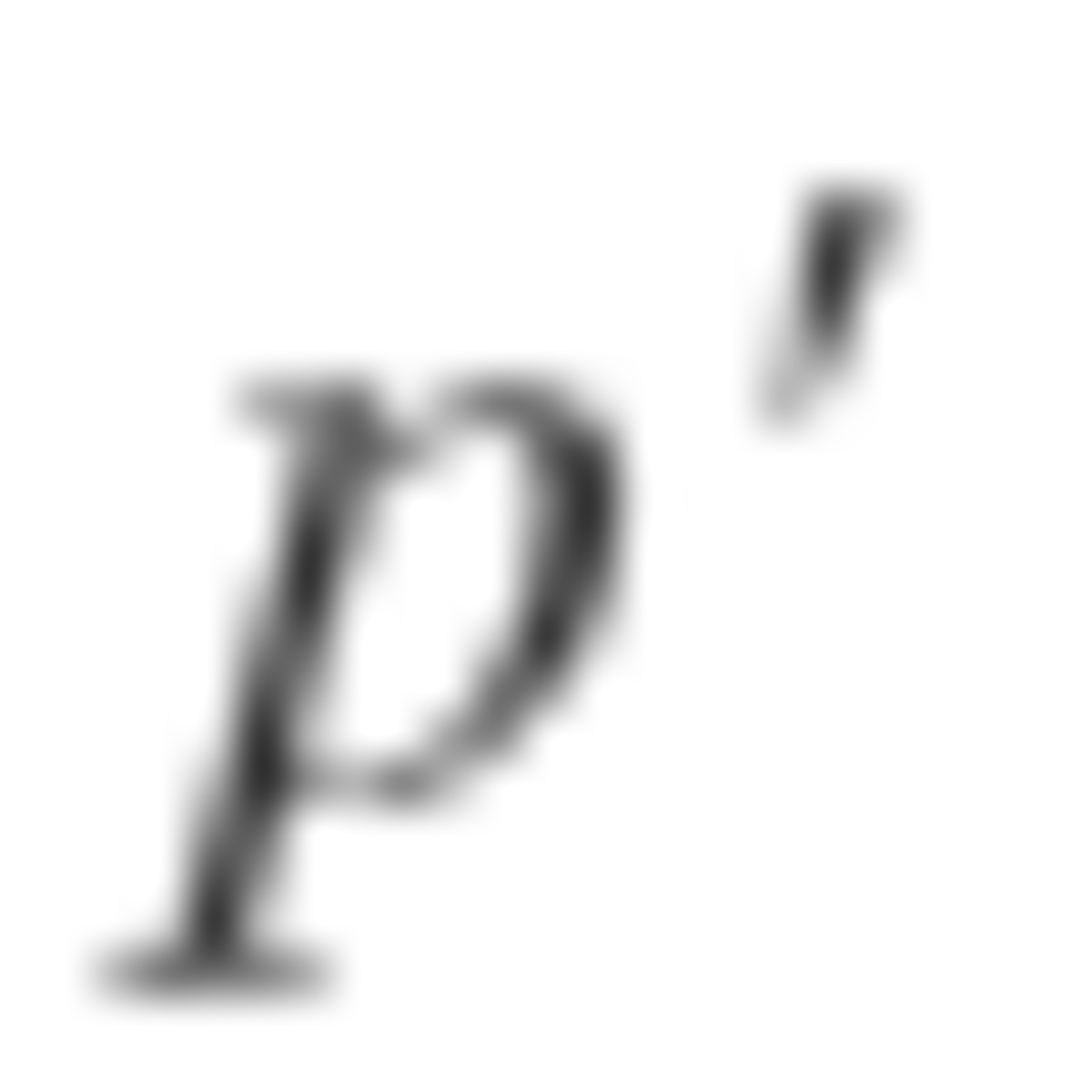
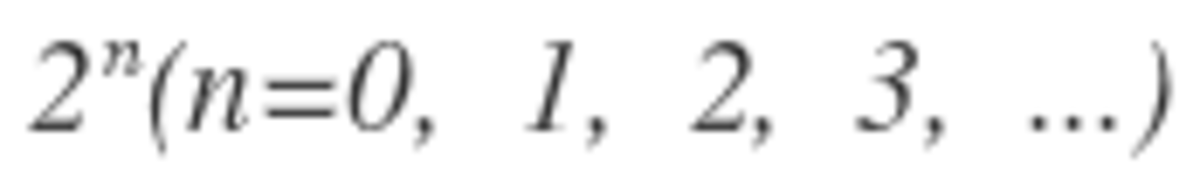
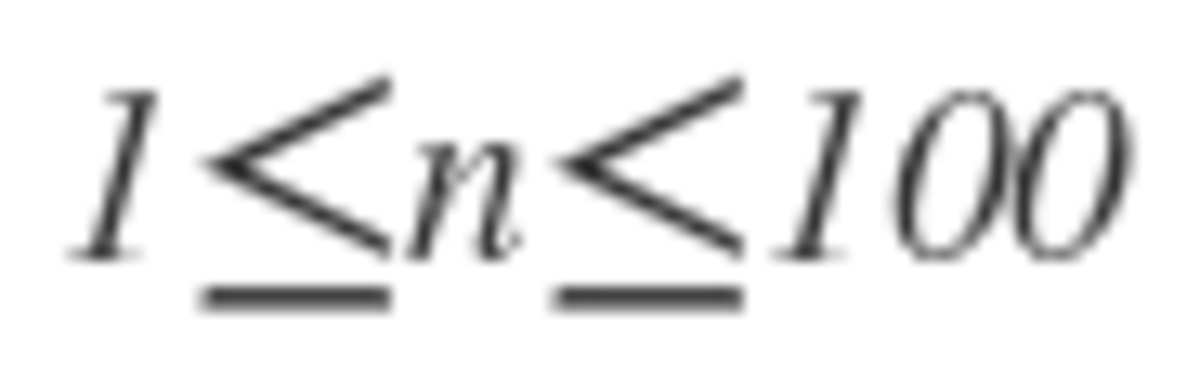
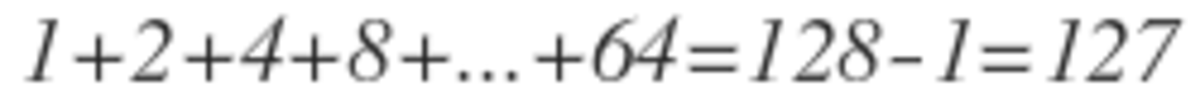
It turns out that the bomb is evenly distributed when n is a power of 2. So, 1 + 2 + 4 + . . . + 6 4 = 1 2 8 − 1 = 1 2 7
Proving this is harder.
Part 1: Powers of two work
Let n = 2 k , k ≥ 1 . Suppose the bomb is held by the same person twice. Then there are two integers 0 ≤ a < b ≤ 2 k − 1 for which the bomb is on the same person at a seconds and b seconds. At s seconds, the bomb is 1 + 2 + 3 + . . . + s = 2 s ( s + 1 ) places counter-clockwise from the ending space.
Thus we have 2 a ( a + 1 ) ≡ 2 b ( b + 1 ) ( m o d 2 k )
2 k + 1 ∣ ( a ( a + 1 ) − b ( b + 1 )
2 k + 1 ∣ ( a − b ) ( a + b + 1 )
Note (a-b) and (a+b+1) have opposite parity.
If (a-b) is even, we must have 2 k + 1 ∣ ( a − b ) ⟹ a = b due to the restricted range. Contradiction!
If (a+b+1) is even, we must have 2 k + 1 ∣ ( a + b + 1 ) .
However 1 ≤ a + b + 1 ≤ ( 2 k − 1 ) + ( 2 k − 1 ) + 1 = 2 k + 1 − 1 so this is also impossible.
Therefore no such a and b exist by contradiction. □
Part 2: Everything else fails
Let n = 2 k m for some odd m greater than one and some non-negative integer k.
Consider s ∈ S = { 0 , m − 1 , 2 m − 1 , 3 m − 1 , . . . , 2 k m − 1 }
We have m ∣ 2 s ( s + 1 ) since m is odd.
Therefore 2 s ( s + 1 ) is congruent to one of R = { 0 , m , 2 m , 3 m , . . . , ( 2 k − 1 ) m } modulo 2 k m .
As ∣ S ∣ = 2 k + 1 > 2 k = ∣ R ∣ we will have some repeat by the pigeonhole principle.
Therefore for some two values in S, the bomb will be the same number of places counterclockwise from the ending space, that is, they will be in the same place. □
Note that when m=1, m − 1 = 0 , so ∣ S ∣ = ∣ R ∣ and there is no problem.