Time required for the cylinder to stop?
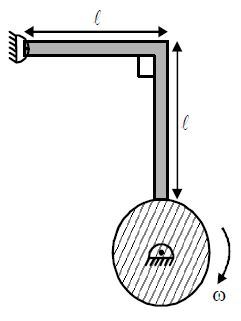 Figure shows a uniform rigid rod of
shape whose mass is
and is lying in a vertical plane. It is hinged at one end and the other end is rubbing with a rotating solid cylinder of mass
and radius
. If the initial angular velocity of the cylinder is
. Co-efficient of friction between the rod and the cylinder is
.
Figure shows a uniform rigid rod of
shape whose mass is
and is lying in a vertical plane. It is hinged at one end and the other end is rubbing with a rotating solid cylinder of mass
and radius
. If the initial angular velocity of the cylinder is
. Co-efficient of friction between the rod and the cylinder is
.
After how much time (in second) will the cylinder stop rotating?
Take .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.