Time Series Asset Probability
Let’s say the price of an asset behaves as follows:
The asset price starts from 0 At any time t, the price is equally likely to go up or down by 1 i.e. Price(t+1) can only be Price(t) + 1 or Price(t) – 1, and both of those are equally likely However, if the price goes to 10, it has to go back to 9 at the next instant. If the price goes to -10, it has to go back to -9 at the next instant. That is, if Price(t) = 10, Price(t+1) has to be 9. If Price(t) = -10, Price(t+1) has to be -9.
What is the Fair Value of the Asset(Expected Value)?
Calculate Probability of Asset being each of the Values(i.e -10 to +10)?
Prove that ExpectedValue(t)=ExpectedValue(t+1)?
Answer contains this Question
If current price of the stock is 0, what is the probability that stock price goes to 2 before it goes to -4?
Note:Please try to explain by equations and not by intuition because of the symmetries involved.
Please see the attachment for a visual representation
Also if you can refer resources to learn these type of problems, it would be great!
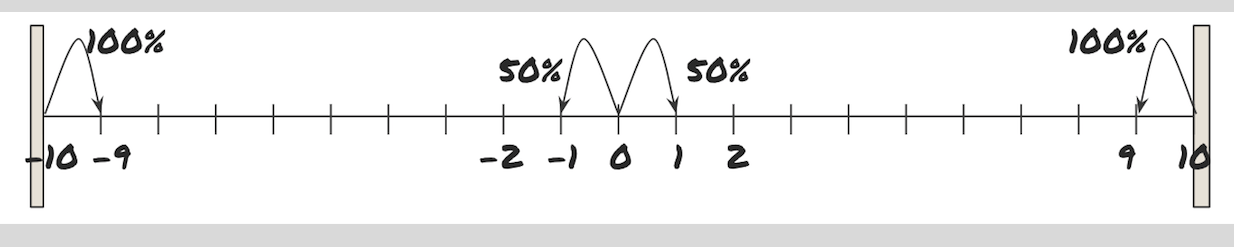
The answer is 0.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!