Time taken for travelling along a parabolic arc
An object moves along the path in meters. It moves with a velocity given by . It starts its motion at the point , after what time will the object reach the point . Express your answer in seconds.
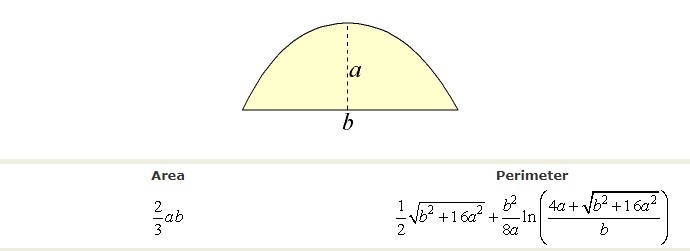
Reference: Parabola - Area and Perimeter
The answer is 6.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The length of curve is given by
s = ∫ a b 1 + ( d x d y ) 2 d x = ∫ − 3 3 1 + ( 2 x ) 2 d x = 2 ∫ 0 3 1 + ( 2 x ) 2 d x = ∫ 0 tan − 1 6 sec 3 θ d θ = tan θ sec θ ∣ ∣ ∣ ∣ 0 tan − 1 6 − ∫ 0 tan − 1 6 tan 2 θ sec θ d θ = 6 3 7 − ∫ 0 tan − 1 6 sec 3 θ d θ + ∫ 0 tan − 1 6 sec θ d θ = 2 1 ( 6 3 7 + ∫ 0 tan − 1 6 sec θ + tan θ sec 2 θ + tan θ sec θ d θ ) = 2 1 ( 6 3 7 + ln ( sec θ + tan θ ) ∣ ∣ ∣ ∣ 0 tan − 1 6 ) = 2 1 ( 6 3 7 + ln ( 3 7 + 6 ) ) ≈ 1 9 . 4 9 4 1 7 7 5 2 For y = x 2 from ( − 3 , 9 ) → ( 3 , 9 ) Since the integral is even Let tan θ = 2 x ⟹ sec 2 θ d θ = 2 d x By integration by parts Note that s = ∫ 0 tan − 1 6 sec 3 θ d θ Multiply up and down by sec θ + tan θ
Therefore the time to travel from P to Q is t ≈ 3 1 9 . 4 9 4 1 7 7 5 2 ≈ 6 . 4 9 8 .