Rectangle Array
The big rectangle above is composed of 5 small identical rectangles. If the perimeter of the big rectangle is 80, then what is the area of a small rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
In general, for a clearer solution, we'd like to introduce as few variables as possible. Since the width and height of the small rectangles are dependent on each other in a clear way, the strategy of using only a single variable works well here.
Clear and concise solution
I understand everything but at the perimeter of the big rectangle it where is the 2 came from
Log in to reply
Math formula:
Perimeter of rectangle=sum of the length of four sides =length+breadth+length+breadth =2(length+breadth)
I hope now it will be clear for you.
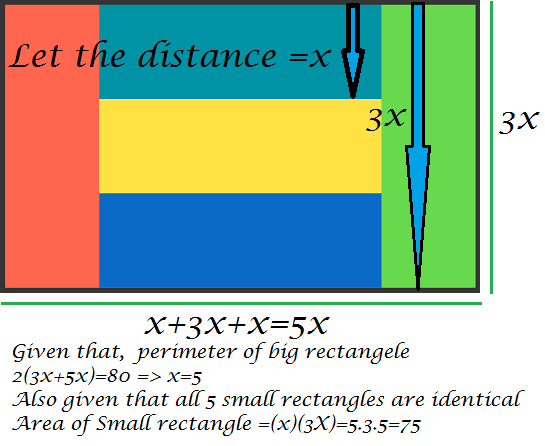
Let's label the sides of the small rectangle x and y , as shown above.
We are given that the P b i g = 8 0 . Thus,
4 x + 4 y = 8 0 ⟹ x + y = 2 0
We also know that because the big rectangle is made of up 5 small identical rectangles, A b i g = 5 × A s m a l l . Thus,
( 2 y + x ) ( x ) = 5 x y
2 x y + x 2 = 5 x y
x 2 = 3 x y
x = 3 y
x + y = 2 0 ⟹ 3 y + y = 2 0 ⟹ y = 5
x = 2 0 − 5 = 1 5
Finally,
A s m a l l = x y = 1 5 × 5 = 7 5
Oh, I like how you equated the area. That might give me more space to play with in future problems.
In your solution, the goal of equating the area is to get the condition x = 3 y . Do you see how to tell that immediately from the diagram?
Why not directly deduce that x = 3 y because it is clear from the fact that 3 breadths of the small rectangle make its length; visible in the centre of the diagram.
Wow...I used this exact same method. What are the chances? This problem wouldn't be equally solvable if the middle three rectangles converged.
Note that the rectangle's dimensions are x by 3x
Therefore, the entire rectangle has a height of 3x and a width of (1 + 3 + 1)x = 5x
Therefore, the perimeter = (3+3+5+5)x=16x=80 --- > x=5
Therefore, the large rectangle has dimensions (3 * 5) by (5 * 5).
The area of a small rectangle is 1/5th the area of the large rectangle - so (3 * 5)(5 * 5)/5 = 3 * 25 = 75 is the answer.
How do we know that the rectangle's dimensions are x by 3x here?
The large rectangle is made of five equally-sized rectangles, so we can divide each rectangle into three squares. After which, we get that there are five equally-sized squares on the long side and three equally sized squares on the short size; 5+5+3+3 = 16 is the new perimeter. Since both sides of a square are equal, we can divide 80 by 16 to get 5. Going back to that a rectangle is made of three equally sized squares, we can find the area of one square and multiply it by three to get the area of one of the rectangles.
Nice observation by splitting the small rectangles into squares.
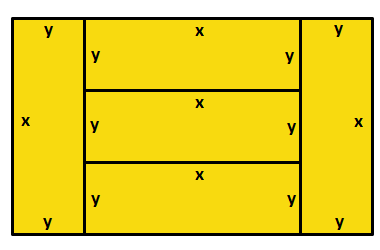
Let l and w be the length and width of the small rectangle, respectively. Then, the length and width of the big rectangle is l + 2 w and l respectively.
Given that the perimeter of the big rectangle is 8 0 , we must have that 2 ( l + ( l + 2 w ) ) = 8 0 ; this reduces to l + w = 2 0 . Given the area of the small rectangle is l w , the area of the large rectangle can be evaluated to 5 l w . But it is also equal to l ( l + 2 w ; equating the two gives the expression l = 3 w .
Therefore, the perimeter equation satisfies 4 w = 2 0 , which implies w = 5 and l = 1 5 . Hence, the area of the small rectangle is 7 5 , as required.
Nice solution. The essential point here was to notice that l = 3 w
Very Nice explanation.