Tiny angle
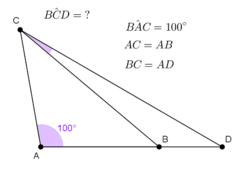 In triangle
C
A
D
we have
C
A
D
^
=
1
0
0
°
. Point
B
in on
A
D
such that
A
C
=
A
B
and
B
C
=
A
D
. Find
B
C
D
^
in degrees.
In triangle
C
A
D
we have
C
A
D
^
=
1
0
0
°
. Point
B
in on
A
D
such that
A
C
=
A
B
and
B
C
=
A
D
. Find
B
C
D
^
in degrees.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
how
Log in to reply
Which part you didn't understand? If it's where to draw the equilateral then I suggest you to draw it , as if CA is a segment of that equilateral. Meaning take the point E on the left side of CA.
awesome!
Brilliant ! bravo !
awesome answer
Draw the sketch,pls
really great
can you please explain it in a simpler way?
Can you please draw the diagram wherein you have mentioned about traingle CAE please.
Soul you pls show the sketch?
Write a comment or ask a question... Awesome. I liked this problem. Strange, I also solved this problem is this way.
good
It was like a piece of cake for me.
while E is a point that links A and C to form an equilateral, how can EAB be an isosceles?
I used only 2 equations to solve this problem. First, i assumed that AC = a, and AD = b.
It says that angle A = 100, since triangle CAB is isosceles, the other two angles must be 40 each. Then angle C = 40 + theta. So for the whole triangle i have angle A and angle C but how about D?
What i did for angle D is i subtracted angle A and C to 180, so D = 40 - theta. Then use sine law but we have to use angle C and angle D, not A... Thats the first equation. If you perform this, youll see that there are 3 unknown variables; a, b, and theta.
So for second equation, you will use sine law again but we are focusing on tringle CAB. Then you would get b/sin100 = a/sin40. Which is also equal to b = a (sin100/sin40). Then substitute it to the first equation then youll see that a would gone and you only have theta as a variable. For sin(40 + theta) and sin (40 - theta), youll use the another sine law.
Sin ( a+b ) = sin a cos b + cos a sin b, it is respect to its operation, only at this technique. Then just perform the problem then youll get 9. 999999.... Which is almost equal to 10... Thats all
why EC+CA??? its not same. cz point A is weight point of triagle EBC.
wooah all wonderful i am the student of 9 class plz make questions for me
Wonderful solution!
Wow, I've to say that you did a wonderful solution! Conhgratulations
??????????
Sketch please?
Log in to reply
what
yes. please
Assume AC = 1 unit, therefore AB = 1 unit, angle ACB = angle ABC = 40
Using sine law, we will get BC = 1.53 units
Therefore AD = 1.53 units and BD = AD-AB = 1.53-1 = 0.53 unit
Angle CBD = 140
Using cosine law, we will get CD = 1.97 units
Now, using sine law, we will get angle BCD = 10 degrees
We can get sine of obtuse angle also as +ve
Hey nice solution I understood this one
solution interesting.....
First apply sine rule in ACB triangle we get eq as BC/sin(100)=AC/sin(40)=AB/sin(40) Then apply sine rule in triangleACD AD/sin(40+x)=AC/sin(40-x) Replace AD by BC Then from the two eqations we get Sin(100)/sin(40)=sin(40+x)/sin(40-x)
By solving above equation by using componendo dividendo rule we get dol as x=10
My solution applying sine rule was:
△ A B C : B C A C = s i n ( 1 0 0 ° ) s i n ( 4 0 ° )
△ A C D : A D A C = s i n ( 4 0 ° + x ) s i n ( 4 0 ° − x )
since B C = A D , we get:
s i n ( 4 0 ° + x ) s i n ( 4 0 ° − x ) = s i n ( 1 0 0 ° ) s i n ( 4 0 ° )
we know s i n ( 1 0 0 ° ) = s i n ( 8 0 ° ) = 2 s i n ( 4 0 ° ) c o s ( 4 0 ° ) . Then, we can rewrite the above equation as:
s i n ( 4 0 ° + x ) s i n ( 4 0 ° − x ) = 2 s i n ( 4 0 ° ) c o s ( 4 0 ° ) s i n ( 4 0 ° ) = 2 c o s ( 4 0 ° ) 1
and, then:
2 1 s i n ( 4 0 ° + x ) = c o s ( 4 0 ° ) s i n ( 4 0 ° − x )
remembering that s i n ( 3 0 ° ) = 2 1 and s i n ( 5 0 ° ) = c o s ( 4 0 ° ) , we have:
s i n ( 3 0 ° ) s i n ( 4 0 ° + x ) = s i n ( 5 0 ° ) s i n ( 4 0 ° − x )
Now we need to remember the Product-to-sum/sum-to-product Identities :
c o s ( α + β ) − c o s ( α − β ) = − 2 ⋅ s i n ( α ) ⋅ s i n ( β )
Applying it to our equation, we get:
c o s ( 7 0 ° + x ) − c o s ( 1 0 ° + x ) = c o s ( 9 0 ° − x ) − c o s ( 1 0 ° + x )
Therefore, c o s ( 7 0 ° + x ) = c o s ( 9 0 ° − x )
and for acute angles:
7 0 ° + x = 9 0 ° − x
∴ x = 1 0 °
Kvsnlr Kvsnlr , Can you please tell me know how to solve using componendo dividendo rule?
the two solutions by Eloy are correct, rest r wrong. those who got answer 20 perhaps imagined CB=BD!
I Found it by using Sine Formulae (Doing Huge Amount Of Calculations) And After This Solution By @Eloy Machado I Feel Wooooowwwww.........Thats Surely Awesome
I solve this differentl. First, i assume a value to known sides.e.g. AC=5,then AB= 5. And then use law of sines. I get BC≈7.6604= AD. And then use law of cosines. I got CD≈9.8480. And then use law of sines. I got 10 for the angle
angle c in BCD = 10 degrees
The easiest way: Extend AD, draw a perpendicular on it. Assume the length of the perpendicular as 10 or whatever u wish. Suppose, AD and perpendicular meets on the point O. Notice angle OCA = 10 degrees and ACB = 40 degrees. Now just use the rule of Tan theta to find the length of OA and Cos \theta to find BC. Since BC = AD, you get the length of OD. Which is 17.31 in my calculation. Now OCD=Tan inverse (17.31/10)=10 degrees (apprx).
triangle ABC is euilateral , so <ACB=<ABC=40 degree. take AC=b,AB=c,BC=a;
applying sine rule ..............
In triangle ABC
a/sin(100) =c/sin(40) =b/sin(40)...................(1)
In triangle ADC
BC=AD=a,let reuired angle is x....
again sine rule in ADC
b/sin(40-x) =a/sin(40+x)..........................(2)
by solving 1&2 we get x=10.
AC=AB MEANS THAT THE ANSWER IS 10.
Correct Sir, Draw a line from A to joining to CB suppose at point E then Angle EAB = 90 deg & EAC = 10 deg. Now Triangles ABC & CAD are Symmetric. So if BC & AD are equal then angle EAC is equal to BCD so it is 10 deg.
I used protractor 10° is correct
angle BCD = 10 degree
I used Protractor !! :D
in tri. ABC:- AB=AC, Ang BAC=100. SO ANGLES (ACB=ABC) ARE EQUALS.
so, ang ACB=ABC={180-100}{2}=40,
Ang CBD=180-40=40
(BC)^{2}=(AB)^{2}+(AC)^{2}
(BC)^{2}=2(AB)^{2}
BC= sqrt{2}AB
BC=AD
AD= sqrt{2}AB
BD=AD-AB= sqrt{2}AB-AB=( sqrt{2}-1)AB
in tri BCD:- (CD)^{2}=(BD)^{2}+(BC)^{2}
(CD)^{2}=( sqrt{2}-1)^{2} (AB)^{2}+2(AB)^{2}
CD=sqrt{5-2*sqrt{2}}AB
FORMULA:- (Sin B)/CD=(Sin C)/BD=(Sin D)/BC
Sin C=(Sin B * BD)/CD=0.18
C=Sin^{-1}(0.18)
Ang BCD=10
from given detailas,,in triangle CAB,with issocellous property ang anle A 100 degree,anle ACB And angle ABC are 40 degree each.So angle CBD is 180 - 40 is 140 degree. Now,extend AD to point E such that BC=BE,with issocellous property angle BEC -angle BCE = 180-140 = 20 degree each.,But BD =AD-AB,so angle BDC =30 and therefore angle BCD =10 degree .Ans.
K.K.GARG,India
How BDC=30 please explain
eqn 1=> sine rule in ACB EQN 2=> sine rule in ACD ON SOLVING ANGLE COME OUT TO BE 10
Here's a pretty solution. Hope I can manage to write it right. I will use the same letters used in the original picture.
We start in the edge AB, and we draw an equilateral triangle faced down, with corners A, B, D. Now we get the measure of BE into the edge BC starting on B, creating the new point F. Since BC/BF = BC/BA = AD/AB, we find that the asked angle is the same as the angle CEF, since the triangle BCE is congruent to the triangle ADC. From the equality BE = BF, and the congruence of ABC and BEF, one can find that the angle BEF measures 40 degrees, therefore, angle AEF measures 20 degrees. Now, AC measures like AE, and angle CAE measures 100 + 60 = 160 degrees. Hence, Angle AEC measures 10 degrees, and therefore, angle CEF measures 20 - 10 = 10 degrees.
Thus, we have that the solution is 10 degrees.
Remark: since I don't know how to add images, I have uploaded one here: http://oi57.tinypic.com/258xnit.jpg . It basically has all the lines I mentioned drawed.
step:1 draw line parallel to AD from C. step:2 Draw line parallel to AC from D. Step:3 Say bot lines intersect at point E. Step:4 Now we have parallelogram ADEC. Step:5 Since AD is parallel to EC; Triangle ACD and AED have same base and between same parallel lines. Therefore, ACB+BCD=AED 40+BCD=50 BCD=10 * * ANSWER
Let E be a point outside △ C A D such that △ C A E is equilateral.
Draw segment B E and notice △ E A B is isosceles ( E A = A B ), with E A ^ B = 1 0 0 ° + 6 0 ° = 1 6 0 ° . Then, A E ^ B = A B ^ E = 1 0 ° .
Now, in △ E C B we will get C E ^ B = 6 0 ° − 1 0 ° = 5 0 °
Notice △ E C B ≅ △ C A D by S A S : E C = C A ; E C ^ B = C A ^ D = 1 0 0 ° ; B C = A D . Because it, A C ^ D = C E ^ B = 5 0 °
We know A C ^ D = 4 0 ° + B C ^ D , so 4 0 ° + B C ^ D = 5 0 ° . Then, B C ^ D = 1 0 °