Tiny Tidy Corner

Without loss of generality let the vertical dimension of the blue square be $2$ and the horizontal dimension $9$ .

Let $P$ be the upper right corner of the blue square, $O$ the center of the circle and $Q$ the point of intersection of the extension of the upper side of the blue square and the vertical diameter of the circle.

Then $\Delta OPQ$ is a right triangle with hypotenuse $|OP| = r$ , the radius of the circle, and side lengths $|OQ| = r - 2$ and $|PQ| = r - 9$ . By Pythagoras, we then have that

$r^{2} = (r - 2)^{2} + (r - 9)^{2} \Longrightarrow r^{2} = r^{2} - 4r + 4 + r^{2} - 18r + 81 \Longrightarrow$

$r^{2} - 22r + 85 = 0 \Longrightarrow (r - 5)(r - 17) = 0$ .

As $r$ must exceed either dimension of the blue square, we conclude that $r = \boxed{17}$ .

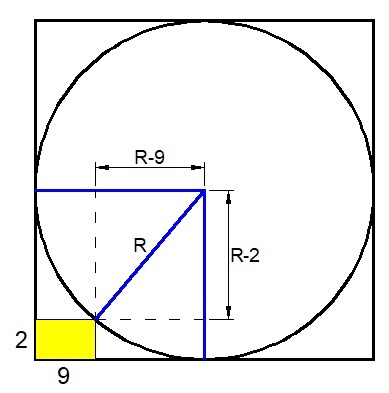Consider the diagram on my left. By Pythagorean theorem, we have

$R^2=(R-9)^2+(R-2)^2$

$R^2=R^2-18R+81+R^2-4R+4$

$R^2-22R+85=0$

By factoring, we have,

$(R-17)(R-5)=0$

$R=17$ or $R=5$

We use $R=17$ because $R=5$ is less than $9$ .