Tipping Point

Identifying the centre of mass of the lamina is the first step: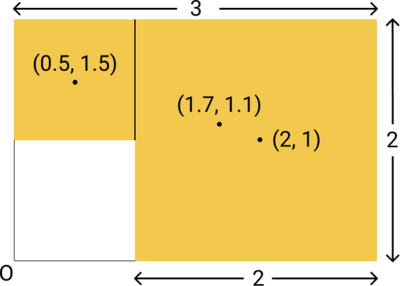 $\overline{x}=\frac{(0.5\times 1) + (2\times 4)}{1+4}=1.7$ and $\overline{y}=\frac{(1.5\times 1) + (1\times 4)}{1+4}=1.1$

At the point of toppling, the centre of mass of the lamina lies vertically above the leftmost pivot point.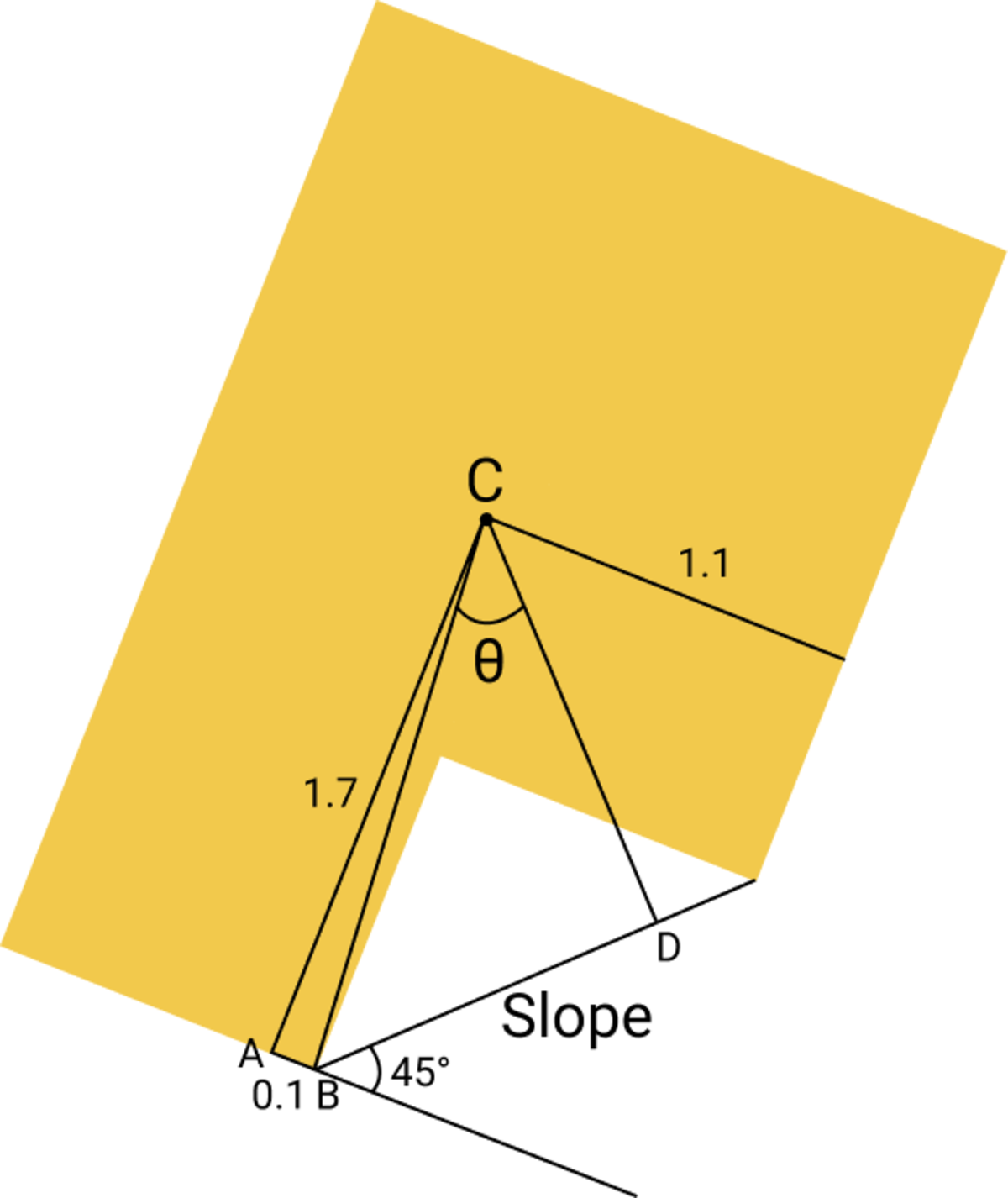

The angle marked $45^\circ$ is equal to $\angle ACD$ .

Having found the centre of mass, we can determine $\angle ACB=\tan^{-1}\left(\frac{0.1}{1.7}\right)\approx 3.37^\circ$ .

$\angle BCD=\theta=\angle ACD - \angle ACB = 45^\circ - 3.37^\circ = 41.6^\circ$ .