Tipping Point

Colored cubes are being stacked on one end of a large block, consisting of seven cubes stuck together, as shown in the picture below.
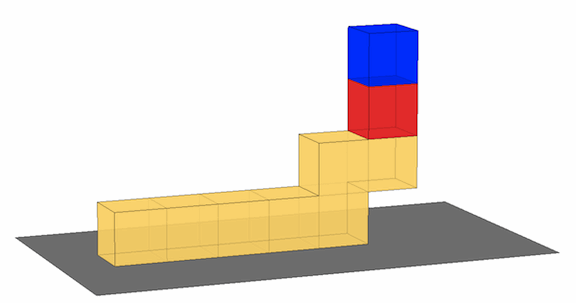
What is the greatest number of blocks you can stack on the end (including the two pictured) without having the whole structure tip over?
Details and assumptions
- The material of all blocks is the same, and of uniform density.
- If the structure is in equilibrium, it will not tip over.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
Let n no.of blocks be stacked,
Let length of each block be a,
As said com must be just near the 5th block,Let it be taken as origin COM of n blocks stacked is at dist of a/2 from origin(along + x), And COM of 5 blocks is at a dist of 5a/2 from origin(along -x) Xcm=0= 2 n m a − 2 2 5 m a so n = 2 5
We apply net torque about the edge of the yellow cube touching the ground as shown

Let the mass of each cube be m
So, τ n e t = 0 ⟹ Σ m g x = Σ m g z ⟹ Σ x = Σ z Here, x is the distance of c.o.m. of the lower cubes.
Now, x varies and z remains constant. So, we get ( 1 + 1 + 3 + 5 + 7 + 9 ) = ( n + 1 ) here n is the number of cubes required.
Thus, we get n = 2 5
The pivot point is going to be the rightmost edge that is in contact with the floor. So you have 6 blocks on the left of the pivot point. One of them is on top of another. Each block has a weight of mg. So we take the net torque on the left side of the pivot point. We pretend that each side of the cube is a length of 1m. The leftmost block has a moment arm of 4.5m. The block to the right of that has a moment arm of 3.5m. The one after that has a moment arm of 2.5m, the one after that has a moment arm of 1.5m, the one after that has a moment arm of .5m. The block on top of the closest block to the pivot point also has a moment arm of .5m. Now we add all the moment arms up and multiply by mg (this is the same as 4.5mg+3.5mg+2.5mg+1.5mg+.5mg+.5mg, which also represents the net torque on the left side). This sums up to 13mg. Now, we notice that since the blocks on the right side of the pivot point are stacked on each other, they will all have the same moment arm of .5m. Now we will call the torque on the right side x mg .5. x represents the number of blocks on the right (including the yellow, red, and blue blocks). We set the torque on the left side of the pivot point equal to the right side torque since they are in equilibrium. 13mg=.5mgx. Solve for x and you get 26. Since the answer doesn't include the yellow block on the right side, you subtract one in order to take that into consideration. 26-1=25.
Assume 1N weight for each block.
- Left side torque.: 1 *(4.5 + 3.5 + 2.5 + 1.5) + 2 * 0.5 = 13
- Right Side torque: (1 + n)*0.5 = 13
=> n =25
i too did like this
The tipping fulcrum point is the right edge at the bottom. Only the bottom row of orange cubes matter since the ''1st floor row' of 2 cubes are arranged symmetrically arranged about this tipping fulcrum point and will not matter. The moment exerted by these ''ground floor 5 orange cubes'' is 5X2.5=12.5 To tip the colored cubes must exert a moment greater than this. The moment arm of the colored cubes is 0.5. If The number of colored cubes N then N X 0.5 >= 12.5 or N>= 25
This , to me is the simplest way. I id the same way,
The block system stays upright as long as the Center of Mass of the system stays above a block that touches the ground. Let x = 0 be the point at which the block line starts (on the left in the figure). Let the cubes be of unit length and unit mass. We will ignore any units. We want the x -coordinate of the Center of Mass to not exceed 5 . If it does, the block will tip over. Let us say we have put n blocks above the snake-system.
Then, the center of mass will be COM x = 7 + n 4 ⋅ 2 + 2 ⋅ 4 . 5 + ( n + 1 ) ⋅ 5 . 5 . And we want COM x ≤ 5 . So we can solve! 7 + n 4 ⋅ 2 + 2 ⋅ 4 . 5 + ( n + 1 ) ⋅ 5 . 5 7 + n 8 + 9 + 2 1 1 ⋅ ( n + 1 ) 7 + n 1 7 + 2 1 1 ⋅ ( n + 1 ) 1 7 + 2 1 1 ⋅ ( n + 1 ) 3 4 + 1 1 ⋅ ( n + 1 ) n ≤ ≤ ≤ ≤ ≤ ≤ 5 5 5 3 5 + 5 n 7 0 + 1 0 n 2 5 . ■
Let n be the number of extra blocks that we stack on the end of the structure. It is clear by logically analyzing the diagram, that, the structure will topple only when the horizontal position of the Center of Mass of the structure is just beyond the 5th Block from the left.
Thus, Assuming the Origin to be at the first block, and the X-axis to be horizontal, Using the definition of Center of Mass and letting the width of each block equal to 2 a for simplicity, we have,
x c m = 7 m + n m m a + m ( 3 a ) + m ( 5 a ) + m ( 7 a ) + 2 ( m ( 9 a ) ) + m ( 1 1 a ) + n ( m ( 1 1 a ) )
Using x c m = 1 0 a by the argument mentioned before, we get,
1 0 a = 7 + n 4 5 + 1 1 n a
⇒ n = 2 5