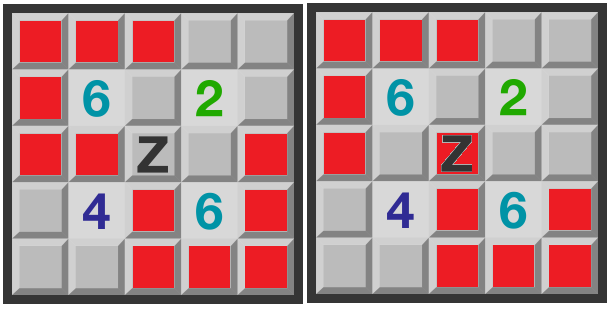
To be a mine or not to be a mine...

Logic Level 1

Is cell Z a mine?

Note : The number in each of the 4 open cells represents the number of hidden mines in the 8 cells around that number.

Yes No There isn't enough information

Zandra Vinegar by Zandra Vinegar

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

9 solutions

Zandra Vinegar Staff
Dec 13, 2017

121 Helpful 0 Interesting 0 Brilliant 1 Confused

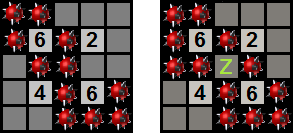
Moderator note:

If the question is instead "is there a configuration of mines consistent with this number pattern?" it becomes what is known as the Minesweeper Consistency Problem.

It's known to be a difficult problem to make a general algorithm for; in computer science jargon, it is NP-complete. Because of this, it is linked to something called the P vs. NP Problem, a problem considered significant enough that the Clay Mathematics Institute has offered a million-dollar prize for its solution.

One way to claim the prize would be to find an efficient algorithm to solve the Minesweeper Consistency Problem (in computer science jargon again, finding a polynomial-time algorithm).

Each number should have eight mine neighbours...

PARITOSH KUMAR - 3 years, 5 months ago

Log in to reply

How do you work that out??

Ben Hunter - 3 years, 5 months ago

What is a mine? Please explain.

Bhanvar Shivpratap Singh Baghel - 3 years, 5 months ago

Log in to reply

Have you played minesweeper before??

Ben Hunter - 3 years, 5 months ago

Not having played minesweeper is your real problem here

Martín Isla - 3 years, 5 months ago

A mine is a hidden bomb, usually underneath the surface of a superficial or some facade of some sort

Rafael Lopez - 3 years, 4 months ago

Although I got it right, it should say that only one mine can be in a cell. Ed Gray

Edwin Gray - 3 years, 5 months ago

Log in to reply

That is a given for the game Minesweeper

Chris Cheek - 3 years, 5 months ago

Log in to reply

You should be aware that not everybody in the world was exposed to the game in their life, so this question could seem a bit irrational to them.

Nathan Pike - 3 years, 5 months ago

Oh yeah I got it

Sandhya Saini - 3 years, 5 months ago

How did you work it out? Basically trial and error?

P P - 3 years, 5 months ago

how ever if this applies to a real situation, it can be concluded that z has a mine. nobody would take the risk to step on that z, in reality or majority people would think that there is a mine. :-)

Renemar Sultones - 3 years, 5 months ago
Zain Majumder
Dec 17, 2017

A red square means that a mine is placed on it. You can see that there is a way for Z Z to have a mine and not have a mine.

98 Helpful 0 Interesting 0 Brilliant 1 Confused

Its a mine

Ben Hunter - 3 years, 5 months ago

The exact same two I had as my examples.

David Richner - 3 years, 5 months ago

I miscounted and tripped myself up. I hope I could have gotten it otherwise...

jem 56 - 3 years, 5 months ago

I feel that as the are numerous ways to arrange the bombs, so tbe above information is false. Also if it showed a hint or a start or a technique it would probably be solved.

STUDY CORNER - 3 years, 5 months ago

Log in to reply

No, there are exactly 3 possible arrangements, one of which is symmetric to the seccond example @Zain Majumder has given, therefore, the above information is true.

On the other hand, I do agree that they could have given some more details about minesweeper rules, or at least provide us with a link.

Marc Garcia - 3 years, 5 months ago
Mevan Alles
Dec 19, 2017

If atleast one combination of mines can be found for which Z is a mine and Z is not a mine, we can conclude information is not enough.

32 Helpful 0 Interesting 0 Brilliant 0 Confused
Robert DeLisle
Dec 20, 2017

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Tthecool Jose
Dec 19, 2017

Just try to find a arrangement where Z is not a mine ; because there are a lot of clearly obvious ways of Z being a mine.

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Tarun Sharma
Dec 19, 2017

The information is not sufficient enough beccause the no of bombs in 8 cells are arbitary so there are infinite ways of arranging the bombs....so there are cases whenre in bomb may be present on z or not

1 Helpful 0 Interesting 0 Brilliant 0 Confused
So Jh
Apr 27, 2018

Answer is C: Probability of Z being a mine because of 6=6/8 Probability of Z being a mine because of 2=2/8 Probability of Z being a mine because of 4=4/8 Probability of Z being a mine because of 6=6/8 Total probability=36/324 Hence we can't be sure

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Nandni Jotwani
Dec 22, 2017

It is possible to find a solution when all the conditions are satisfied but Z is not a mine at the same time we can also obtain a solution where all the conditions are satisfied but Z is a mine .

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Steve Jobs
Dec 22, 2017

Trying a combination that doesn’t include Z as a mine shows that it’s possible for Z not be a mine, and since it’s obvious that Z can be a mine too, it means that there are not enough information

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...